前言
在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。因此多元线性回归比一元线性回归的实用意义更大。
知识储备
常见的回归分析类型:线性回归、0-1回归、定序回归、计数回归和生存回归。这些类型的划分依据是因变量的类型。
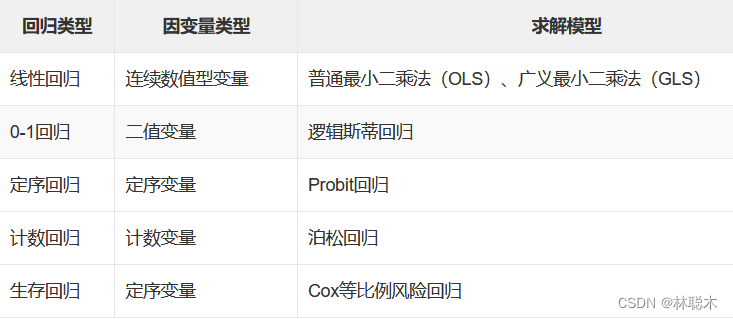
回归分析的任务:通过研究自变量和因变量的相关关系,尝试用自变量来解释因变量的形成机制,从而达到通过自变量去预测因变量的目的。具体如下:
- 判断哪些自变量和因变量是真的相关,而哪些自变量与因变量不相关。
- 判断与因变量相关的自变量的相关关系是正相关还是负相关。
- 对于不同的权重,称为回归系数,用于判断不同自变量对因变量的相对重要性。
数据的分类
- 横截面数据:在某一个时间点收集的不同对象的数据。
- 时间序列数据:对同一对象在不同时间连续观察所取得的数据。
- 面板数据:将横截面数据和时间序列数据综合起来获得的一种数据资源结构。
建模比赛中常考的数据类型:建模比赛中最常用到的是横截面数据和时间序列数据;面板数据更加复杂,属于计量经济学中的模型内容。
<