强化学习数学基础:贝尔曼公式
- 强化学习的数学原理课程总览
- 贝尔曼公式(Bellman Equation)
- 一个示例
- 状态值
- 贝尔曼公式:推导过程
- 贝尔曼公式:矩阵-向量形式(Matrix-vector form)
- 贝尔曼公式:求解状态值
- 动作值(Action value)
- 总结
- 参考资料
强化学习的数学原理课程总览
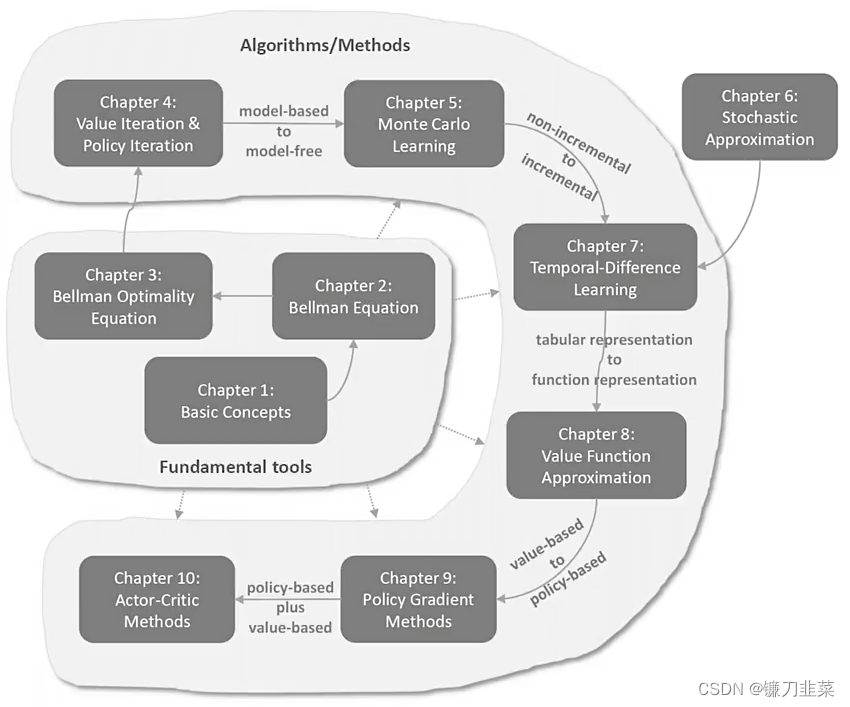
贝尔曼公式(Bellman Equation)
- 一个核心的概念:状态值(
state value) - 一个基础工具:the
Bellman equation
一个示例
**为什么return是重要的?**首先我们根据一个轨迹(trajectory)获得rewards的(discounted)sum。如下所示:
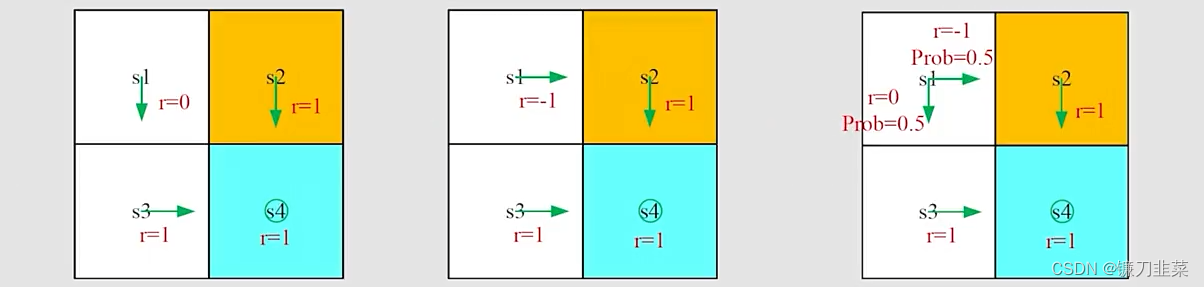
根据上图所示,有两个问题:
-
问题1:从s1点出发,哪种policy是“best”?,哪一个是“worst”?
直观上看,第一个是最优的,第二个是最差的,这是因为第二个经过了forbidden area。 -
问题2:是否可以用数学公式描述这样一种直观感觉?
可以,使用return来评估policies。
基于策略1(左边图),从s1开始,the discounted return计算如下:
r
e
t
u
r
n
1
=
0
+
γ
1
+
γ
2
1
+
.
.
.
=
γ
(
1
+
γ
+
γ
2
+
.
.
.
)
=
γ
1
−
γ
return_1=0+\gamma 1+\gamma ^21+...=\gamma (1+\gamma +\gamma ^2+...)=\frac{\gamma }{1-\gamma }
return1=0+γ1+γ21+...=γ(1+γ+γ2+...)=1−γγ
基于策略2(中间图),从s1开始,the discounted return是:
r
e
t
u
r
n
2
=
−
1
+
γ
1
+
γ
2
1
+
.
.
.
=
−
1
+
γ
(
1
+
γ
+
γ
2
+
.
.
.
)
=
−
1
+
γ
1
−
γ
return_2=-1+\gamma 1+\gamma ^21+...=-1+\gamma (1+\gamma +\gamma ^2+...)=-1+\frac{\gamma }{1-\gamma }
return2=−1+γ1+γ21+...=−1+γ(1+γ+γ2+...)=−1+1−γγ
策略3是随机性的,基于第三个策略(右边图),从s1出发,discounted return是:
r
e
t
u
r
n
3
=
0.5
(
−
1
+
γ
1
−
γ
)
+
0.5
(
γ
1
−
γ
)
=
−
0.5
+
γ
1
−
γ
return_3=0.5(-1+\frac{\gamma }{1-\gamma } )+0.5(\frac{\gamma }{1-\gamma } )=-0.5+\frac{\gamma }{1-\gamma }
return3=0.5(−1+1−γγ)+0.5(1−γγ)=−0.5+1−γγ
基于上面的计算可知,从s1出发, r e t u r n 1 > r e t u r n 3 > r e t u r n 2 return_1>return_3>return_2 return1>return3>return2。因此从结果上看,这是符合之前的直觉的。所以,通过计算return可以评估一个policy的优劣。
那么如何计算return?刚才是用return的定义,现在用一个更好的方法来计算它。以如下图为例:
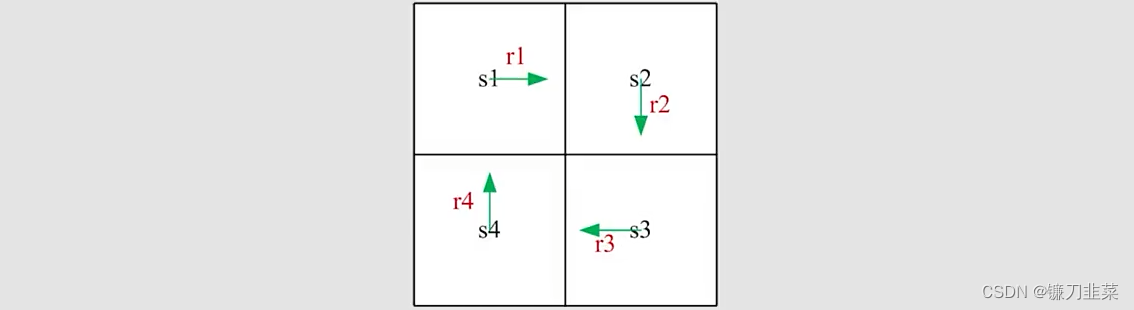
- 方法1:由定义计算,令
v
i
v_i
vi表示从
s
i
(
i
=
1
,
2
,
3
,
4
)
s_i(i=1,2,3,4)
si(i=1,2,3,4)出发得到的return
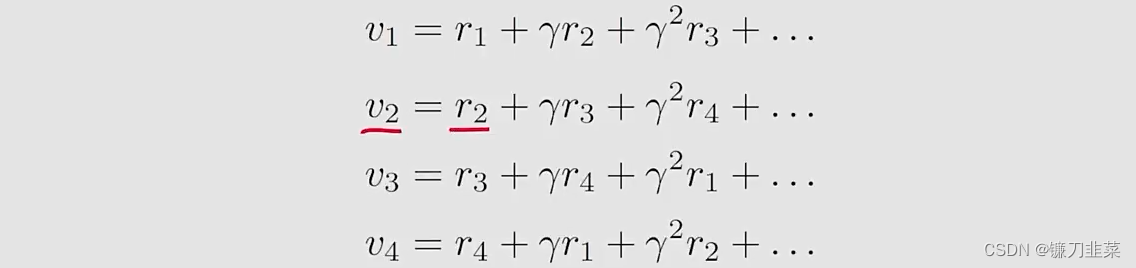
- 方法2:先看下面式子
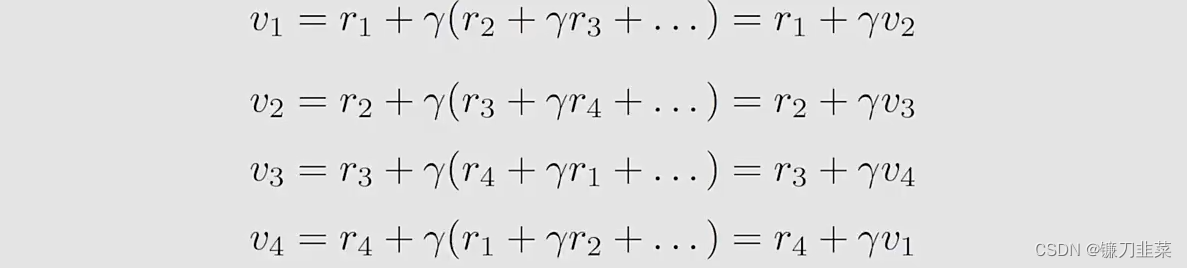
从上面式子中可以得出结论:return依赖于其他状态,这个思想称为Boostrapping。
如何求解这些等式?我们可以将上面的公式写成一个矩阵向量的形式:
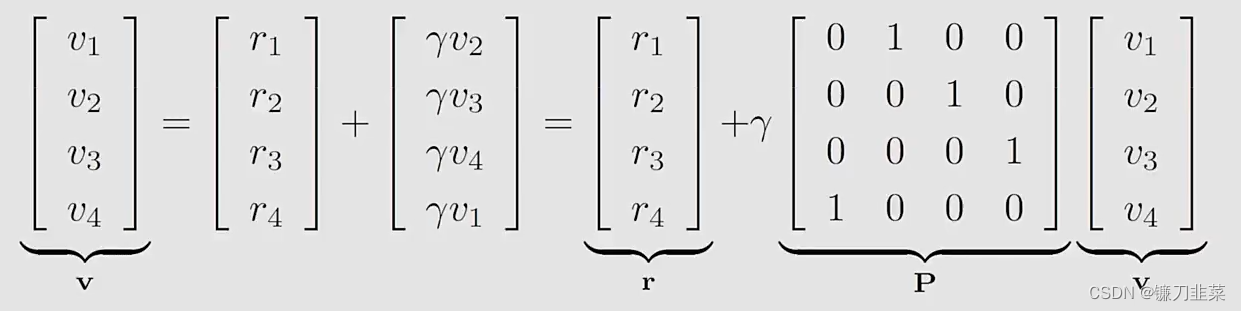
可以写为:
v
=
r
+
γ
P
v
\mathrm{v}=\mathrm{r}+\gamma \mathrm{Pv}
v=r+γPv
这个公式就是一个贝尔曼公式(Bellman equation)(对于这样一个具体的确定性问题):
- 尽管简单,但是它证明一个关键思想:一个状态的值依赖于其他状态的值
- 一个矩阵-向量形式可以更加清晰地知道如何求解状态值。
状态值
首先,定义几个概念。考虑这样一个单步(single-step)的过程:
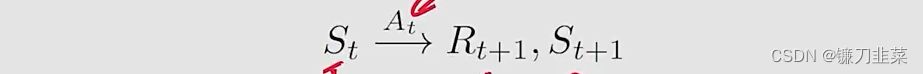
其中:
- t , t + 1 t, t+1 t,t+1:离散时间
- S t S_t St:在时刻 t t t的状态
- A t A_t At:在状态 S t S_t St采取的动作
- R t + 1 R_{t+1} Rt+1:采取动作 A t A_t At之后得到的奖励
- S t + 1 S_{t+1} St+1:采取动作 A t A_t At之后转移到的状态
注意: S t , A t , R t + 1 S_t, A_t, R_{t+1} St,At,Rt+1都是随机变量(random variables)。
根据下面的概率分布决定后续的步骤:
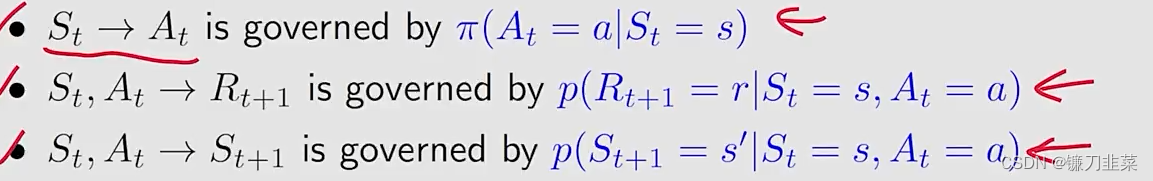
在某一时刻,我们假设我们知道这个模型,即概率分布。
将上面的单步过程推广到一个多步的trajectory上,可以得到:
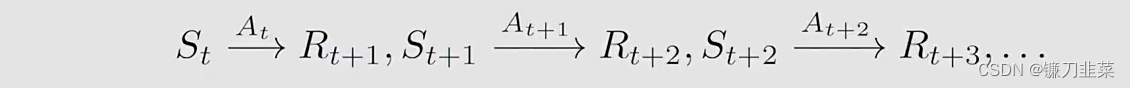
则discounted return计算如下:
G
t
=
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
.
.
.
.
.
.
G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+......
Gt=Rt+1+γRt+2+γ2Rt+3+......
- γ ∈ [ 0 , 1 ) \gamma \in [0,1) γ∈[0,1)是一个折扣率
- G t G_t Gt是一个随机变量,因为 R t + 1 , R t + 2 , . . . R_{t+1},R_{t+2},... Rt+1,Rt+2,...是随机变量。
定义state value:
G
t
G_t
Gt被的期望(或者称为期望值或均值)被定义为state-value function或者简单地称为state value:
v
π
(
s
)
=
E
[
G
t
∣
S
t
=
s
]
v_\pi(s)=\mathbb{E}[G_t|S_t=s]
vπ(s)=E[Gt∣St=s]
注意:
- 它是一个关于s的函数。从不同的s出发,得到的期望也是不同的
- 它是基于策略 π \pi π的,对于不同的策略,state value也可能不同
- 它表示一个状态的“价值”。如果state value比较大,那么这个策略比较好。
问题:return和state value之间有什么关联?
答:state value是从一个state出发得到的所有可能的return的平均值。如果所有——
π
(
a
∣
s
)
,
p
(
r
∣
s
,
a
)
,
p
(
s
′
∣
s
,
a
)
\pi(a|s),p(r|s,a), p(s'|s, a)
π(a∣s),p(r∣s,a),p(s′∣s,a)——是确定行的,则state value与return是相同的。
示例:下面三个图分别对应三个策略:
π
1
,
π
2
,
π
3
\pi_1,\pi_2,\pi_3
π1,π2,π3
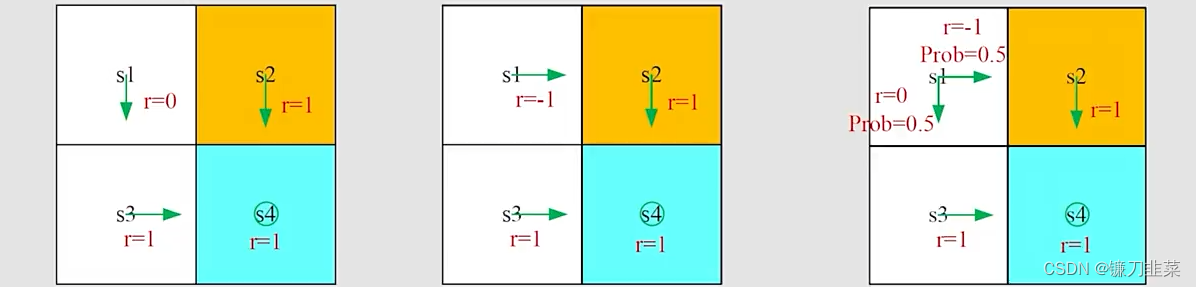
计算从
s
1
s_1
s1开始得到的returns: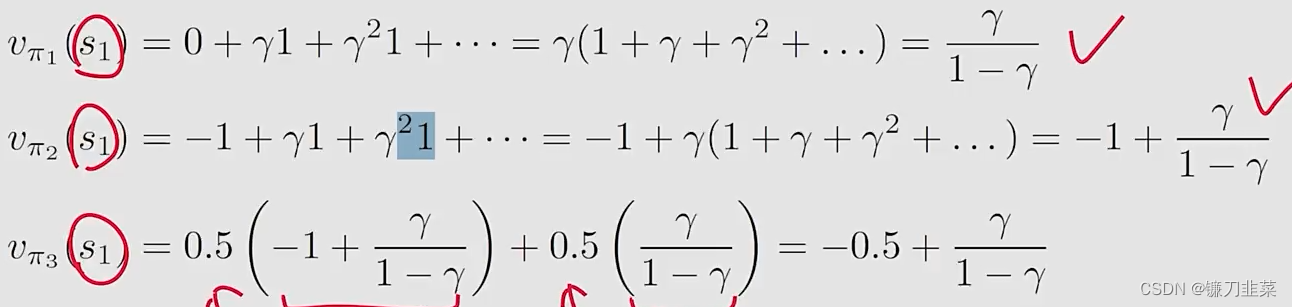
贝尔曼公式:推导过程
用一句话来说,贝尔曼公式用于描述所有不同状态值之间的关系。
考虑一个随机的trajectory:
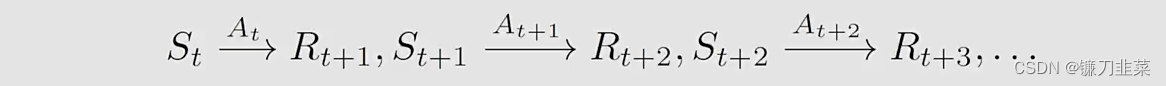
return
G
t
G_t
Gt可以被写为:
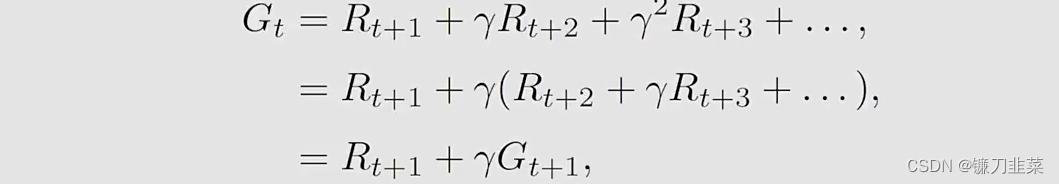
然后,根据state value的定义,用数学形式化:
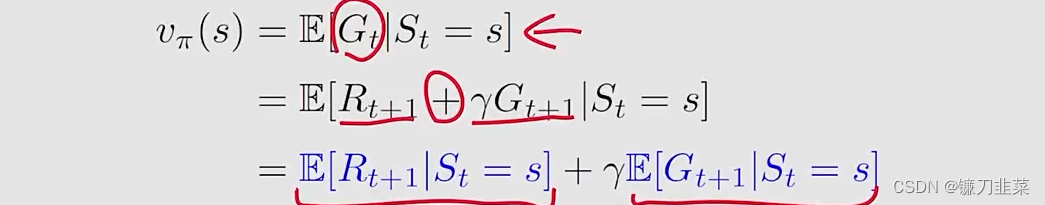
这样就可到了两个部分。然后我们分别计算这两个部分:
首先,计算第一项
E
[
R
t
+
1
∣
S
t
=
s
]
\mathbb{E}[R_{t+1}|S_t=s]
E[Rt+1∣St=s]:
E
[
R
t
+
1
∣
S
t
=
s
]
=
∑
a
π
(
a
∣
s
)
E
[
R
t
+
1
∣
S
t
=
s
,
A
t
=
a
]
=
∑
a
π
(
a
∣
s
)
∑
r
p
(
r
∣
s
,
a
)
r
\mathbb{E}[R_{t+1}|S_t=s]=\sum _a \pi (a|s)\mathbb{E}[R_{t+1}|S_t=s, A_t=a]=\sum _a\pi (a|s)\sum _rp(r|s,a)r
E[Rt+1∣St=s]=a∑π(a∣s)E[Rt+1∣St=s,At=a]=a∑π(a∣s)r∑p(r∣s,a)r
注意:这是得到的一个immediate rewards的均值。
再看第二项
E
[
G
t
+
1
∣
S
t
=
s
]
\mathbb{E}[G_{t+1}|S_t=s]
E[Gt+1∣St=s]:
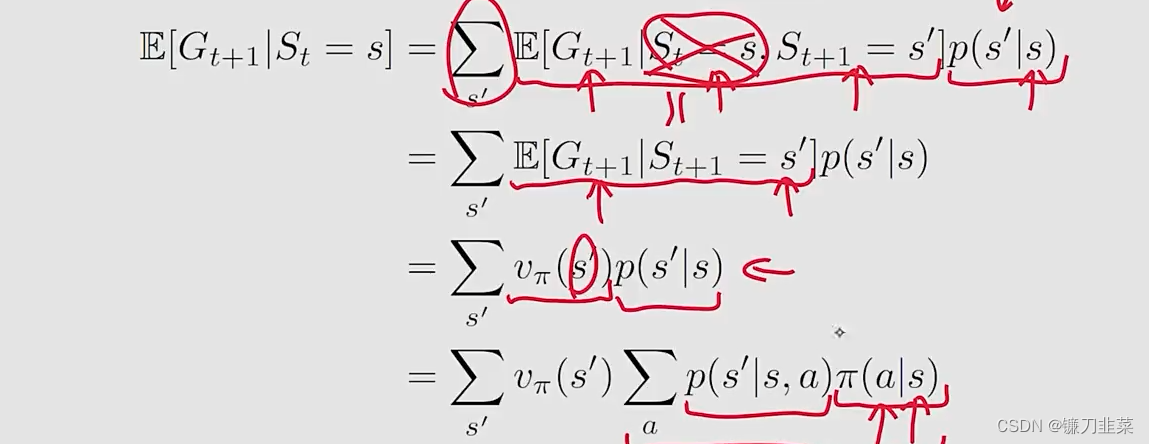
注意:
- 第二项是future reward的均值
- E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] = E [ G t + 1 ∣ S t + 1 = s ′ ] \mathbb{E}[G_{t+1}|S_t=s, S_{t+1}=s']=\mathrm{E}[G_{t+1}|S_{t+1}=s'] E[Gt+1∣St=s,St+1=s′]=E[Gt+1∣St+1=s′]是由于Markov的无记忆功能,即不需要计算状态s的值。
现在,我们有如下公式:

注意:
- 上面的公式成为Bellman equation, 其描述了不同状态的state-value functions之间的关系;
- 它包含两个部分:
the immediate reward term和the future reward term,即当前奖励和未来奖励 - 它是一个等式的集合:所有的state都有这样一个类似的等式。
- v π ( s ) v_\pi(s) vπ(s)和 v π ( s ′ ) v_\pi(s') vπ(s′)是需要被计算的state value,计算方法就是Bootstrapping。
- π ( a ∣ s ) \pi(a|s) π(a∣s)是一个给定的策略policy,求解这个等式就被称为策略评估(policy evaluation)
- p ( r ∣ s , a ) p(r|s,a) p(r∣s,a)和 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a)表示动态模型(dynamic model),分为两种情况,即知道和不知道
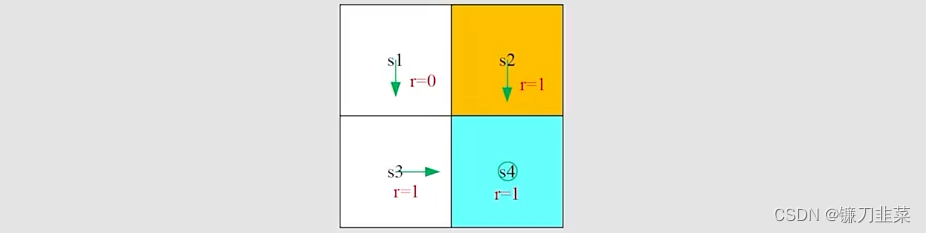
根据上面网格,再次将Bellman公式根据最终的一般形式写出来:
v
π
(
s
)
=
∑
a
π
(
a
∣
s
)
[
∑
r
p
(
r
∣
s
,
a
)
r
+
γ
∑
s
′
p
(
s
′
∣
s
,
a
)
v
π
(
s
′
)
]
v_\pi(s)=\sum _a\pi(a|s)[\sum _rp(r|s,a)r+\gamma \sum _{s'}p(s'|s,a)v_\pi(s')]
vπ(s)=a∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)]
这里非常简单,因为策略是确定性的。
首先,考虑
s
1
s_1
s1的state value:
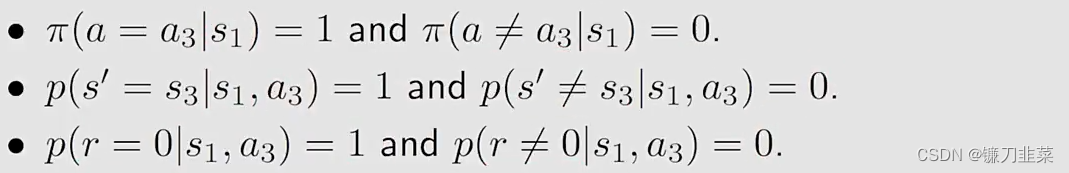
这时候将上述公式的结果提交到贝尔曼公式里边,得到:
v
π
(
s
1
)
=
0
+
γ
v
π
(
s
3
)
v_\pi(s_1)=0+\gamma v_\pi(s_3)
vπ(s1)=0+γvπ(s3)
类似地,我们有如下公式:
v
π
(
s
1
)
=
0
+
γ
v
π
(
s
3
)
v_\pi(s_1)=0+\gamma v_\pi(s_3)
vπ(s1)=0+γvπ(s3)
v
π
(
s
2
)
=
1
+
γ
v
π
(
s
4
)
v_\pi(s_2)=1+\gamma v_\pi(s_4)
vπ(s2)=1+γvπ(s4)
v
π
(
s
3
)
=
1
+
γ
v
π
(
s
4
)
v_\pi(s_3)=1+\gamma v_\pi(s_4)
vπ(s3)=1+γvπ(s4)
v
π
(
s
4
)
=
1
+
γ
v
π
(
s
4
)
v_\pi(s_4)=1+\gamma v_\pi(s_4)
vπ(s4)=1+γvπ(s4)
求解上面等式,通过从最后一个到第一个,逐步求解,得到:
v
π
(
s
4
)
=
1
1
−
γ
v_\pi(s_4)=\frac{1}{1-\gamma }
vπ(s4)=1−γ1
v
π
(
s
3
)
=
1
1
−
γ
v_\pi(s_3)=\frac{1}{1-\gamma }
vπ(s3)=1−γ1
v
π
(
s
2
)
=
1
1
−
γ
v_\pi(s_2)=\frac{1}{1-\gamma }
vπ(s2)=1−γ1
v
π
(
s
1
)
=
γ
1
−
γ
v_\pi(s_1)=\frac{\gamma}{1-\gamma }
vπ(s1)=1−γγ
假设
γ
=
0.9
\gamma=0.9
γ=0.9,带入上面等式中,得到:
v
π
(
s
4
)
=
10
v_\pi(s_4)=10
vπ(s4)=10
v
π
(
s
3
)
=
10
v_\pi(s_3)=10
vπ(s3)=10
v
π
(
s
2
)
=
10
v_\pi(s_2)=10
vπ(s2)=10
v
π
(
s
1
)
=
9
v_\pi(s_1)=9
vπ(s1)=9
当我们计算完成state value之后呢?需要计算action value和改善policy。
练习如下示例:
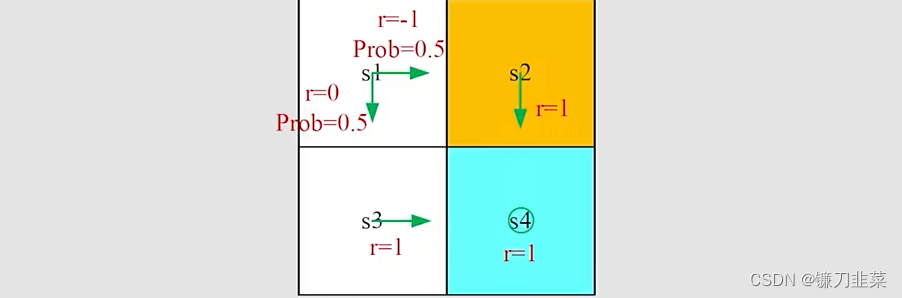
给出一般化的贝尔曼公式:
v
π
(
s
)
=
∑
a
π
(
a
∣
s
)
[
∑
r
p
(
r
∣
s
,
a
)
r
+
γ
∑
s
′
p
(
s
′
∣
s
,
a
)
v
π
(
s
′
)
]
v_\pi(s)=\sum _a\pi(a|s)[\sum _rp(r|s,a)r+\gamma \sum _{s'}p(s'|s,a)v_\pi(s')]
vπ(s)=a∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)]
现在,对于每个state,写出对应的贝尔曼等式,根据上面的贝尔曼公式求解state value,最后比较不同的policy。
对于第一个问题,每个状态的贝尔曼等式如下:
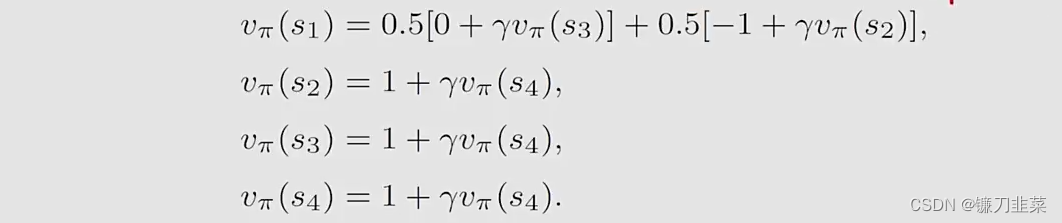
从后往前计算每个state value,有:
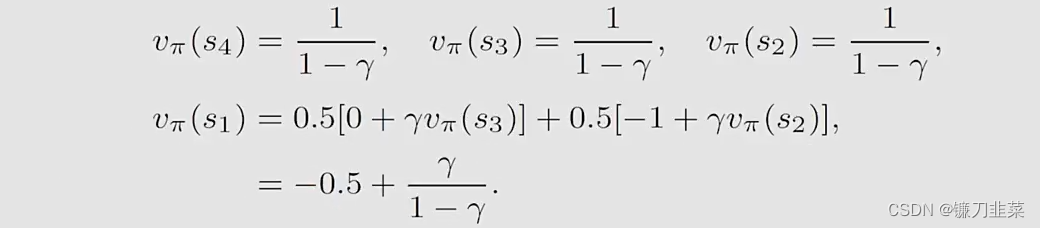
然后,将
γ
=
0.9
\gamma=0.9
γ=0.9带入上面式子中,得到:
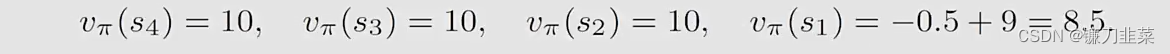
比较不同的策略,这个策略是比较差的,没有之前的策略好。
贝尔曼公式:矩阵-向量形式(Matrix-vector form)
首先考虑如何求解Bellman公式,
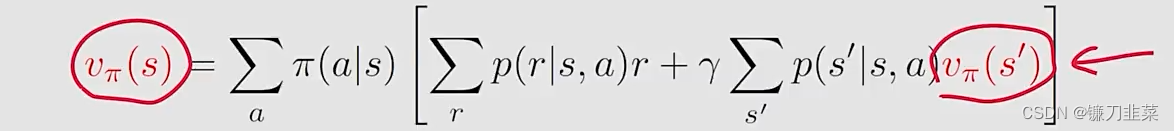
一种unknown依赖于另一种unknown。上面的elementwise form对于每个state
s
∈
S
s\in S
s∈S都是适用的,这意味着将有
∣
S
∣
|S|
∣S∣个类似的公式,如果将这些公式放在一块,将得到一个线性方程组,将它们写为matrix-vector form,这种矩阵-向量形式是优雅而重要(elegant and important)。
Bellman公式的Matrix-vector形式求解如下:
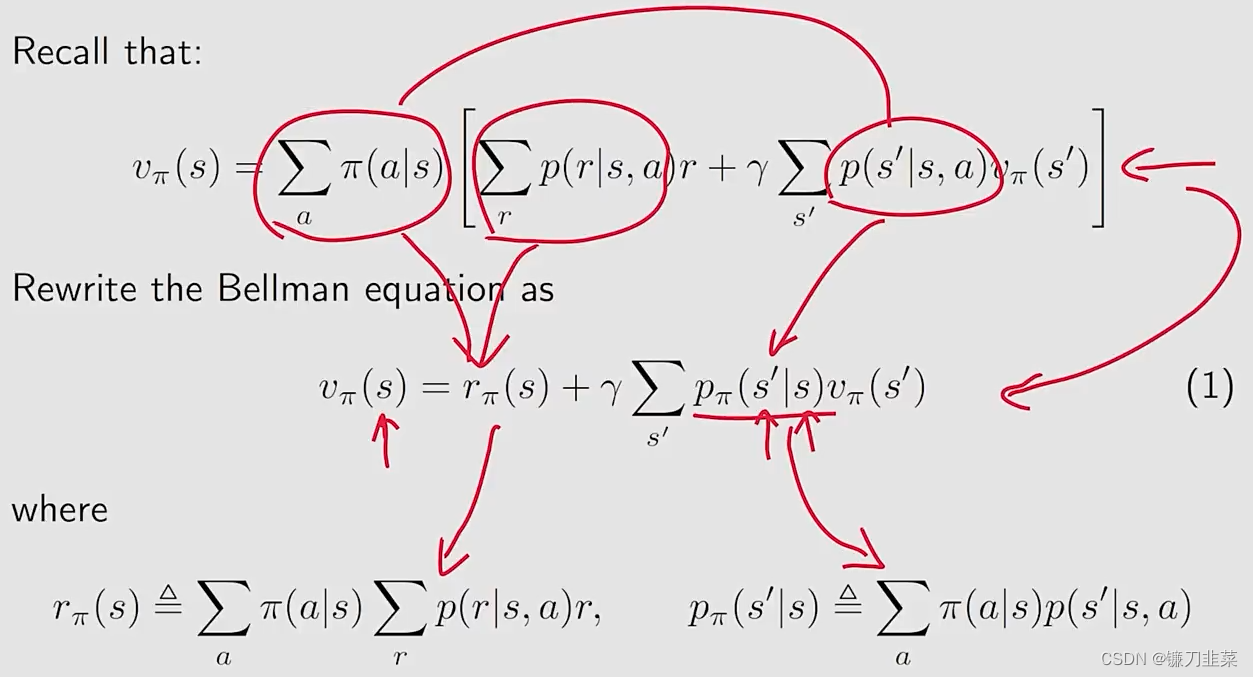
假设states可以索引为
s
i
(
i
=
1
,
.
.
.
,
n
)
s_i(i=1,...,n)
si(i=1,...,n)。对于状态
s
i
s_i
si,Bellman公式是:
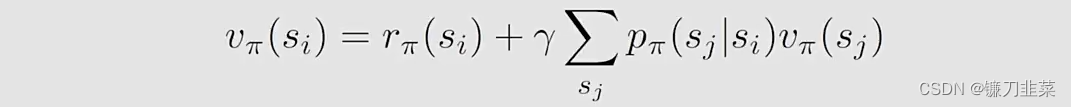
将所有states的这样等式放在一起,用矩阵向量的形式写为:
v
π
=
r
π
+
γ
P
π
v
π
v_\pi=r_\pi+\gamma P_\pi v_\pi
vπ=rπ+γPπvπ
其中:
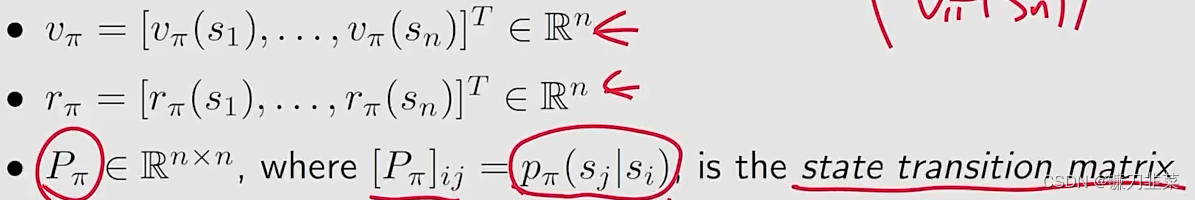
示例如下,假设有4个状态,上面公式可以写为:

进一步地,以网格为例:
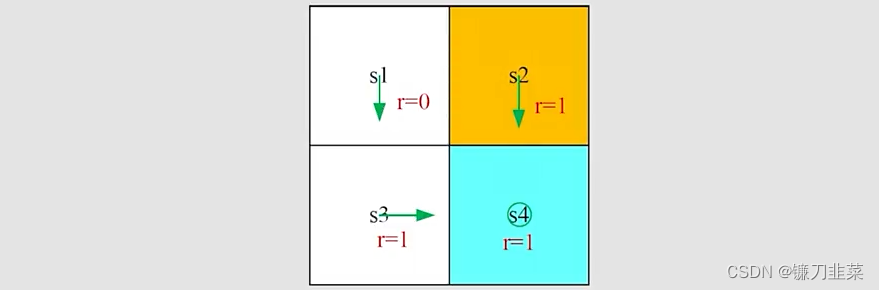
可以写为如下形式:
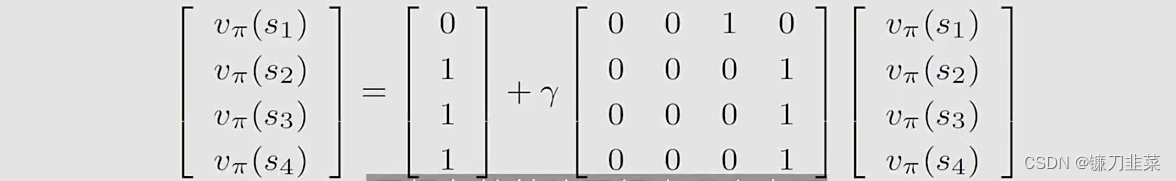
再看一个随机性的网格示例,如下:
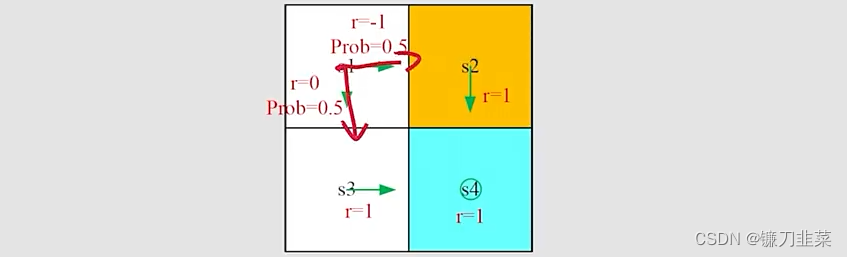
有如下结果:
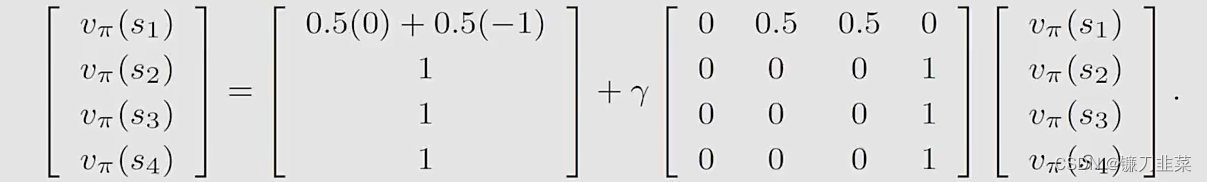
贝尔曼公式:求解状态值
为什么要求解state values?
- 给定一个策略policy,找到对应的state values的过程被称为policy evaluation。这是一个强化学习的基础问题,即找出更好的策略。
- 这对于理解如何求解Bellman公式很重要
如下是Bellman公式的matrix-vector form:
v
π
=
r
π
+
γ
P
π
v
π
v_\pi=r_\pi+\gamma P_\pi v_\pi
vπ=rπ+γPπvπ
其解析表达式(closed-form solution)是
v
π
=
(
I
−
γ
P
π
)
−
1
r
π
v_\pi=(I-\gamma P_\pi)^{-1}r_\pi
vπ=(I−γPπ)−1rπ,实际上,我们仍然需要使用数值工具计算矩阵的逆。
因此,在实际中,我们使用迭代算法去求解(iterative solution):
v
k
+
1
=
r
π
+
γ
P
π
v
k
v_{k+1}=r_\pi +\gamma P_\pi v_k
vk+1=rπ+γPπvk,这样的算法将得到一个序列
{
v
0
,
v
1
,
v
2
,
.
.
.
}
\{v_0,v_1,v_2,...\}
{v0,v1,v2,...},如下:
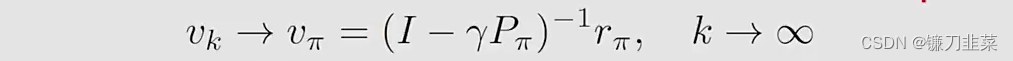
当k趋近于无穷的时候,则
v
k
v_k
vk就趋近于
v
π
v_\pi
vπ。证明如下:

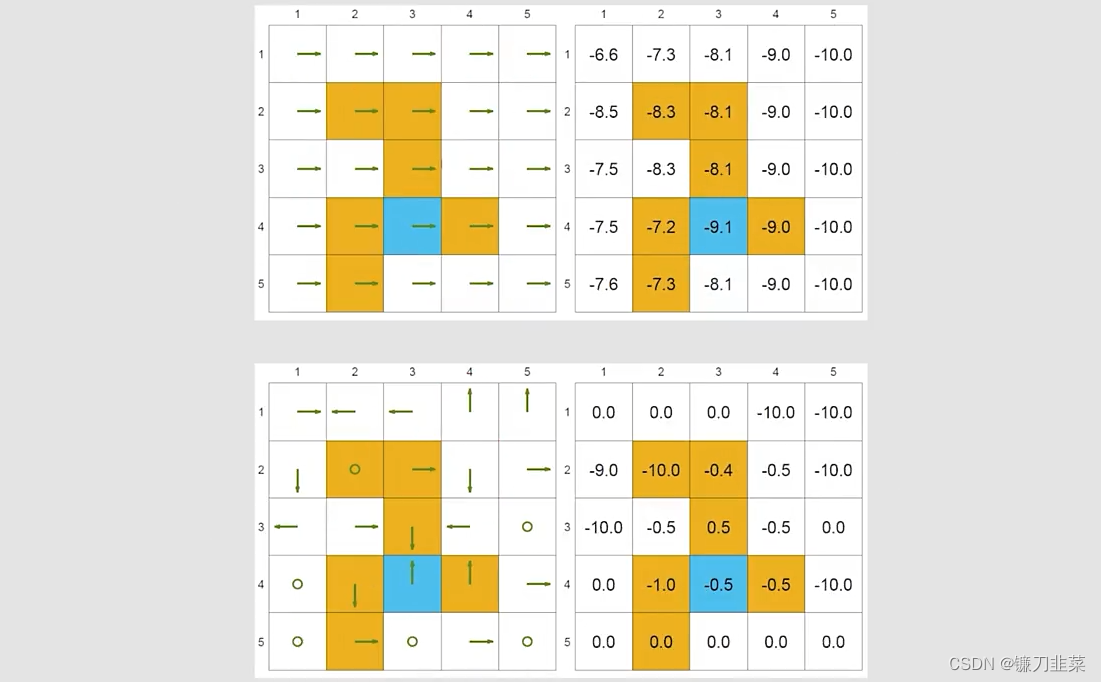
示例:
r
b
o
u
n
d
a
r
y
=
r
f
o
r
b
i
d
d
e
n
=
−
1
,
r
t
a
r
g
e
t
=
+
1
,
γ
=
0.9
r_{boundary}=r_{forbidden}=-1,r_{target}=+1, \gamma=0.9
rboundary=rforbidden=−1,rtarget=+1,γ=0.9,下面是两个”bad“策略和状态值。the state value不如好的policies。
动作值(Action value)
state value和action value的区别:
- State value: 智能体starting from a state得到的平均return
- Action value:智能体starting from a state并taking an action得到的平均return
通过action value,可以得到哪个action是更好的。
Action value的定义:
q
π
(
s
,
a
)
=
E
[
G
t
∣
S
t
=
s
,
A
t
=
a
]
q_\pi(s,a)=\mathbb{E}[G_t|S_t=s, A_t=a]
qπ(s,a)=E[Gt∣St=s,At=a],其中
q
π
(
s
,
a
)
q_\pi(s,a)
qπ(s,a)是state-action pair
(
s
,
a
)
(s,a)
(s,a)的函数,
q
π
(
s
,
a
)
q_\pi(s,a)
qπ(s,a)依赖于
π
\pi
π。
于是,基于条件期望的性质,可以有:
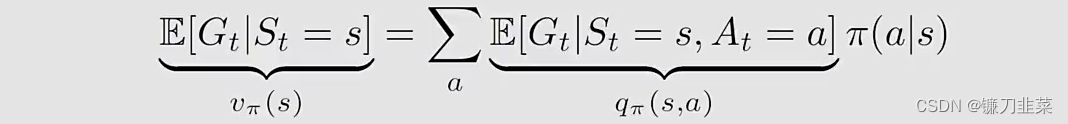
因此,可以将上面式子写为:
v
π
(
s
)
=
∑
a
π
(
a
∣
s
)
q
π
(
s
,
a
)
v_\pi (s)=\sum_a\pi(a|s)q_\pi(s,a)
vπ(s)=a∑π(a∣s)qπ(s,a)
回顾之前的state value公式:
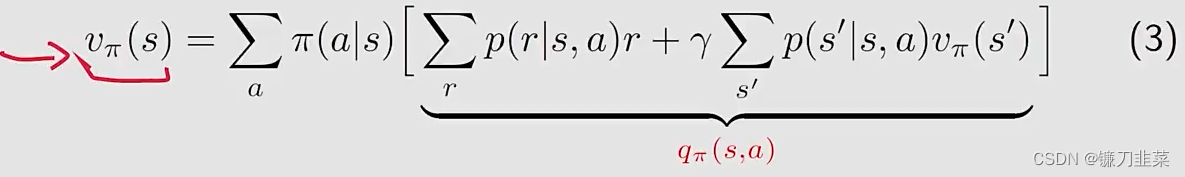
可以得到action-value函数如下:
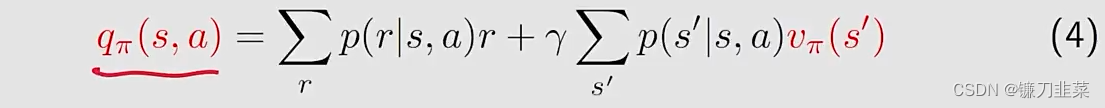
示例:
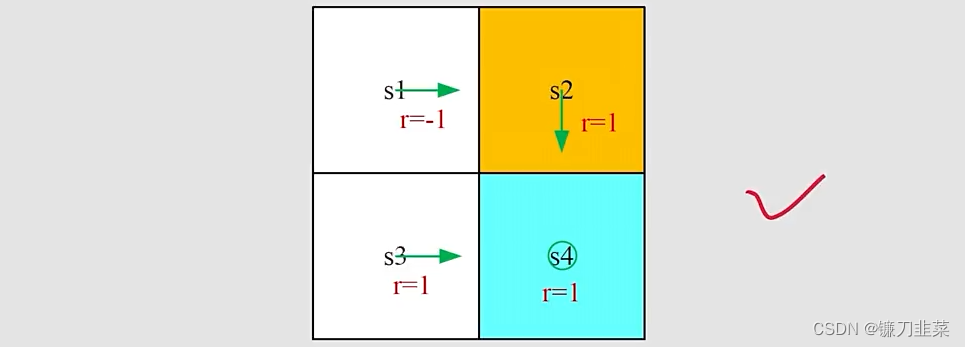
针对
s
1
s_1
s1写出action value:
q
π
(
s
1
,
a
2
)
=
−
1
+
γ
v
π
(
s
2
)
q_\pi (s_1, a_2)=-1+\gamma v_\pi (s_2)
qπ(s1,a2)=−1+γvπ(s2)
除了采取a2动作之外,还可以采取a1, a3, a4动作,那么它们的action value是多少呢?
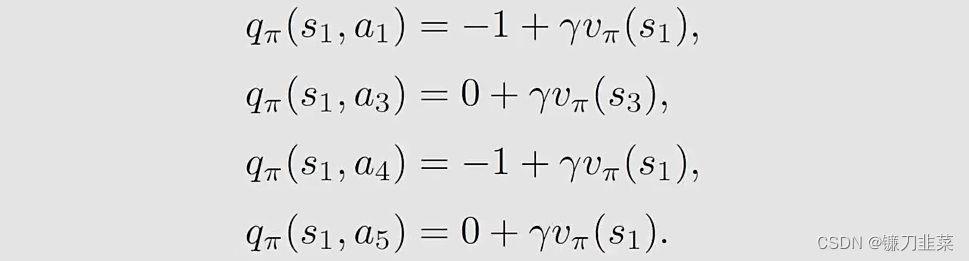
总的来说
- Action value是非常重要的,因为我们关注哪一种action会被采用;
- 我们可以首先计算所有的state value,然后计算action value;
- can also directly calculate the action values with or without models.
总结
关键概念:
-
State value: v π ( s ) = E [ G t ∣ S t = s ] v_\pi (s)=\mathbb{E}[G_t|S_t=s] vπ(s)=E[Gt∣St=s]
-
Action value: q π ( s , a ) = E [ G t ∣ S t = s , A t = a ] q_\pi (s,a)=\mathbb{E}[G_t|S_t=s, A_t=a] qπ(s,a)=E[Gt∣St=s,At=a]
-
贝尔曼公式(elementwise form):
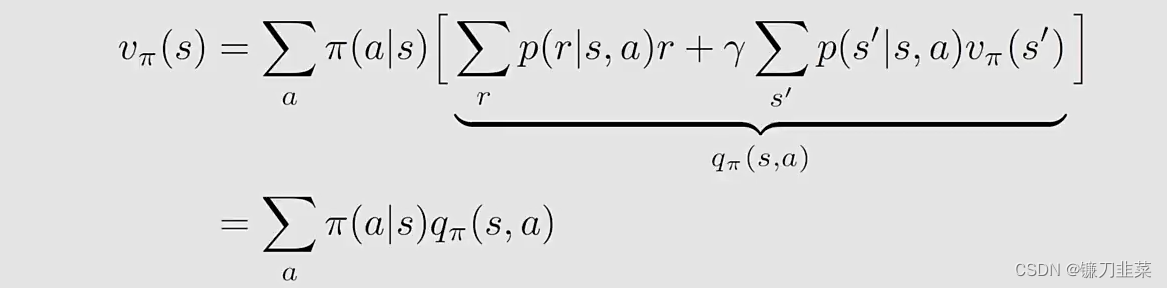
-
贝尔曼公式(matrix-vector form): v π = r π + γ P π v π v_\pi=r_\pi+\gamma P_\pi v_\pi vπ=rπ+γPπvπ
-
如何求解贝尔曼公式:解析法(closed-form solution),迭代法(iterative solution)
参考资料
[1] 《强化学习的数学原理》赵世钰教授 西湖大学工学院
[2] 《动手学强化学习》 俞勇著







![数据结构与算法之[把数字翻译成字符串]动态规划](https://img-blog.csdnimg.cn/img_convert/619808a6dc64103a387a206898673c98.png)