目录
1. 整数反转
2. 求最大公约数和最小公倍数
最大公约数
最小公倍数
3. 单词搜索 II
附录:
DFS 深度优先搜索算法
BFS 广度优先搜索算法
BFS 和 DFS 的区别
1. 整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−2^31, 2^31 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
输入:x = 123 输出:321
示例 2:
输入:x = -123 输出:-321
示例 3:
输入:x = 120 输出:21
示例 4:
输入:x = 0 输出:0
提示:
-2^31 <= x <= 2^31 - 1
代码:
import math
class Solution:
def reverse(self, x: int) -> int:
r = 0
y = 0
abs_x = abs(x)
negative = x < 0
while abs_x != 0:
r = abs_x % 10
y = y*10+r
abs_x = int(math.floor(abs_x/10))
if negative:
y = -y
return 0 if (y > 2147483647 or y < -2147483648) else y
s = Solution()
nums = [123, -123, 120, 0, 1234567809]
for x in nums:
print(s.reverse(x))优化后的代码:
class Solution:
def reverse(self, x: int) -> int:
num, neg = 0, x<0
if neg: x *= -1
while x:
num = num*10 + x%10
x //= 10
res = -num if neg else num
return res if -2**31<=res<2**31 else 0
s = Solution()
nums = [123, -123, 120, 0, 1234567809]
for x in nums:
print(s.reverse(x))代码2: python 数和字串的转换非常方便,负数考虑负号。
class Solution(object):
def reverse(self, x:int)->int:
res = (-1 if x<0 else 1)*int(str(abs(x))[::-1])
return res if -2**31<=res<2**31 else 0
s = Solution()
nums = [123, -123, 120, 0, 1234567809]
for x in nums:
print(s.reverse(x))代码3: 负号还可以用 x//abs(x) 来求,但要排队div by 0。
class Solution(object):
def reverse(self, x:int)->int:
res = abs(x)//x*int(str(abs(x))[::-1]) if x else 0
return res if -2**31<=res<2**31 else 0
s = Solution()
nums = [123, -123, 120, 0, 1234567809]
for x in nums:
print(s.reverse(x))2. 求最大公约数和最小公倍数
输入两个数x 和y,如果x 或y 小于等于0,提示请输入正整数,求这两个数的最大公约数和最小公倍数。
注意:可以采用欧几里得辗转相除算法来求最大公约数。最小公倍数的计算方法是两数的乘积除以两数最大公约数的结果。
x = int(input("输入x:"))
y = int(input("输入y:"))
if x <= 0 or y <= 0:
print("请输入正整数")
if x < y:
x,y = y,x
v1 = x*y
v2 = x%y
while v2 != 0:
x = y
y = v2
v2 = x % y
v1 =v1 // y
print("最大公约数为:%d" % y)
print("最小公倍数为:%d" % v1) 最大公约数
方法一:for循环
def GCD(m, n):
gcd = 1 # 此行可以省略
for i in range(1,min(m, n)+1):
if m%i==0 and n%i==0:
gcd = i
return gcd
print(GCD(81,3))
print(GCD(81,15))
print(GCD(81,54))方法二:while循环
def GCD(m, n):
while m!=n:
if m>n: m -= n
else: n -= m
return m
print(GCD(81,3))
print(GCD(81,15))
print(GCD(81,54))方法三:递归法
def GCD(m, n):
if n==0: return m
return GCD(n, m%n)
print(GCD(81,3))
print(GCD(81,15))
print(GCD(81,54))方法四:辗转相除法
def GCD(m, n):
while n!=0:
m, n = n, m%n
return m
print(GCD(81,3))
print(GCD(81,15))
print(GCD(81,54))方法五:递减法
def GCD(m, n):
gcd = min(m, n)
while m%gcd or n%gcd:
gcd -= 1
return gcd
print(GCD(81,3))
print(GCD(81,15))
print(GCD(81,54))方法六:库函数math.gcd
from math import gcd
print(gcd(81,3))
print(gcd(81,15))
print(gcd(81,54))或者:直接用 __import__('math').gcd
__import__('math').gcd(81,3)
__import__('math').gcd(81,15)
__import__('math').gcd(81,54)方法七:约分法,库函数fractions.Fraction()
def GCD(m, n):
from fractions import Fraction
return m//Fraction(m, n).numerator #取分子
#return n//Fraction(m, n).denominator #或取分母
print(GCD(81,3))
print(GCD(81,15))
print(GCD(81,54))最小公倍数
方法一:循环暴力法
def LCM(m, n):
for i in range(max(m,n),m*n+1):
if i%m==0 and i%n==0:
return i
print(LCM(81,3))
print(LCM(81,15))
print(LCM(81,54))方法二:与最大公约数的关系
最小公倍数LCM 与 最大公约数GCD的关系: m * n = LCM(m, n) * GCD(m, n)
对应最大公约数的几种方法,返回 m*n 整除 GCD(m,n) 即可。
3. 单词搜索 II
给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表 words,找出所有同时在二维网格和字典中出现的单词。
单词必须按照字母顺序,通过 相邻的单元格 内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。
示例 1:
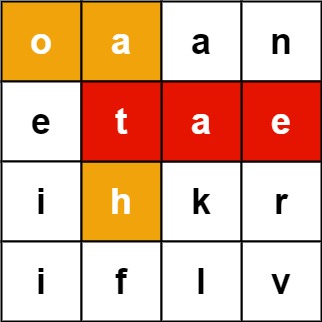
输入:board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"] 输出:["eat","oath"]
示例 2:
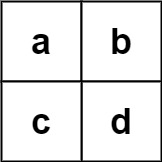
输入:board = [["a","b"],["c","d"]], words = ["abcb"] 输出:[]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 12board[i][j]是一个小写英文字母1 <= words.length <= 3 * 1041 <= words[i].length <= 10words[i]由小写英文字母组成words中的所有字符串互不相同
class Solution:
def findWords(self, board: list, words: list) -> list:
if not board or not board[0] or not words:
return []
self.root = {}
for word in words:
node = self.root
for char in word:
if char not in node:
node[char] = {}
node = node[char]
node["#"] = word
res = []
for i in range(len(board)):
for j in range(len(board[0])):
tmp_state = []
self.dfs(i, j, board, tmp_state, self.root, res)
return res
def dfs(self, i, j, board, tmp_state, node, res):
if "#" in node and node["#"] not in res:
res.append(node["#"])
if [i, j] not in tmp_state and board[i][j] in node:
tmp = tmp_state + [[i, j]]
candidate = []
if i - 1 >= 0:
candidate.append([i - 1, j])
if i + 1 < len(board):
candidate.append([i + 1, j])
if j - 1 >= 0:
candidate.append([i, j - 1])
if j + 1 < len(board[0]):
candidate.append([i, j + 1])
node = node[board[i][j]]
if "#" in node and node["#"] not in res:
res.append(node["#"])
for item in candidate:
self.dfs(item[0], item[1], board, tmp, node, res)
if __name__ == '__main__':
s = Solution()
board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]]
words = ["oath","pea","eat","rain"]
print(s.findWords(board, words))
board = [["a","b"],["c","d"]]
words = ["abcb"]
print(s.findWords(board, words))
输出:
['oath', 'eat']
[]
附录:
DFS 深度优先搜索算法
Depth-First-Search,是一种用于遍历或搜索树或图的算法。这个算法会尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
BFS 广度优先搜索算法
Breadth-First Search,又译作宽度优先搜索,或横向优先搜索,是一种图形搜索算法。简单的说,BFS是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。
BFS 和 DFS 的区别
1 数据结构
bfs 遍历节点是先进先出,一般使用队列作为辅助数据结构
dfs遍历节点是先进后出,一般使用栈作为辅助数据结构
2 访问节点的方式
bfs是按层次访问的,先访问源点,再访问它的所有相邻节点,并且标记结点已访问,根据每个邻居结点的访问顺序,依次访问它们的邻居结点,并且标记节点已访问,重复这个过程,一直访问到目标节点或无未访问的节点为止。
dfs 是按照一个路径一直访问到底,当前节点没有未访问的邻居节点时,然后回溯到上一个节点,不断的尝试,直到访问到目标节点或所有节点都已访问。
3 应用
bfs 适用于求源点与目标节点距离近的情况,例如:求最短路径。
dfs 更适合于求解一个任意符合方案中的一个或者遍历所有情况,例如:全排列、拓扑排序、求到达某一点的任意一条路径。





![数据结构与算法之[把数字翻译成字符串]动态规划](https://img-blog.csdnimg.cn/img_convert/619808a6dc64103a387a206898673c98.png)