三、线性神经网络
3.1 线性回归
3.1.1 介绍
1. 回归是为一个或多个自变量与因变量之间的关系建模的一类方法。而线性回归基于几个简单的假设:① 自变量和因变量关系是线性的;② 允许包含噪声但是噪声遵循正态分布。
2. 训练数据集/训练集,样本/数据点/数据样本,标签/目标(试图预测的目标),特征/协变量(预测所依据的自变量)的概念,用
n
n
n 来表示数据集中的样本数,对索引为
i
i
i 的样本,输入表示为
x
(
i
)
=
[
x
1
(
i
)
,
x
2
(
i
)
]
⊤
\mathbf{x}^{(i)}=[x_1^{(i)}, x_2^{(i)}]^{\top}
x(i)=[x1(i),x2(i)]⊤,对应的标签为
y
(
i
)
y^{(i)}
y(i)。
3. 线性假设中包含权重和偏置,是对输入特征的一个仿射变换。将所有特征放到向量
w
∈
R
d
\mathbf{w}\in\mathbb{R}^d
w∈Rd 中,得到线性模型的简洁表示:
y
^
=
w
⊤
x
+
b
\hat{y}=\mathbf{w}^{\top}\mathbf{x}+b
y^=w⊤x+b,进而得到整个数据集的模型表示:
y
^
=
X
w
+
b
\hat{y}=\mathbf{Xw}+b
y^=Xw+b,要得到最好的模型参数
w
\mathbf{w}
w 和
b
b
b ,还需要两个东西:
(1)一种模型质量的度量方式——损失函数
L
(
w
,
b
)
=
1
n
∑
i
=
1
n
l
(
i
)
(
w
,
b
)
=
1
n
∑
i
=
1
n
1
2
(
w
⊤
x
(
i
)
+
b
−
y
(
i
)
)
2
(1)
L(\mathbf{w},b)=\frac{1}{n}\sum^n_{i=1}l^{(i)}(\mathbf{w},b)=\frac{1}{n}\sum^n_{i=1}\frac{1}{2}(\mathbf{w}^{\top}\mathbf{x}^{(i)}+b-y^{(i)})^2\tag{1}
L(w,b)=n1i=1∑nl(i)(w,b)=n1i=1∑n21(w⊤x(i)+b−y(i))2(1)
w
∗
,
b
∗
=
arg min
w
,
b
L
(
w
,
b
)
(2)
\mathbf{w}^*,b^*=\argmin_{\mathbf{w},b}L(\mathbf{w},b)\tag{2}
w∗,b∗=w,bargminL(w,b)(2)
线性回归的解可以用一个公式简单表达出来,但这种方法对问题限制很严格,因此无法广泛应用于深度学习,于是就需要下面的——
(2)一种能够更新模型以提高模型预测质量的方法。如梯度下降法(Gradient Descent),可以计算损失函数关于模型参数的导数,而实际执行时通常是在每次需要计算更新的时候随机抽取一小批样本,这种变体称为:小批量随机梯度下降。
随机抽取一个小批量
B
\mathcal{B}
B,预先确定一个正数
η
\eta
η,下面是更新过程:
(
w
,
b
)
←
(
w
,
b
)
−
η
∣
B
∣
∑
i
∈
B
∂
(
w
,
b
)
l
(
i
)
(
w
,
b
)
(3)
(\mathbf{w},b)\leftarrow(\mathbf{w},b)-\frac{\eta}{\vert\mathcal{B}\vert}\sum_{i\in\mathcal{B}}\partial_{(\mathbf{w},b)}l^{(i)}(\mathbf{w},b)\tag{3}
(w,b)←(w,b)−∣B∣ηi∈B∑∂(w,b)l(i)(w,b)(3)
其中
∣
B
∣
\vert\mathcal{B}\vert
∣B∣ 表示每个小批量中的样本数,也称为批量大小(batch size),
η
\eta
η 表示学习率,它们通过预先手动设定,这些可以调节但是不再训练过程中更新的参数称为超参数。
4. 泛化的挑战;用模型进行预测;
5. 矢量化加速:在训练模型时,对计算进行矢量化,从而利用线性代数库,而非开销高昂的Python For循环,缩减程序运行所需时间。
6. 正态分布与平方损失:考虑观测信息中的噪声并设定其服从正态分布后,有
y
=
w
⊤
x
+
b
+
ϵ
y=\mathbf{w^\top x}+b+\epsilon
y=w⊤x+b+ϵ,其中
ϵ
∼
N
(
0
,
σ
2
)
\epsilon\sim\mathcal{N}(0,\sigma^2)
ϵ∼N(0,σ2),极大似然估计…
7. 从线性回归到深度网络:神经网络涵盖了丰富的模型,可以使用描述神经网络的方式描述线性模型,下面用“层”符号重写这个模型。(注意:下图中隐去了权重和偏置的值)

线性回归是一个单层神经网络
对于线性回归,每个输入都与输出相连,这种变换被称为全连接层(fully-connected layer)或稠密层(dense layer)。这些算法的想法一定程度上归功于我们对真实生物神经系统的研究。
3.1.2 线性回归的从零开始实现
3.1.3 线性回归的简洁实现
3.2 softmax回归
3.2.1 介绍
1. [分类问题] 回归可以用于预测多少的问题,而我们也可能对分类问题感兴趣,不是问“多少”,而是问“哪一个”。有两种差别微妙的问题:① 只区分“硬性”类别;② 得到“软性”类别,即属于每个类别的概率。
2. [独热编码] 统计学家很早以前就发明了一种表示分类数据的简单方法:独热编码,它是一个向量,分量与类别一样多,由此,标签
y
y
y可以表示为:
y
∈
{
(
1
,
0
,
0
)
,
(
0
,
1
,
0
)
,
(
0
,
0
,
1
)
}
y\in\{(1,0,0),(0,1,0),(0,0,1)\}
y∈{(1,0,0),(0,1,0),(0,0,1)}。
3. [多输出模型] 以4像素图片区分三种类别为例,为估计每个类别概率,需要一个多输出模型:
o
1
=
x
1
w
11
+
x
2
w
12
+
x
3
w
13
+
x
4
w
14
+
b
1
o
2
=
x
1
w
21
+
x
2
w
22
+
x
3
w
23
+
x
4
w
24
+
b
2
o
3
=
x
1
w
31
+
x
2
w
32
+
x
3
w
33
+
x
4
w
14
+
b
3
(4)
o_1=x_1w_{11}+x_2w_{12}+x_3w_{13}+x_4w_{14}+b_1\\ o_2=x_1w_{21}+x_2w_{22}+x_3w_{23}+x_4w_{24}+b_2\\ o_3=x_1w_{31}+x_2w_{32}+x_3w_{33}+x_4w_{14}+b_3\tag{4}
o1=x1w11+x2w12+x3w13+x4w14+b1o2=x1w21+x2w22+x3w23+x4w24+b2o3=x1w31+x2w32+x3w33+x4w14+b3(4)
使用神经网络图描述如下,可以看到softmax回归也是一个单层神经网络,输出层也是全连接层
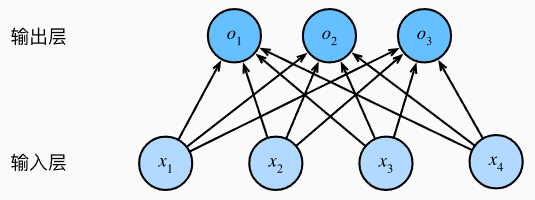
softmax回归是一个单层神经网络
4. [参数开销]深度学习中,全连接层无处不在,对于任何具有 d d d 个输入和 q q q 个输出的全连接层,参数开销为 O ( d q ) \mathcal{O}(dq) O(dq) ,这在实践中可能是不可接受的,这个成本可以减少到 O ( d q n ) \mathcal{O}(\frac{dq}{n}) O(ndq),超参数 n n n 可以灵活指定,以平衡参数节约与模型有效性(Zhang et al., 2021)。
5. [softmax函数]如果要将输出视为概率,必须保证任何数据上的输出都非负且总和为1。softmax函数能够将未规范化的预测转换为非负数且总和为1,同时保持模型可导性质,公式如下:
y
^
=
softmax
(
o
)
其中
y
^
j
=
exp
(
o
j
)
∑
k
exp
(
o
k
)
(5)
\hat{\mathbf{y}}=\text{softmax}(\mathbf{o})\ \ \ \ 其中\ \ \ \ \hat{y}_j=\frac{\exp(o_j)}{{\sum}_k\exp(o_k)}\tag{5}
y^=softmax(o) 其中 y^j=∑kexp(ok)exp(oj)(5)
这个过程中仍然保持
arg max
j
y
^
j
=
arg max
j
o
j
\argmax_j\hat{y}_j=\argmax_jo_j
argmaxjy^j=argmaxjoj,虽然softmax非线性,但是softmax回归的输出仍然由输入特征的仿射变换决定,因此softmax回归是一个线性模型。
6. [小批量的矢量化],加快
X
\mathbf{X}
X 和
W
\mathbf{W}
W 的矩阵向量乘法。
7. [损失函数],softmax函数给出了一个向量
y
^
\hat{y}
y^,即“对给定输入
x
\mathbf{x}
x 的每个类的条件概率”,优化目标是最大化
P
(
Y
∣
X
)
P(\mathbf{Y\vert X})
P(Y∣X),可以转换为最小化负对数似然:
−
log
P
(
Y
∣
X
)
=
∑
i
=
1
n
−
log
P
(
y
(
i
)
∣
x
(
i
)
)
=
∑
i
=
1
n
l
(
y
(
i
)
,
y
^
(
i
)
)
(6)
-\log P(\mathbf{Y\vert X})=\sum_{i=1}^n-\log P(\mathbf{y}^{(i)}\vert\mathbf{x}^{(i)})=\sum_{i=1}^nl(\mathbf{y}^{(i)},\hat{\mathbf{y}}^{(i)})\tag{6}
−logP(Y∣X)=i=1∑n−logP(y(i)∣x(i))=i=1∑nl(y(i),y^(i))(6)
l
(
y
(
i
)
,
y
^
(
i
)
)
=
−
∑
j
=
1
q
y
j
log
y
^
j
(7)
l(\mathbf{y}^{(i)},\hat{\mathbf{y}}^{(i)})=-\sum^q_{j=1}y_j\log{\hat{y}_j}\tag{7}
l(y(i),y^(i))=−j=1∑qyjlogy^j(7)
式(7)中的损失函数通常被称为交叉熵损失(cross-entropy loss),是分类问题最常用的损失之一。由于幂永远大于零,得到的概率一定大于零,理论上损失函数不能被进一步最小化。
8. [导数计算]将式(5)带入式(7),可以得到:
l
(
y
,
y
^
)
=
−
∑
j
=
1
q
y
j
log
exp
(
o
j
)
∑
k
exp
(
o
k
)
=
log
∑
k
=
1
q
exp
(
o
k
)
−
∑
j
=
1
q
y
j
o
j
(8)
l(\mathbf{y},\hat{\mathbf{y}})=-\sum^q_{j=1}y_j\log{\frac{\exp(o_j)}{{\sum}_k\exp(o_k)}}=\log\sum_{k=1}^q \exp(o_k)-\sum_{j=1}^qy_jo_j\tag{8}
l(y,y^)=−j=1∑qyjlog∑kexp(ok)exp(oj)=logk=1∑qexp(ok)−j=1∑qyjoj(8)
得到损失相对于任何未规范化的预测
o
j
o_j
oj 的导数:
∂
o
j
l
(
y
,
y
^
)
=
exp
(
o
j
)
∑
k
=
1
q
exp
(
o
k
)
−
y
j
=
softmax
(
o
)
j
−
y
j
(9)
\partial_{o_j}l(\mathbf{y},\hat{\mathbf{y}})=\frac{\exp(o_j)}{{\sum}^q_{k=1}\exp(o_k)}-y_j=\text{softmax}(\mathbf{o})_j-y_j\tag{9}
∂ojl(y,y^)=∑k=1qexp(ok)exp(oj)−yj=softmax(o)j−yj(9)
9. [熵的计算], 核心思想是量化数据中的信息内容,这个数值在信息论中称为分布
P
P
P 的熵(entropy),计算方法为
H
[
P
]
=
∑
j
−
P
(
j
)
log
P
(
j
)
H[P]=\sum_j-P(j)\log P(j)
H[P]=∑j−P(j)logP(j),纳特、比特…
[压缩与预测] 想象一个需要压缩的数据流,如果很容易预测下一个数据,则很容易被压缩,而当我们不能完全预测每一个时间,就会感到“惊异”,香农决定用信息量
log
1
P
(
j
)
=
−
log
P
(
j
)
\log\frac{1}{P(j)}=-\log P(j)
logP(j)1=−logP(j) 来量化这种惊异,我们赋予一个事件较低的概率,我们的惊异越大,包含的信息量也就越大,而上面的熵则是当分配的概率真正匹配数据生成过程的信息量的期望。
[熵与交叉熵的理解] 把熵
H
(
P
)
H(P)
H(P) 想象为“知道真实概率的人所经历的惊异程度”,交叉熵
H
(
P
,
Q
)
H(P,Q)
H(P,Q) 则是“主观概率为
Q
Q
Q 的观察者在看到根据概率
P
P
P 生成的数据时的预期惊异”,
P
=
Q
P=Q
P=Q 时交叉熵达到最低
[交叉熵分类目标] 可以从两个方面考虑交叉熵分类目标:① 最大化观测数据的似然;② 最小化传达标签所需的惊异。
10. [模型预测评估] 使用预测概率最高的类别作为输出类别,如果预测与实际类别一致,则预测是正确的。使用精度(正确预测数与预测总数之间的比率)来评估模型的性能。
3.2.2 softmax回归的从零开始实现
3.2.3 softmax回归的简洁实现
3.3 图像分类数据集
MNIST (LeCun et al., 1998) 是图像分类中广泛使用的数据集之一,但是作为基准数据集过于简单,Fashion-MNIST (Xiao et al., 2017)数据集类似但更加复杂,是一个服装分类数据集,它由10个类别的图像组成,每个类别由训练集6000张图像和测试集1000张图像组成。
""" 导入所需库 """
%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
d2l.use_svg_display()
""" 读取数据集 """
# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式,
# 并除以255使得所有像素的数值均在0~1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
root="../data", train=False, transform=trans, download=True)
len(mnist_train), len(mnist_test) # (60000, 10000)
mnist_train[0][0].shape # torch.Size([1, 28, 28])
""" 在数字标签索引及其文本名称之间转换 """
def get_fashion_mnist_labels(labels): #@save
"""返回Fashion-MNIST数据集的文本标签"""
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
return [text_labels[int(i)] for i in labels]
""" 可视化样本图像 """
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5): #@save
"""绘制图像列表"""
figsize = (num_cols * scale, num_rows * scale)
_, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
axes = axes.flatten()
for i, (ax, img) in enumerate(zip(axes, imgs)):
if torch.is_tensor(img):
# 图片张量
ax.imshow(img.numpy())
else:
# PIL图片
ax.imshow(img)
ax.axes.get_xaxis().set_visible(False)
ax.axes.get_yaxis().set_visible(False)
if titles:
ax.set_title(titles[i])
return axes
""" 展示图像 """
X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y));
为了使训练集、测试集的读取更容易,一般使用Pytorch内置的数据迭代器而非从零开始创建。数据迭代器在每次迭代中读取一小批量数据(大小为batch_size),并且可以随机打乱样本,从而保证无偏。
batch_size = 256
def get_dataloader_workers(): #@save
"""使用4个进程来读取数据"""
return 4
train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers())
""" 统计时间 """
timer = d2l.Timer()
for X, y in train_iter:
continue
f'{timer.stop():.2f} sec'
整合组件
def load_data_fashion_mnist(batch_size, resize=None): #@save
"""下载Fashion-MNIST数据集,然后将其加载到内存中"""
trans = [transforms.ToTensor()]
if resize:
trans.insert(0, transforms.Resize(resize))
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(
root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
root="../data", train=False, transform=trans, download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers()),
data.DataLoader(mnist_test, batch_size, shuffle=False,
num_workers=get_dataloader_workers()))
train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
for X, y in train_iter:
print(X.shape, X.dtype, y.shape, y.dtype) # torch.Size([32, 1, 64, 64]) torch.float32 torch.Size([32]) torch.int64
break