1. 简介

  统计学中最核心的概念之一是：标准差及其与其他统计量（如方差和均值）之间的关系，本文将对标准差这一概念提供直观的视觉解释，在文章的最后我们将会介绍协方差的概念。

2. 概念介绍

均值

  均值： 均值就是将所有的数据相加求平均，求得一个样本数据的中间值。

• 定义： 给定一个包含n个样本的集合 X={X1, …Xn}，均值就是这个集合中所有元素和的平均值。
  

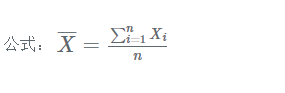
方差

  方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量，换句话说如果想知道一组数据之间的分散程度的话就可以使用“方差”来表示了。

• 定义：在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。
  

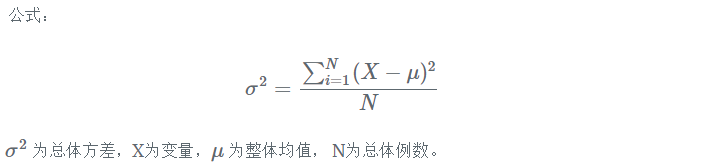
标准差

  又叫均方差，是离均差平方的算术平均数的平方根，用σ表示。标准差是”方差”的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。

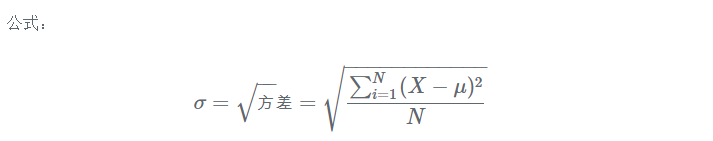
3. 概念描述

  举例而言，假设你收集了一些学生分数（出于简洁性考虑，我们假设这些分数是总体）。
  
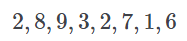
  我们首先在简单的散点图中绘制这些数字：
  
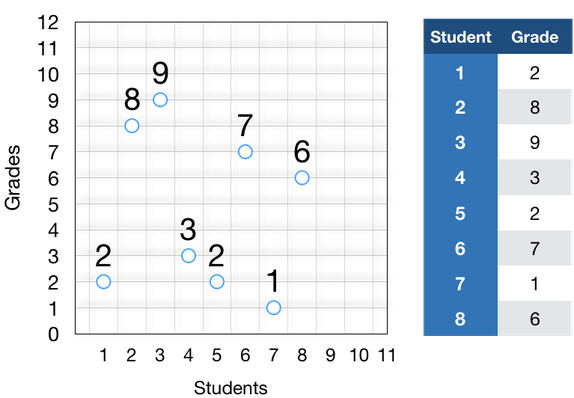
  绘制完成后，计算差异的第一步是找出这些数字的中心，即平均值，这也就是前面所说的均值的概念。
  
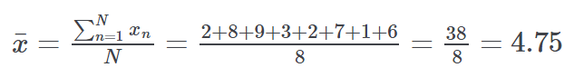
  视觉上，我们可以绘制一条线来表示平均分数。
  
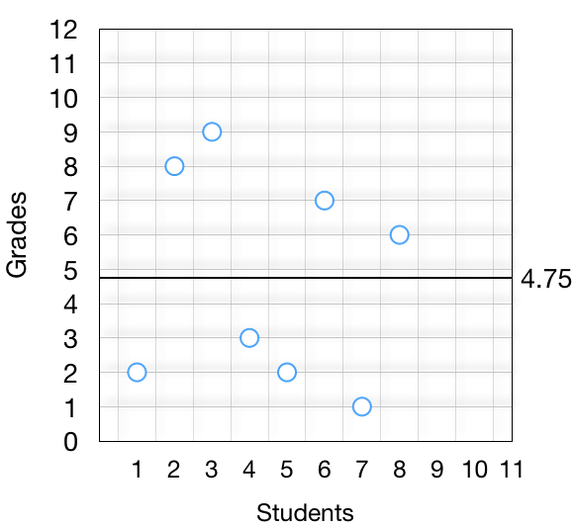
  接下来我们要计算每个点和平均值之间的距离，并对得到的数值求平方。记住，我们的目标是计算数字之间的差异，以及数字与平均值之间的差异。我们可以用数学或视图的方式完成该操作：
  
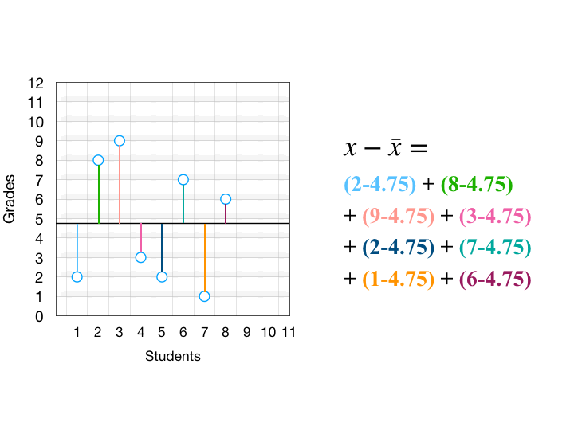
  从上图中我们可以看到，「求平方」只不过是画了一个方框而已。这里有两点需要注意：我们无法计算所有差异的总和。因为一些差异是正值，一些是负值，求和会使正负抵消得到 0。为此，我们对差异取平方（稍后我会解释为什么取平方而不是其他运算，如取绝对值）。现在，我们来计算差异平方的总和（即平方和）：
  
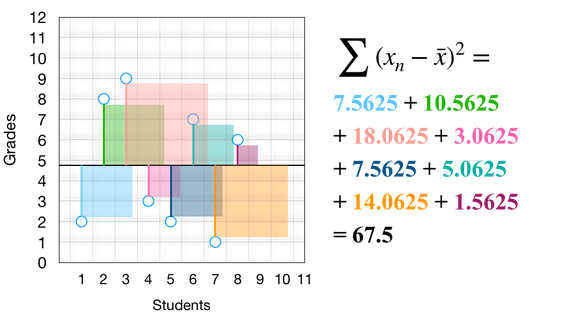
  通过计算平方和，我们高效计算出这些分数的总变异（即差异）。理解变异（variability）与差异（difference）之间的关系是理解多个统计估计和推断检验的关键。上图中平方和 67.5 表示，如果我们将所有方框堆在一个巨大的正方形中，则大正方形的面积等于 67.5 points^2，points 指分数的单位。任意测量集的总变异都是正方形的面积。

  现在我们得到了总变异（即大正方形的面积），但我们真正想要的是平均变异（mean variability）。要想求得平均变异，我们只需要用总面积除以方框的数量：
  
  
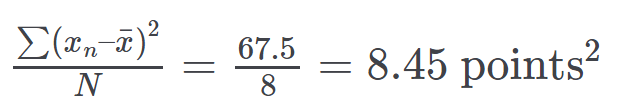
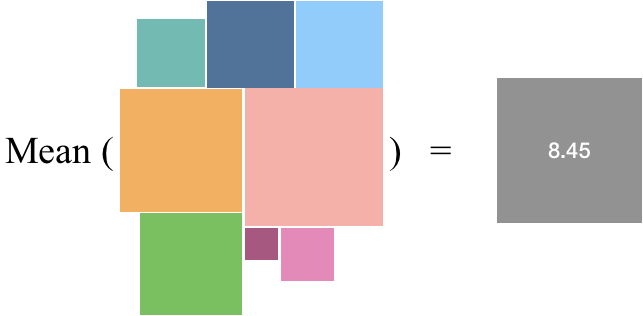
  出于实用目的考虑，你或许想除以 N−1，而不是 N，这样你就可以尝试基于一个样本而不是总体来估计平均变异。但是，这里假设我们已经具备总体。重点在于，你想计算所有小方框的均方值。这就是方差，即平均变异，或者差异平方的平均值。

  我们为什么不用方差来表示分数的差异呢？唯一的问题是，我们无法对比方差和原始分数，因为方差是「平方」值，即它是面积而非长度。其单位是 points^2，与原始分数的单位 points 不同。那么如何甩掉平方呢？开平方根啊！
  
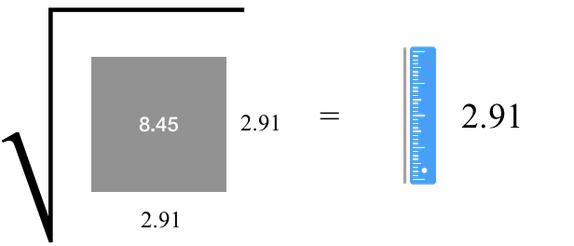
  最后，我们终于得到了标准差：变异的平方根，即 2.91points。这就是标准差的核心理念。本文对标准差概念的基础直观解释可以帮助大家更容易地理解，为什么在处理 z 分数（z-score）、正态分布、标准误差和方差分析时要使用标准差的单位。

绝对值的问题

  你可能会疑惑，为什么对差异求平方而不是取绝对值呢。没有什么能够真正阻止你使用差异的平均绝对值。平均绝对值给所有差异提供的是相同的权重，而差异平方为距离平均值较远的数字提供更多权重。这或许是你想要的。但是，大部分数学理论利用差异平方（其原因不在本文讨论范围内，如可微分）。不过，我会用一个容易理解的反例来回答这个问题。假设有两个均值相同的分数集合：x_1 和 x_2：
  
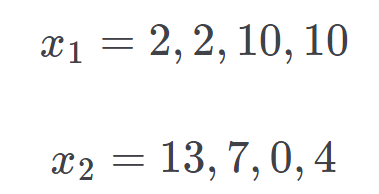
  从这些数字中，你可以轻松观察到 x_1 的变异和数值分散性比 x_2 低。我们来计算两个集合差异的平均绝对值（二者的平均值都为 6）：
  
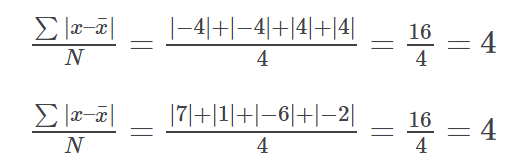
  哦，结果并不好！两个集合的变异值相同，尽管我们能够看到 x_1 的数字差异要比 x_2 低。现在，我们使用差异平方计算，得到：
  
  在差异平方的作用下，我们得到了想要的结果：当数字越分散时，标准差越大。

协方差

  前面的方差、标准差描述的是一维数据集合的离散程度，但世界上的现象普遍是多维度数据描述的。那么很自然就会想知道现象和数据的相关程度，以及各维度数据间的相关程度。比如，一个产品卖的好不好可能有很多因素构成，比如产品质量、价格等。那么是否质量和价格之间有相关性呢？这个问题就可以用协方差来解决。协方差的计算公式被定义为：
  
  期望值分别为 E(X) 和 E(Y) 的两个变量X和Y的协方差为：

Cov(X,Y)=E[(X−E(X))(Y−E(Y))]
		=E(XY)−2E(X)E(Y)+E(X)E(Y)
		=E(XY)−E(X)E(Y)

  协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。
如果X 与Y 是统计独立的，那么二者之间的协方差就是0，则：

E(XY)=E(X)E(Y)

参考资料：
《https://www.jiqizhixin.com/articles/2020-01-25-2》