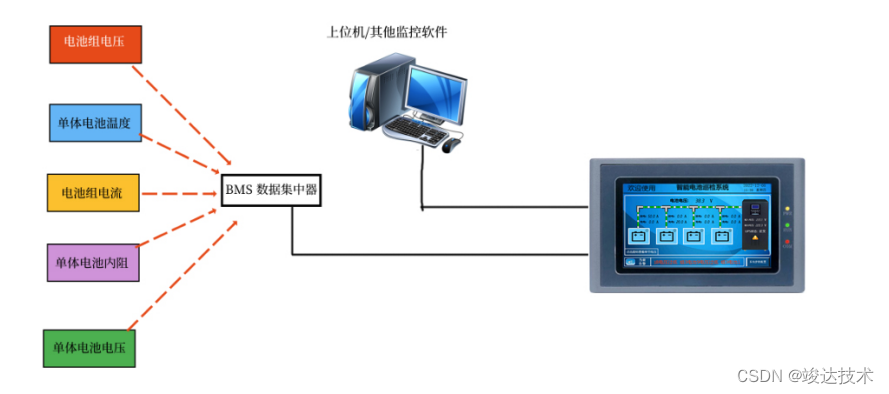
我们先求到区间[1..b]之间的所有约数之和
于是结果就等于
[1..b]之间的所有约数之和减去[1..a-1]之间的约数之和
很明显这两个问题是同性质的问题,只是右端点不同罢了.
明显对于1到N之间的数字,其约数范围也为1到N这个范围内。
于是我们可以枚举约数L,当然这个枚举不可能是for循环枚举,而是如上题一样“跳跃式的”
于是N/L就代表1到N之间有多少个数字是L的倍数,L也必为它们的约数。
例如当L=7时,N=20时
N/20=2,说明1到20以内有两个数字是7的倍数,易知为7,14,也就是说在算7和14的约数之和时,必然要将7统计进去。
然后这个算法高明的地方在于
当L=8,9,10时,N/L=2
于是这一段的L=7,R=10
于是这一段的约数之和为2*7+2*8+2*9+2*10=2*(7+8+9+10)=2*(7+10)*(10-7+1)/2
当统计完这一段后,设L=R+1=10+1=11
会发现11做为约数,只会出现1次
同时还会发现12,13,14.........20整个这一段的约数,都只会出现1次
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m;
ll f(ll x)
{
ll l = 1,r = 0,k = 0,ans = 0,m = 0;
while(l <= x)
{
r = x / (x / l);
k = x / l;
ans += k * (l + r) * (r - l + 1) / 2;
l = r + 1;
}
return ans;
}
signed main()
{
cin>>n>>m;
cout<<f(m) - f(n - 1);
return 0;
}