引言

在上一篇文章中，我们提到判断一个算法的好坏的标准是时间复杂度与空间复杂度。

时间复杂度的作用是衡量一个算法运行的快慢；而空间复杂度是衡量一个算法运行所需的额外的空间。在上一篇文章中，我们已经了解了计算时间复杂度的方法，以及如何使用大O阶表示法来表示时间复杂度的大概值。
戳我转到时间复杂度详解哦

在本篇文章中将详细介绍关于空间复杂度的相关内容：

空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中所额外占用的空间大小的量度。

在时间复杂度中，我们以算法中基本语句执行的次数作为算法的时间复杂度；
而空间复杂度中，我们以变量被创建的个数作为算法的空间复杂度（不论是什么类型的变量，都算做一个空间复杂度）。

需要注意的是：由于函数运行时需要的栈空间在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定（参数等一些数据不必计算）。

我们在计算空间复杂度时，依旧采用大O阶表示法来确定其大概值。
转换大O阶表示的方式与时间复杂度相同：
1、用常数1表示算法中的所有加法常数；
2、在修改后的数学表达式中只保留最高项；
3、如果最高项存在且不是1，则去掉该最高项的系数。

但是，通常情况下，我们是不需要将精确的空间复杂度计算出来后再转换的。与时间复杂度相同，空间复杂度的大O阶表示法也分为例如对数级（log n）、正比例级（n）、次方级（n^2）、指数级（2^n）等：
在这里插入图片描述
但是对于空间复杂度而言，最常见的就是O(1)与O(n)，其他量级就不是很常见。

例题

接下来就通过几个栗子来理解空间复杂度：

test1

int* rotate(int* nums, int numsSize, int k)
{
	int* ret = (int*)calloc(numsSize, sizeof(int));
	int i = 0;
	for (i = numsSize-k; i < numsSize ; i++)
	{
		*ret++ = nums[i];
	}
	for (i = 0; i < numsSize - k; i++)
	{
		*ret++ = nums[i];
	}
	return ret-numsSize;
}

在这段算法中，我们实现了将数组的后k个元素移动到数组的前面。

在计算这个算法的空间复杂度时，数组nums、整型numsSize与k均为参数，所以不计算空间复杂度。在实现元素的移动时，我们动态开辟了一块空间，这块动态空间由numsSize个整型，所以这个算法的空间复杂度就是O(n)。

不难发现，在算法中还创建了一个整型变量i，但是，这个常数就省略不计了。

test2（冒泡排序）

void BubbleSort(int* a, int n)
{
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

这段算法是经典的冒泡排序。

在段算法中，额外申请了三个整型变量end、exchange、i 。空间复杂度是常数，大O表示法中常数忽略后表示为O(1)。

test3（求阶乘）

long long Fac(size_t N)
{
	if (N == 0)
		return 1;
	return Fac(N - 1) * N;
}

此算法可以实现求N的阶乘。

在这个算法中，我们通过函数递归的方式，每次递归将N-1作为参数，返回Fac(N - 1) 与 N的乘积。
参数为0时，递归终止，开始返回值。

这里需要注意的是，函数在栈中开辟函数栈帧时是依次开辟的。当函数调用它本身时，会在栈中再开辟一块空间作为新的函数的栈帧。在每一块栈帧中，并没有创建额外的变量，所以我们可以认为每一块栈帧的空间复杂度是常数个。所以，有多少次递归，就会有多少个函数的栈帧。
我们可以画图来表示在这个算法中栈帧的开辟：
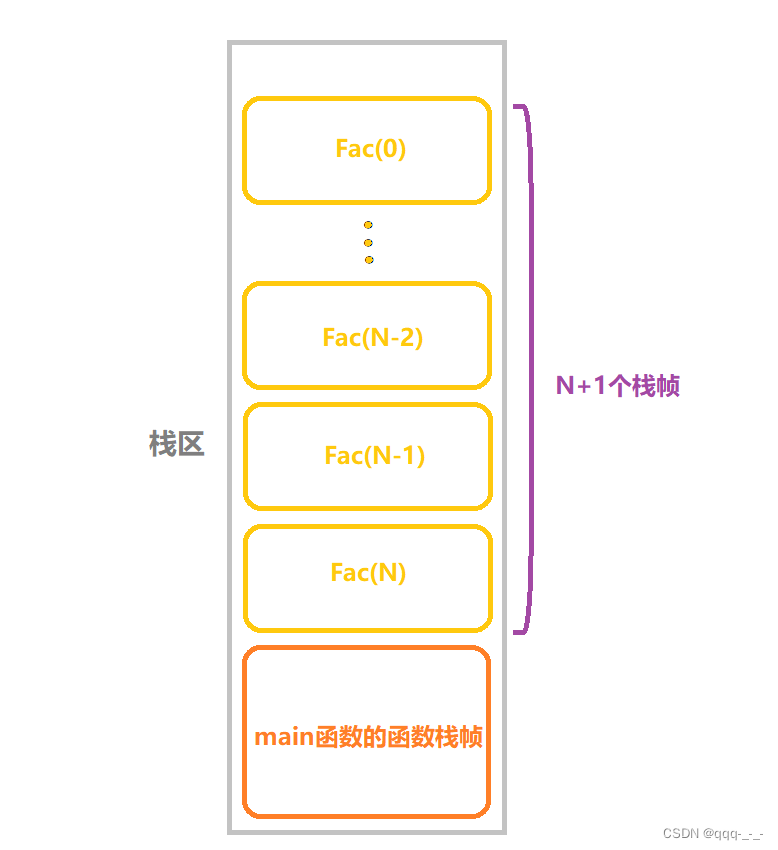
在这里插入图片描述
从参数为N递归到参数为0，共递归了N+1次。省略常数1，该算法的空间复杂度就是O(n)。

test4（斐波那契数列）

long long Fib(size_t N)
{
	if (N < 3)
		return 1;
	return Fib(N - 1) + Fib(N - 2);
}

此算法通过递归实现计算第n个斐波那契数。

在上一篇文章中，我们介绍了这个算法的时间复杂度的计算，结果是O(2^n)。通过计算时间复杂度，我们了解了这个算法的递归规律：
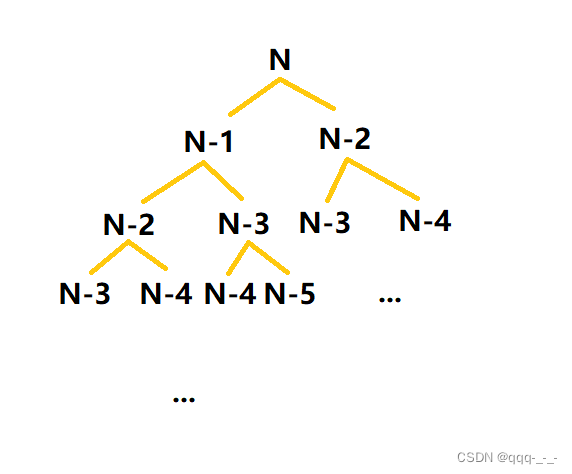
在这里插入图片描述
根据上一个例题，我们知道，在这种没有新建变量的递归中，每次递归的空间复杂度都可以看作常数。大概是递归了2^n次，那空间复杂度也是O(2^n)吗？

其实并不是，其实这个算法的空间复杂度是O(n)。

函数调用时会为函数开辟一块栈帧，当函数调用结束后，这块空间就会被还给操作系统。这块空间是可以重复利用的。比如在调用某函数结束后，再次调用相同的函数时，所用的空间与上次调用完的空间是相同的，这里举一个小栗子：

void Fun1()
{
	int i = 10;
	printf("%p\n", &i);
}
void Fun2()
{
	int j = 10;
	printf("%p\n", &j);
}
int main()
{
	Fun1();
	Fun2();
	return 0;
}

在这里插入图片描述
这段代码中，main函数调用了两个相同的函数Fun1与Fun2。在这两个函数中都创建了一个整型的变量。我们打印这两个变量的地址，发现它们是相等的。这就说明这两个函数所使用的是同一块空间。

再回到斐波那契数列。这个算法的递归并不是我们想象的一次递归同时开辟两个函数栈帧，而是先在一条线上递归到终止后返回一个值，释放此次递归的空间，再回到上一级的递归，然后再到终止后返回一个值，再释放此次的空间，然后再回到上一级递归，释放空间。最终，将所有的返回值汇到最初的函数中，得到最终的结果：
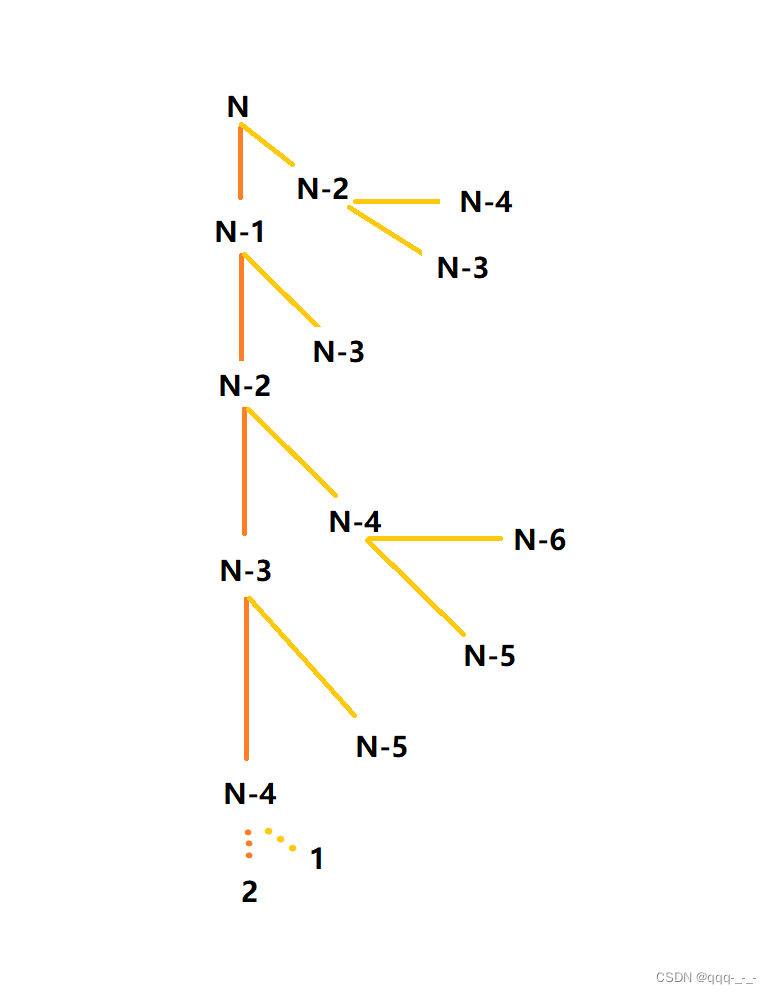
在这里插入图片描述
这张图示应该可以比较清楚地描述该算法的递归：

首先顺着第一条线递归，直到小于3时终止。到此，函数一共递归N-1次，空间复杂度为O(n)。返回1后，为Fib(2)开辟的栈帧被释放；下一步调用Fib(1)，并为其开辟空间，这时开辟的空间与刚才Fib(2)的空间是同一块该函数的参数也小于3，递归终止，返回1，为Fib(1)开辟的栈帧被释放。此时，Fib(N-4)的返回值就可以被计算出来，即Fib(2)与Fib(1)的和（假设N-4-1的值为2），返回后，为Fib(N-4)开辟的空间也被释放；接下来为Fib(N-5)开辟栈帧，该空间与刚才释放的Fib(N-4)的函数栈帧是同一块空间…

依次类推，其实该算法开辟的空间就只有最开始第一条线递归时所开辟的空间，后面的递归开辟空间时使用的都是之前释放的空间。所以，该算法的空间复杂度就是O(n)。

通过这个斐波那契数列的递归算法，我们不难发现：
时间是一去不复返的，在运行基本语句时，势必要消耗时间；
而空间是可以重复利用的，我们在使用完一块空间后，该空间被释放后是可以再次利用的。
所以在许多的算法中，会使用空间换时间的思想，尽量先保证时间复杂度的减少。