一、选择题(30分)
1.设某无向图有n个顶点,则该无向图的邻接表中有( B )个表头结点。
(A) 2n (B) n ( C) n/2 (D) n(n-1)
n
表头结点数=顶点数
2.设无向图G中有n个顶点,则该无向图的最小生成树上有( B )条边。
(A) n (B) n-1 ( C) 2n (D) 2n-1
一个顶点和其他的n-1个顶点相连,共n-1条边
3.设一组初始记录关键字序列为(60,80,55,40,42,85),则以第一个关键字60为基准而得到的一趟快速排序结果是( C )。
(A) 40,42,60,55,80,85 (B) 42,40,55,60,85,80
( C) 42,40,55,60,80,85 (D) 42,40,60,85,55,80
60 80 55 40 42 85
42 60 55 40 80 85
42 40 60 55 80 85
42 40 55 60 80 85
4.( B )二叉排序树可以得到一个从小到大的有序序列。
(A) 先序遍历 (B) 中序遍历 © 后序遍历 (D) 层次遍历
左中右
5.设按照从上到下、从左到右的顺序从1开始对完全二叉树进行顺序编号,则编号为i结点的左孩子结点的编号为( B )。
(A) 2i+1 (B) 2i © i/2 (D) 2i-1
6.程序段s=i=0;do {i=i+1; s=s+i;}while(i<=n);的时间复杂度为( A )。
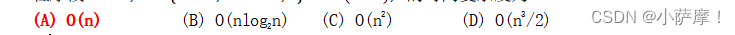
7.设带有头结点的单向循环链表的头指针变量为head,则其判空条件是( C )。
(A) head = =0 (B) head->next= =0
© head->next==head (D) head!=0
单向循环链表为空 那么头结点的下一个结点指向头结点本身。
8.设某棵二叉树的高度为10,则该二叉树上叶子结点最多有( C)。
(A) 20 (B) 256 ( C ) 512 (D) 1024
二叉树的结点个数最多有2^(h-1)
9.设一组初始记录关键字序列为(13,18,24,35,47,50,62,83,90,115,134),则利用二分法查找关键字90需要比较的关键字个数为( B)。
(A) 1 (B) 2 © 3 (D) 4
10.设指针变量top指向当前链式栈的栈顶,则删除栈顶元素的操作序列为( D )。
(A) top=top+1; (B) top=top-1;
© top->next=top; (D) top=top->next;
直接将top指针指向top的下一个元素。
二、判断题(20分)
1.不论是入队列操作还是入栈操作,在顺序存储结构上都需要考虑“溢出”情况。 ()
对
2.当向二叉排序树中插入一个结点,则该结点一定成为叶子结点。 ()
对
3.设某堆中有n个结点,则在该堆中插入一个新结点的时间复杂度为O(log2n)。 ( )
对
4,完全二叉树中的叶子结点只可能在最后两层中出现。 ()
对
5.哈夫曼树中没有度数为1的结点。 ( )
对。
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
6,对连通图进行深度优先遍历可以访问到该图中的所有顶点。 ()
对
连通图可以 非连通图不可以
7.先序遍历一棵二叉排序树得到的结点序列不一定是有序的序列。 ()
对 中序遍历才是
8.由树转化成二叉树,该二叉树的右子树不一定为空。 ( )
错 右子树一定为空 因为树根结点没有右兄弟
9.线性表中的所有元素都有一个前驱元素和后继元素。()
除了开头和结尾
错
10.带权无向图的最小生成树是唯一的。 ( )
错 最小生成树不一定是唯一的
三、填空题(30分)
1.设指针变量p指向双向链表中的结点A,指针变量s指向被插入的结点X,则在结点A的后面插入结点X的操作序列为______;s->right=p->right;______=s; p->right->left=s; (设结点中的两个指针域分别为left和right)。
s->left=p
p->right
2.设完全有向图中有n个顶点,则该完全有向图中共有_____条有向条;设完全无向图中有n个顶点,则该完全无向图中共有_____条无向边。
n(n-1)
n(n-1)/2
3.设关键字序列为(K,K2,…,Kn),则用筛选法建初始堆必须从第___个元素开始进行筛选。
“…我们称这个自堆至叶子的调整过程为筛选。从一个无序序列建堆过程就是一个反复筛选的过程。若将此序列看成是一个完全二叉树,则最后一个非终端结点是第[n/2]个元素,由此筛选只需从第[n/2]个元素开始” 出自严蔚敏《数据结构》280页。
4.解决散列表冲突的两种方法是__________
和______。
开放定址法
链地址法
5.设一棵三叉树中有50个度数为0的结点,21个度数为2的结点,则该二叉树中度数为3的结点数有___个。
由2叉树的性质引申出,对于任何一颗树T,如果其终端结点树为n0 度为的结点数为ni,则n0=1+n2+2n3+…+(i-1)ni.
n0=1+n2+2n3
代入 N0=50,N2=21
得 N3=14
6.高度为h的完全二叉树中最少有_____个结点,最多有_____个结点。
2^(h-1)
2 ^h -1
7.设有一组初始关键字序列为(24,35,12,27,18,26),则第3趟直接插入排序结束后的结果的是_____
8.设有一组初始关键字序列为(24,35,12,27,18,26),则第3趟简单选择排序结束后的结果的是_____
选择排序基本思想:
在长度为N的无序数组中,第一次遍历n-1个数,找到最小的数值与第一个元素交换;
第二次遍历n-2个数,找到最小的数值与第二个元素交换;
。。。
第n-1次遍历,找到最小的数值与第n-1个元素交换,排序完成。
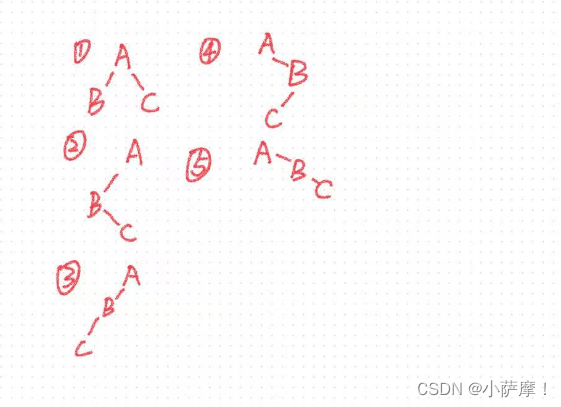
9.设一棵二叉树的前序序列为ABC,则有_____
种不同的二叉树可以得到这种序列。
5
10、
i<j&&r[[i].key<x.key
r[i]=x
四、算法设计题(20分)
1.设计在链式结构上实现简单选择排序算法。
排序算法的简单介绍:从序列的第一个数开始到最后一个数,找当前序列中最小的数与当前位置的数进行交换。
void simpleselectsorlklist(lklist *&head)
{
lklist *p,*q,*s;
int min,t;
if(head==0 ||head->next==0) return;
for(q=head; q!=0;q=q->next)
{
min=q->data;
s=q;
for(p=q->next; p!=0;p=p->next)
if(min>p->data){min=p->data; s=p;}
if(s!=q){
t=s->data;
s->data=q->data;
q->data=t;
}
}
}
2.设计在顺序存储结构上实现求子串算法。
void substring(char s[ ], long start, long count, char t[ ])
{
long i,j,length=strlen(s);
if (start<1 || start>length) printf("The copy position is wrong");
else if (start+count-1>length) printf("Too characters to be copied");
else { for(i=start-1,j=0; i<start+count-1;i++,j++) t[j]=s[i]; t[j]= '\0';}
}
3.设计求结点在二叉排序树中层次的算法。
int lev = 0;
typedef struct node {
int key;
struct node* lchild, * rchild;
}bitree;
void level(bitree* bt, int x)
{
if (bt != 0)
{
lev++;
if (bt->key == x) return lev;
else if (bt->key > x)
level(bt->lchild, x);
else level(bt->rchild, x);
}
}