问题
卷积神经网络是一类包含卷积计算且具有深度结构的前馈神经网络,是深度学习。卷积神经网络具有表征学习能力,能够按其阶层结构对输入信息进行平移不变分类,因此也被称为“平移不变人工神经网络。
全连接神经网络是具有多层感知器的的网络,也就是多层神经元的网络。层与层之间需要包括一个非线性激活函数,需要有一个对输入和输出都隐藏的层,还需要保持高度的连通性,由网络的突触权重决定。那两者的区别是什么呢?
方法
卷积神经网络也是通过一层一层的节点组织起来的。和全连接神经网络一样,卷积神经网络中的每一个节点就是一个神经元。在全连接神经网络中,每相邻两层之间的节点都有边相连,于是会将每一层的全连接层中的节点组织成一列,这样方便显示连接结构。而对于卷积神经网络,相邻两层之间只有部分节点相连,为了展示每一层神经元的维度,一般会将每一层卷积层的节点组织成一个三维矩阵。
除了结构相似,卷积神经网络的输入输出以及训练的流程和全连接神经网络也基本一致,以图像分类为列,卷积神经网络的输入层就是图像的原始图像,而输出层中的每一个节点代表了不同类别的可信度。这和全连接神经网络的输入输出是一致的。类似的,全连接神经网络的损失函数以及参数的优化过程也都适用于卷积神经网络。因此,全连接神经网络和卷积神经网络的唯一区别就是神经网络相邻两层的连接方式。
但是全神经网络无法很好地处理好图像数据,然而卷积神经网络却很好地客服了这个缺点,使用全连接神经网络处理图像的最大问题就是:全连接层的参数太多,对于MNIST数据,每一张图片的大小是28*28*1,其中28*28代表的是图片的大小,*1表示图像是黑白的,有一个色彩通道。假设第一层隐藏层的节点数为500个,那么一个全连接层的神经网络有28*28*500+500=392500个参数,而且有的图片会更大或者是彩色的图片,这时候参数将会更多。参数增多除了导致计算速度减慢,还很容易导致过拟合的问题。所以需要一个合理的神经网络结构来有效的减少神经网络中参数的个数。卷积神经网络就可以更好的达到这个目的。
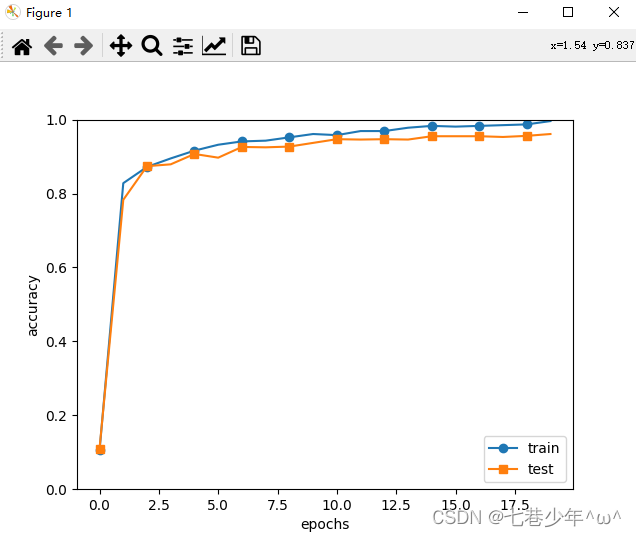
| from keras import layers from keras import models from keras.datasets import mnist from keras.utils import to_categorical (train_images, train_labels), (test_images, test_labels) = mnist.load_data('D:/Python36/Coding/PycharmProjects/ttt/mnist.npz') train_images = train_images.reshape(60000, 28*28) train_images = train_images.astype('float32') / 255 test_images = test_images.reshape(10000, 28*28) test_images = test_images.astype('float32') / 255 train_labels = to_categorical(train_labels) test_labels = to_categorical(test_labels) model = models.Sequential() model.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,))) model.add(layers.Dense(10, activation='softmax')) model.compile(optimizer='rmsprop',loss='categorical_crossentropy',metrics=['accuracy']) history=model.fit(train_images, train_labels, epochs=10, batch_size=128) test_loss, test_acc = model.evaluate(test_images, test_labels) print(test_acc,test_acc) #0.9786 0.9786 print("history_dict%s =" %history.history) #history_dict = {'loss': [0.25715254720052083, 0.1041663886765639, 0.06873120647072792, 0.049757948418458306, 0.037821156319851675, 0.02870141142855088, 0.02186925242592891, 0.01737390520994862, 0.01316443470219771, 0.010196967865650853], # 'acc': [0.9253666666984558, 0.9694833333333334, 0.9794666666348775, 0.9850166666984558, 0.9886666666666667, 0.9917666666666667, 0.9935499999682108, 0.9949499999682109, 0.9960999999682109, 0.9972833333333333]} = acc1 = history.history['acc'] loss1 = history.history['loss'] print(model.summary()) (train_images, train_labels), (test_images, test_labels) = mnist.load_data('D:/Python36/Coding/PycharmProjects/ttt/mnist.npz') train_images = train_images.reshape((60000, 28, 28, 1)) train_images = train_images.astype('float32') / 255 test_images = test_images.reshape((10000, 28, 28, 1)) test_images = test_images.astype('float32') / 255 train_labels = to_categorical(train_labels) test_labels = to_categorical(test_labels) model = models.Sequential() model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1))) model.add(layers.MaxPooling2D((2, 2))) model.add(layers.Conv2D(64, (3, 3), activation='relu')) model.add(layers.MaxPooling2D((2, 2))) model.add(layers.Conv2D(64, (3, 3), activation='relu')) model.add(layers.Flatten()) model.add(layers.Dense(64, activation='relu')) model.add(layers.Dense(10, activation='softmax')) model.compile(optimizer='rmsprop',loss='categorical_crossentropy',metrics=['accuracy']) history = model.fit(train_images, train_labels, epochs=10, batch_size=64) test_loss, test_acc = model.evaluate(test_images, test_labels) ##0.9919 0.9919 print("history_dict =%s" %history.history) #history_dict = {'loss': [0.1729982195024689, 0.04632370648694535, 0.031306330454613396, 0.02327785180026355, 0.01820601755216679, 0.01537780981725761, 0.011968255878429288, 0.010757189085084126, 0.008755202058390447, 0.007045005079609898], # 'acc': [0.9456333333333333, 0.9859, 0.9903333333333333, 0.9929333333333333, 0.99435, 0.9953333333333333, 0.9962333333333333, 0.9966, 0.99735, 0.9979333333333333]} acc2 = history.history['acc'] loss2 = history.history['loss'] print(model.summary()) import matplotlib.pyplot as plt fig=plt.figure() ax=fig.add_subplot(1,1,1) epochs = range(1, len(acc1) + 1) ax.plot(epochs, acc1, 'bo', label='dense Training acc',color='red') ax.plot(epochs, loss1, 'b', label='dense Training loss',color='red') ax.plot(epochs, acc2, 'bo', label='Conv2D Training acc',color='green') ax.plot(epochs, loss2, 'b', label='Conv2D Training loss',color='green') ax.legend(loc='best') ax.set_title('Training and validation accuracy by different model') ax.set_xlabel('Epochs') ax.set_ylabel('Accuracy') plt.show() 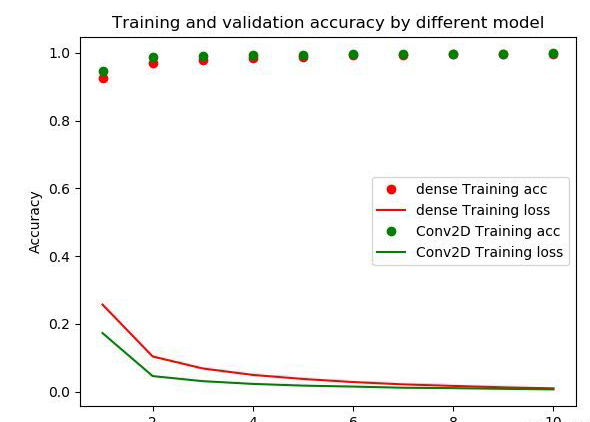 |
结语
全连接网络没有卷积层,只使用全连接层(以及非线性层)。
以关键是理解卷积层和全连接层的区别。
全连接层有三个特点:
关注全局信息(每个点都和前后层的所有点链接)
参数量巨大,计算耗时
输入维度需要匹配(因为是矩阵运算,维度不一致无法计算)
卷积层
这个卷积和信号系统中的卷积不太一样,其实就是一个简单的乘加运算,
局部链接:当前层的神经元只和下一层神经元的局部链接(并不是全连接层的全局链接)
权重共享:神经元的参数(如上图的3*3卷积核),在整个特征图上都是共享的,而不是每个滑动窗口都不同
也正是因为这两个特性,所以卷积层相比于全连接层有如下优点:
需要学习的参数更少,从而降低了过度拟合的可能性,因为该模型不如完全连接的网络复杂。
只需要考虑中的上下文/共享信息。这个未来在许多应用中非常重要,例如图像、视频、文本和语音处理/挖掘,因为相邻输入(例如像素、帧、单词等)通常携带相关信息。
但需要注意的是,无论是全连接层,还是卷积层,都是线性层,只能拟合线性函数,所以都需要通过ReLU等引入非线性,以增加模型的表达能力。比如ReLU函数接受一个输入x,并返回{0, x}的最大值。ReLU(x) = argmax(x, 0)。








![[Css]Grid属性简单陈列(适合开发时有基础的快速过一眼)](https://img-blog.csdnimg.cn/9d338deb4497486c91cdb94f242c0401.png)