首先注意数值求导和自动求导在使用的时候的不同之处。

实际上，正是自动求导这个地方使用了类模板，导致它不仅可以传入参数，还可以传入Jet类型的数据，从而实现了参数的雅可比矩阵的计算，完成自动求导。下面会详细分析。

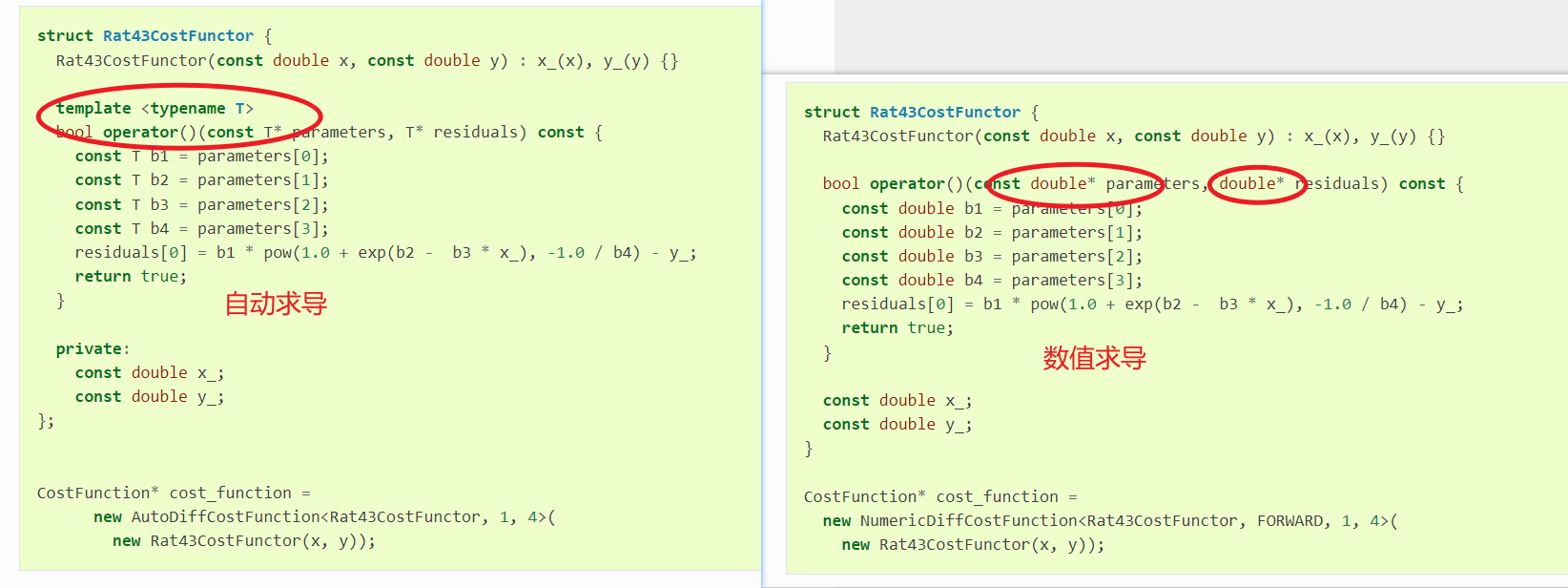
数学原理

考虑我们需要求取一个函数在一个点的导数，我们直接给自变量添加一个无穷小量，然后对函数进行展开，之后就会发现无穷小量的系数就是函数关于变量在该点的导数。

实现原理

Ceres里面的自动求导通过设计了一个Jet数据结构（这个东西在数学原理上称为Dual Number），Jet数据结构包含两个部分，类似于复数一样，一部分是一个实数成员变量(即函数值)，另一部分是一个固定大小的向量（即导数）。在求解器迭代过程中，Ceres Solver使用Jet类的对象来计算代价函数及其导数，并更新这些对象的值。

Ceres 实现的 Dual Number 的结构是 ceres::Jet，Jet 结构中的大量是 T a;，小量是 Eigen::Matrix v;（此处小量使用一个 Eigen::Vector 表达是基于多元函数对多个变量求导的考虑）。另外，因为Jet里面是包含了两个基本元素的，为了使得我们能够实现自动求导，我们需要对一些运算符进行重载，这里的一个基本思想就是“忽略高阶无穷小，仅保留一介无穷小”。下面是官网的一个实现方式：

有了上面这个Jet的基本定义之后，下面分析一下从观测量传入到实现自动求导这个过程。首先看我们在使用自动求导的时候是怎么调用AutoDiffCostFunction

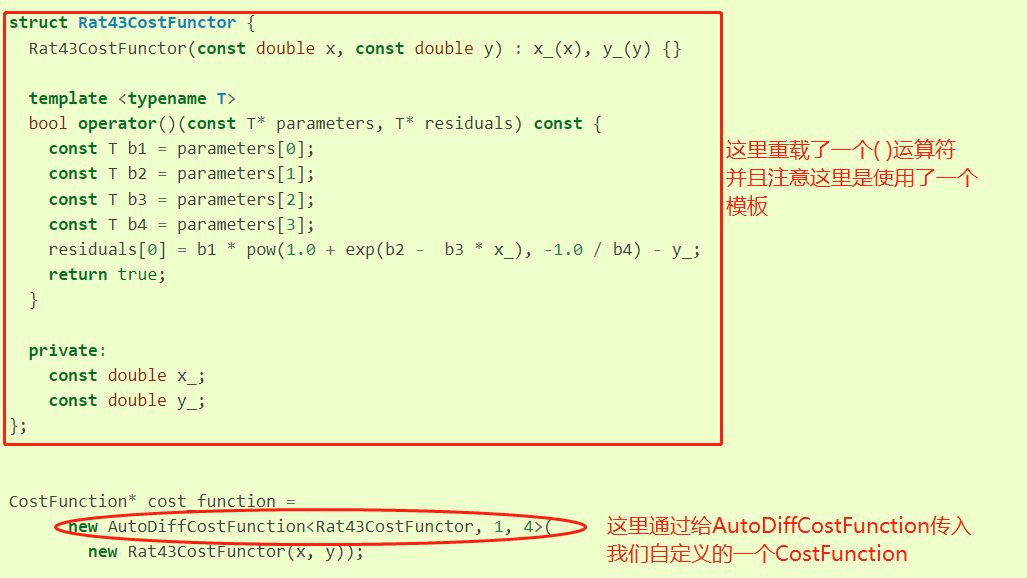
这里官网给了一个例子模拟了利用Jet实现对自定义CostFuntion导数计算的例子

总结

以上就是自动求导实现的原理。更本质和关键来说：实现这个自动求导的就是通过把残差的计算分解为Jet这种数据类型来进行计算！！！。经过一次残差计算就可以一方面获得残差Jet.a，另外一方面获得残差对变量在该work point的导数值Jet.v，接下来就是解析导的那一套。