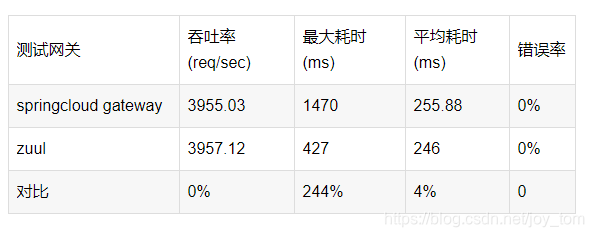
看见统计——第五章 统计推断：贝叶斯学派

引言

推理的频率学派认为，概率在本质上是与频率联系在一起的。这种解释实际上是很自然的。按照频率学派的说法，一枚公平的硬币出现人头的概率是1/2。简单地说，在同一个硬币的无限次独立抛掷中，有一半会出现头像。许多随机实验事实上是可以重复的，频率学派范式很容易适用于这种情况。

然而，给不可重复的事件分配概率通常是可取的。例如，当天气预报告诉你明天有90%的可能性下雨时，它是在为一次性事件分配概率，因为明天只会发生一次。更重要的是，在许多情况下，我们希望将概率分配给具有不确定性的非随机事件。银行可能有兴趣设计一个自动化系统，计算支票上的签名是否真实的概率。即使存在一个潜在的事实(签名是真的还是假的)，从银行的角度来看存在不确定性，因此使用概率是合理的。纯频率论对概率的解释不能很好的匹配这些用例中。

贝叶斯推理采取了一种主观的方法，并将概率视为代表信念（belief）的程度。因此，只要存在我们希望量化的不确定性，为非重复和非随机事件分配概率是完全有效的。贝叶斯概率是主观的这一事实并不意味着它们是任意的。使用贝叶斯概率的规则与使用频率主义概率的规则是相同的。贝叶斯主义者只是乐于将概率分配给比频率论者更大的一类事件。

而贝叶斯推理的基本精神被贝叶斯定理所囊括。

贝叶斯定理Bayes’ Theorem

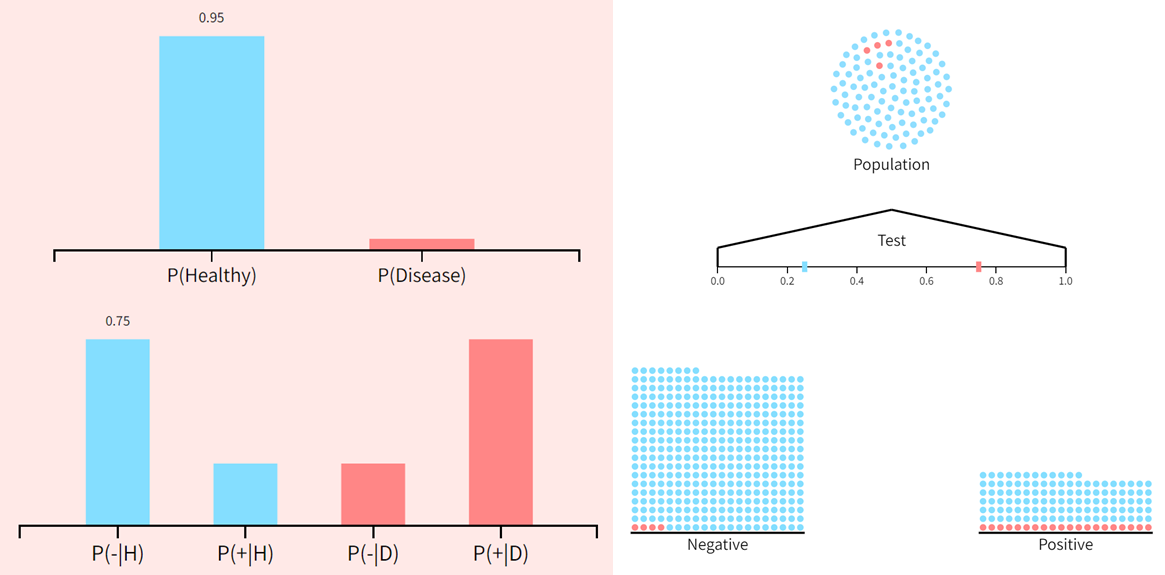
假设在一次常规体检中，医生通知你，你在一种罕见的疾病检测中呈阳性。这让你很苦恼，但作为一个优秀的统计学家，你也知道这些测试结果存在一些不确定性。可是不幸的是，这个测试相当准确——它对95%的疾病患者报告为阳性结果，而对95%的健康患者报告为阴性结果。

如果我们让 "+“和”-"分别表示阳性和阴性的测试结果，那么测试准确率就是条件概率
$$\begin{array}{rl}& P(+|疾病)=0.95\\ & P(-|健康)=0.95\end{array}$$
你感兴趣的是
$$P(疾病|+)$$
为了计算这最后一个量，我们对条件概率做一些变换。这可以通过贝叶斯定理来实现

📏 定理 ：贝叶斯定理(Bayes’ Theorem) 让 $Y_1,...,Y_k$是样本空间$\Omega$ 的一部分，$X$ 是任意事件，则有
$$P(Y_j|X)=\frac{P(X|Y_j)P(Y_j)}{{\sum }_{i=1}^{k}P(X|Y_i)P(Y_i)}$$
由于 "疾病 "和 "健康 "分割了结果的样本空间，我们有
$$P(疾病|+)=\frac{P(+|疾病)P(疾病)}{P(+|疾病)P(疾病)+P(+|健康)P(健康)}$$
重要的是，贝叶斯定理显示，为了计算在测试呈阳性的情况下你患有该疾病的条件概率，你需要知道在没有任何信息的情况下你患有该疾病的 "先验 "（prior）概率 $P(疾病)$。也就是说，你需要知道该疾病在你所属人群中的总体发病率。我们前面提到，这是一种罕见的疾病。事实上，只有千分之一的人受到影响，所以 $P(疾病)=0.001$，这又意味着 $P(健康)=0.999$。将这些数值插入上面的方程式中，可以得到
$$P(疾病|+)\approx 0.019$$
换句话说，尽管测试表面上很可靠，但你真正患有这种疾病的概率仍然低于2%。该疾病如此罕见的事实意味着大多数测试呈阳性的人都是健康的。请注意，该测试当然不是无用的；得到一个阳性结果会使你患这种疾病的概率增加大约20倍。但是将95%的测试准确率解释为患病的概率是不正确的。

贝叶斯过程The Bayesian procedure

上面的例子说明了做贝叶斯推理的一般过程。假设你对某个参数 $\theta$ 感兴趣

1. 将你对 $\theta$ 的初始信念以先验分布 $P(\theta )$ 的形式编码。

2. 通过实验、观察、查询等方式收集数据 $X$。

3. 使用贝叶斯定理对后验分布更新信念
   $$P(\theta |X)=\frac{P(X|\theta )P(\theta )}{P(X)}$$

4. 随着更多数据的出现，重复整个过程。

先验，似然，后验Prior, likelihood, posterior

先验Prior

先验分布是无条件分布 $P(\theta )$ 。先验分布的目的是在我们看到任何数据之前，捕捉我们对 $\theta$ 的预先存在的知识。在医学测试的例子中，我们用人口中的疾病发病率作为任何特定个体患有该疾病的先验概率。

似然Likelihood

在贝叶斯和频率主义统计学中，给定数据 $X$ 的参数 $\theta$ 的似然（Likelihood）是$P(X|\theta )$。似然函数在经典统计学中起着如此重要的作用，以至于它有了自己的字母：
$$L(\theta |X)=P(X|\theta )$$
这种表示法强调了这样一个事实，即对于某些固定数据 $X$ ，我们将似然视为 $\theta$ 的函数，等于给定参数 $\theta$ 后变量 $X$ 的概率。

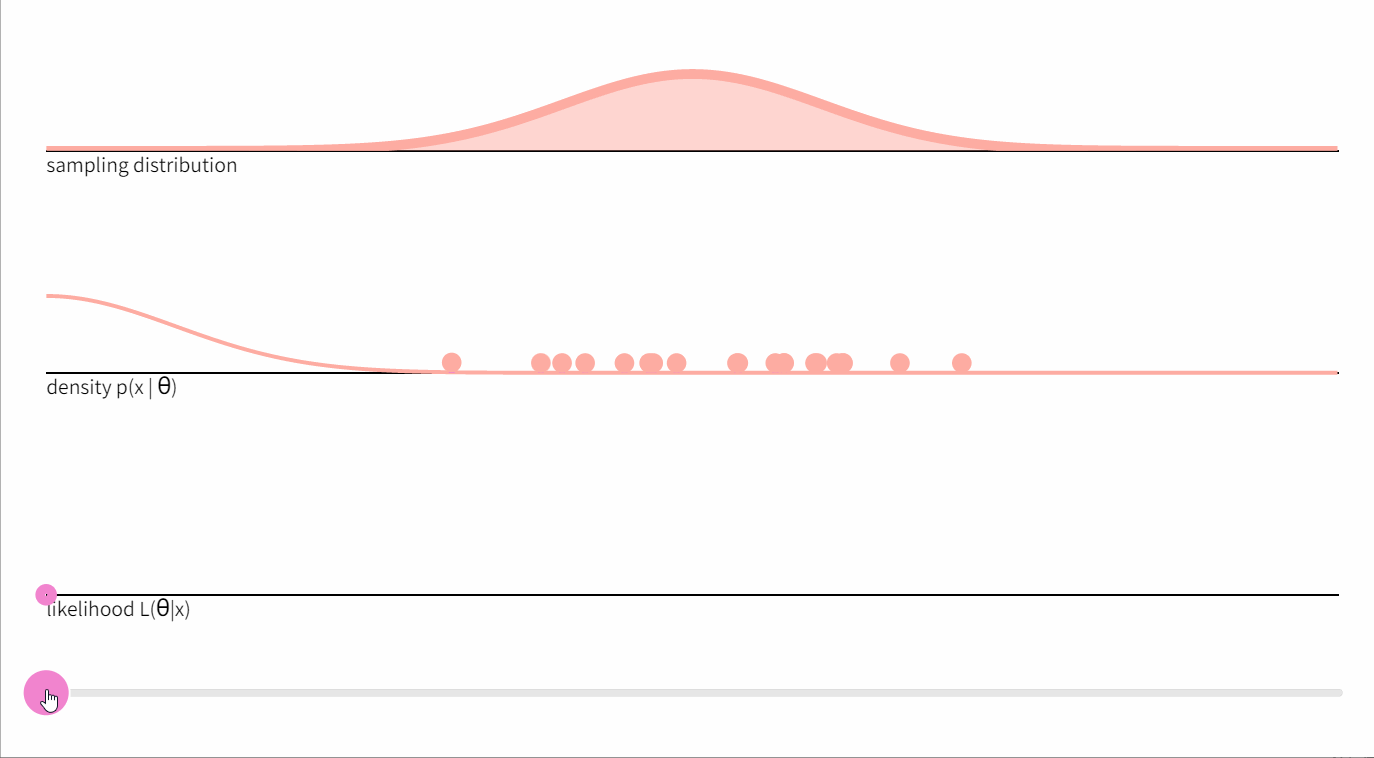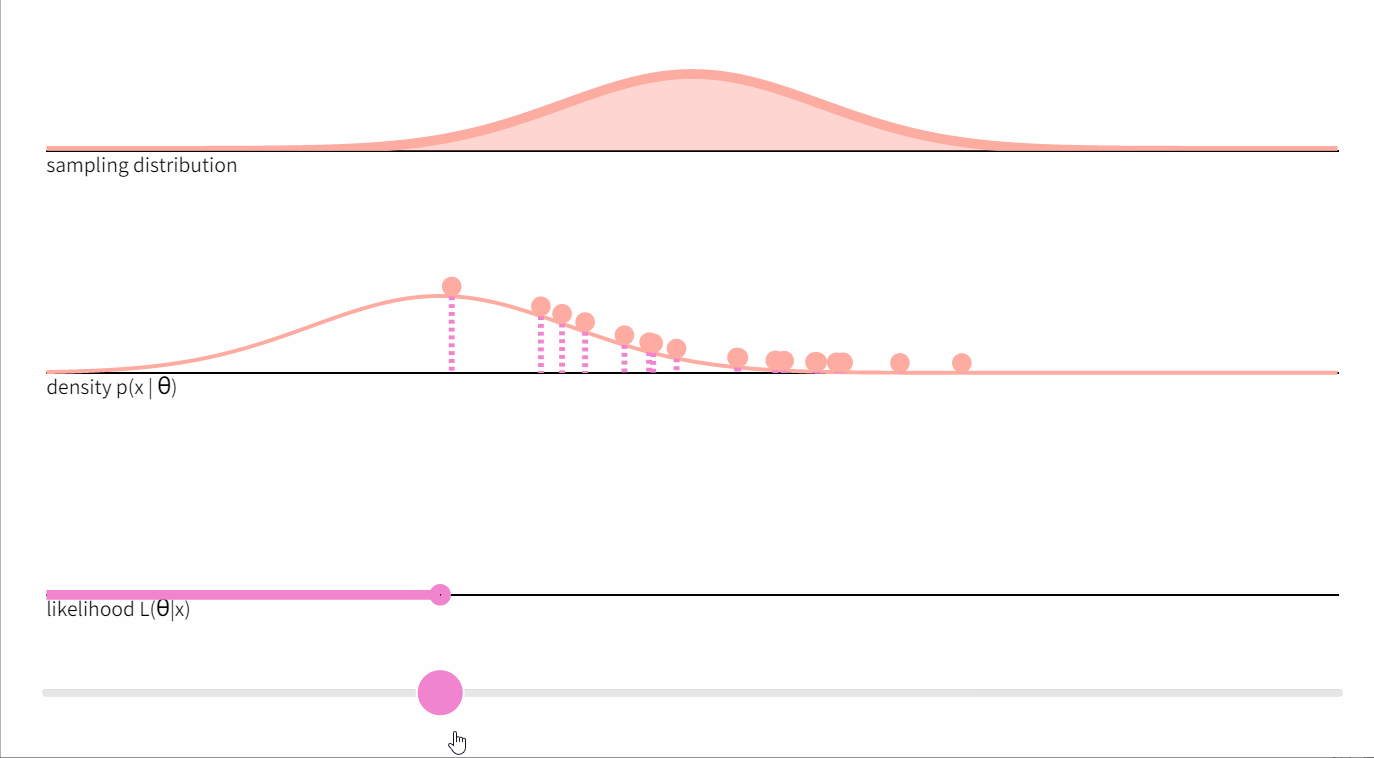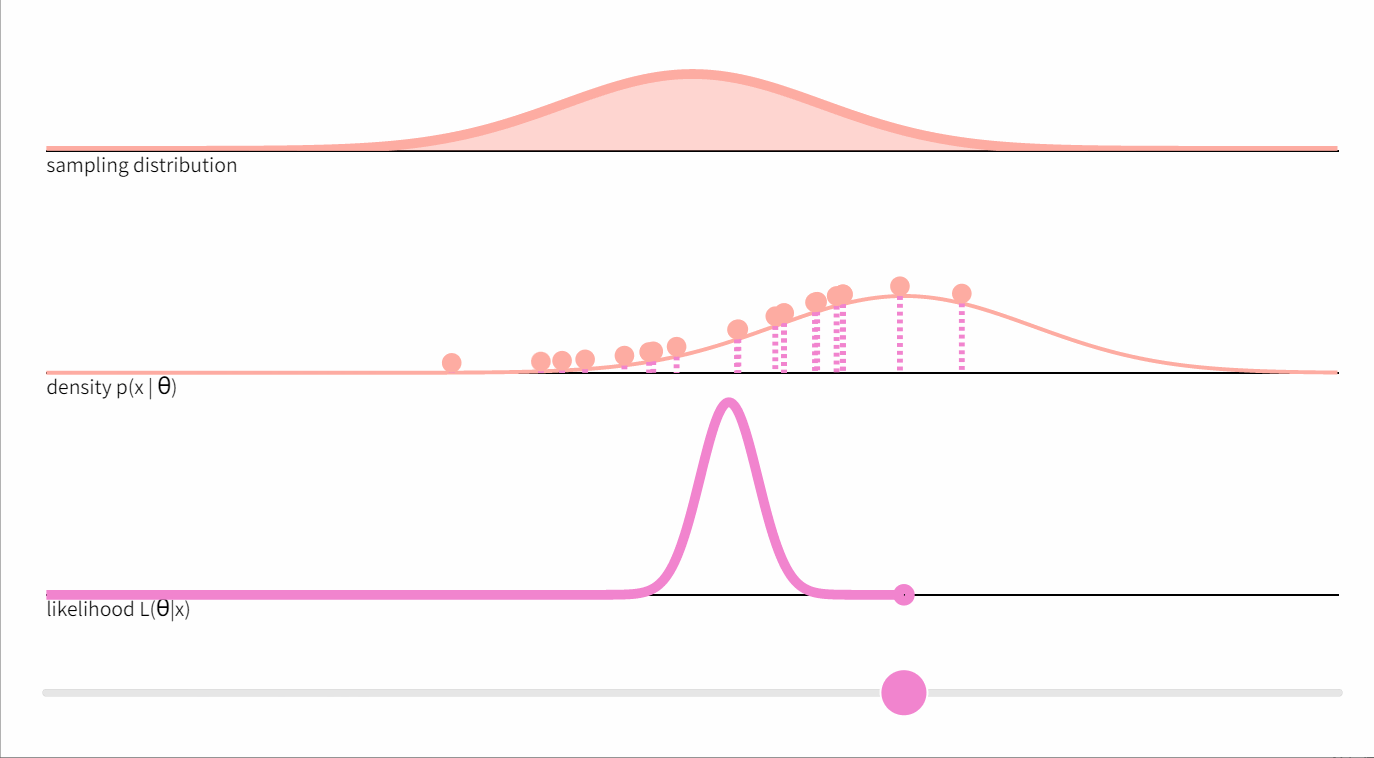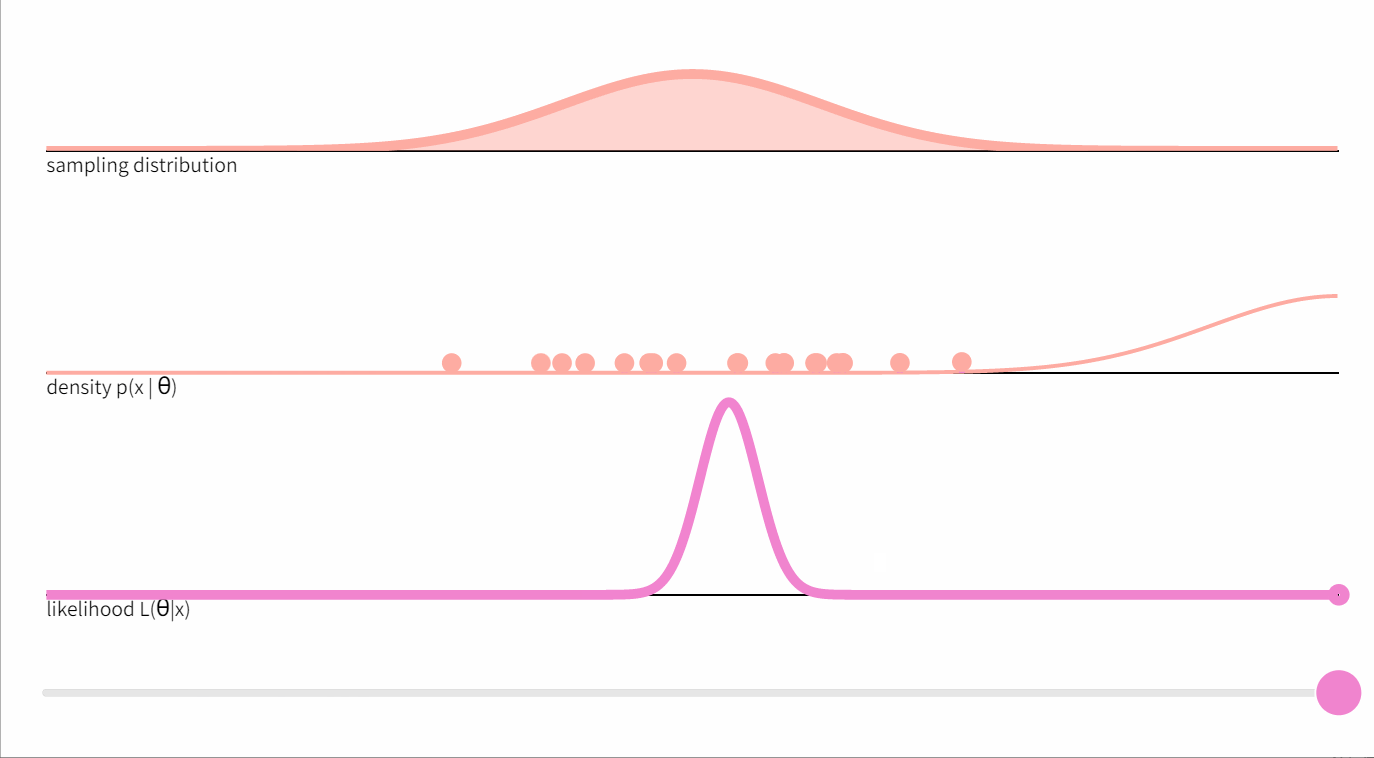
下图显示了从标准正态分布中抽取的20个点的随机样本 $x$ ，以及均值参数的相应似然函数

一般来说，给定一个由 $n$ 个独立和来自相同分布 $P(X|\theta )$ 的随机变量 $X_1,..,X_n$ ，其似然函数为
$$\begin{array}{rl}L(\theta |X_1,..,X_n)& =P(X_1,..,X_n|\theta )\\ & =\prod _{i=1}^{n}P(X_i|\theta )\end{array}$$
在方差为1、均值为未知的正态分布的情况下，这个方程提出了一种可视化似然函数如何产生的方法。想象一下，通过逐渐增加 $\theta$，将$N(\theta ，1)$分布的概率密度函数从左到右滑动。当我们遇到每个样本 $X_i$ 时，密度函数将该点从X轴上 “抬起”。上图中间部分的虚线代表数 $P(Xi|\theta )$。它们的乘积正是似然值。

我们可以看到，似然值的最大化是由 $N(\theta ，1)$ 分布的密度能够将最多的点从$x$轴上抬起来的 $\theta$ 值决定的。可以证明，这个最大化的值是由样本平均值给出的
$$\overline{X}=\frac{1}{n}\sum _{i=1}^n{X}_i$$
在这种情况下，我们假设样本均值是参数 $\theta$ 的最大似然估计量。

在贝叶斯推断中，似然性用于量化一组数据 $X$ 支持特定参数值 $\theta$ 的程度。基本思想是，如果数据可以由给定的参数值 $\theta$ 以高概率生成，那么这样的 $\theta$ 值在数据眼中是有利的。

最大似然估计是一种估计模型参数的方法，目的在于透过真是观察到的样本信息，找出最有可能产生这些样本结果的模型参数。

后验Posterior

贝叶斯推理的目标是通过考虑我们观察到的数据 $X$ 来更新我们的先验信念 $P(\theta$ )。这个推理过程的最终结果是后验分布 $P(\theta |X)$ 。贝叶斯定理指定了计算后验的方法，
$$P(\theta |X)=\frac{P(X|\theta )P(\theta )}{P(X)}$$
由于在任何特定的推理问题中，数据是固定的，我们通常只对 $\theta$ 的函数项感兴趣。因此，贝叶斯定理的本质是
$$P(\theta |X)\propto P(X|\theta )P(\theta )$$
简而言之
$$后验概率\propto 似然值\times 先验概率$$

从先验概率到后验概率

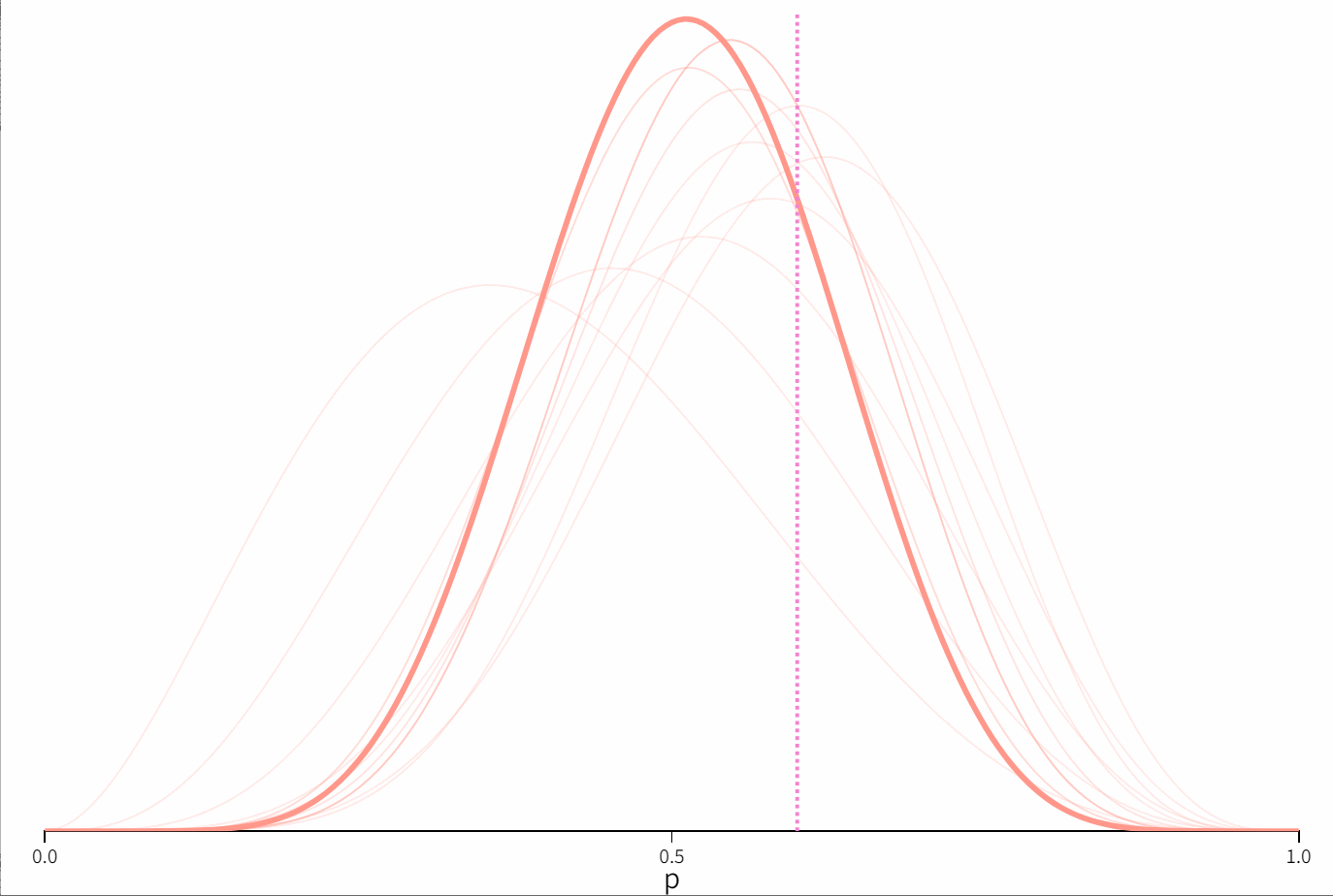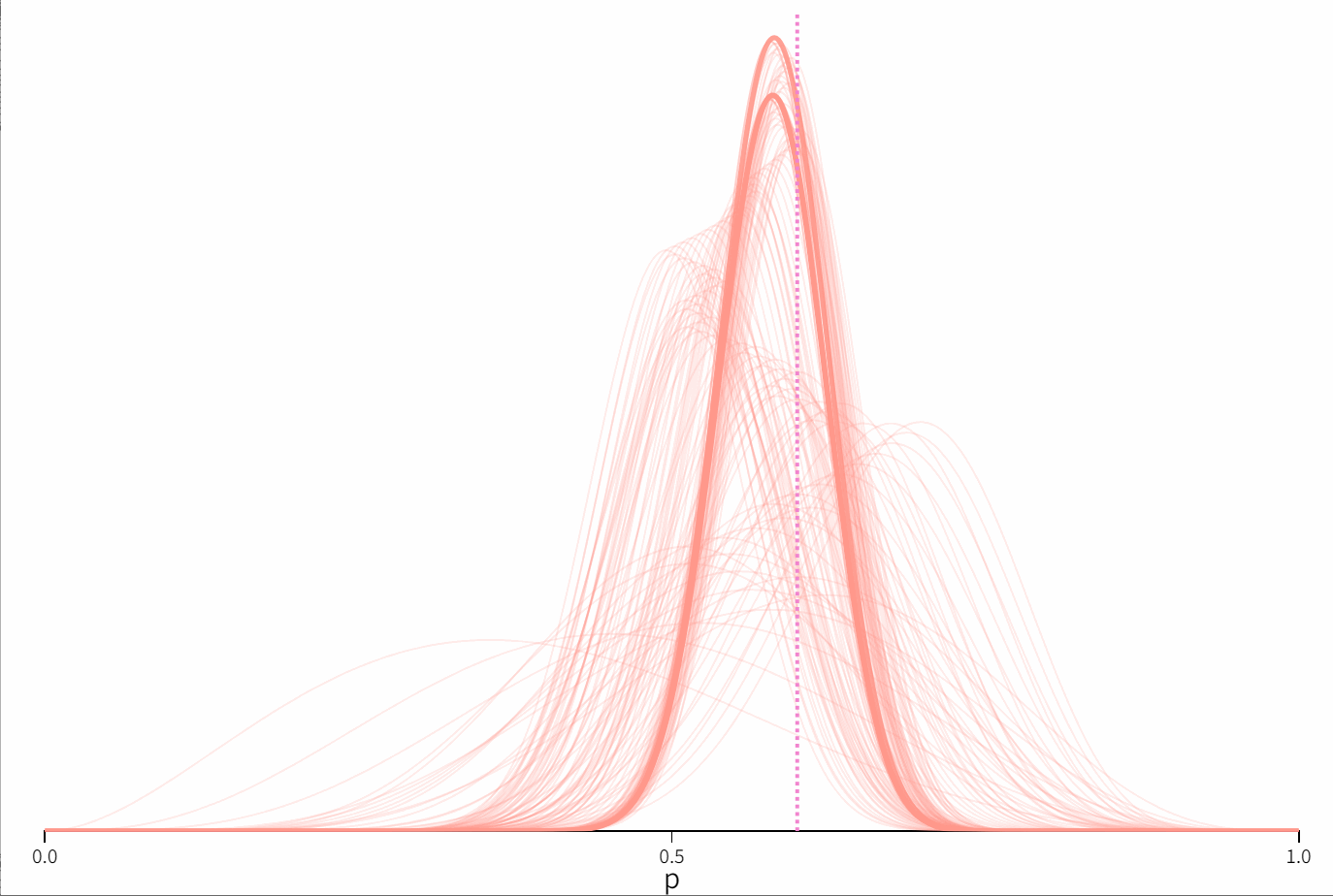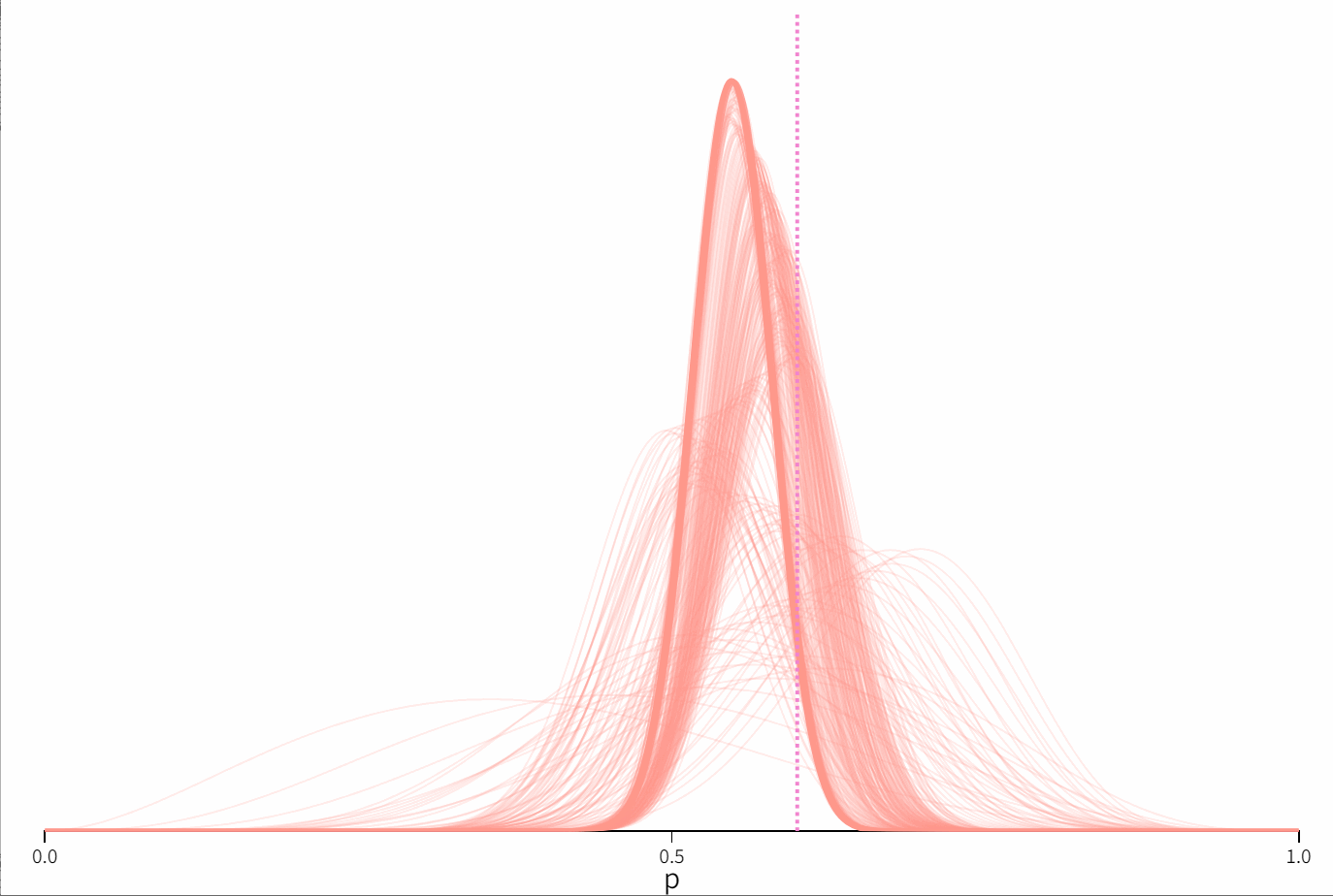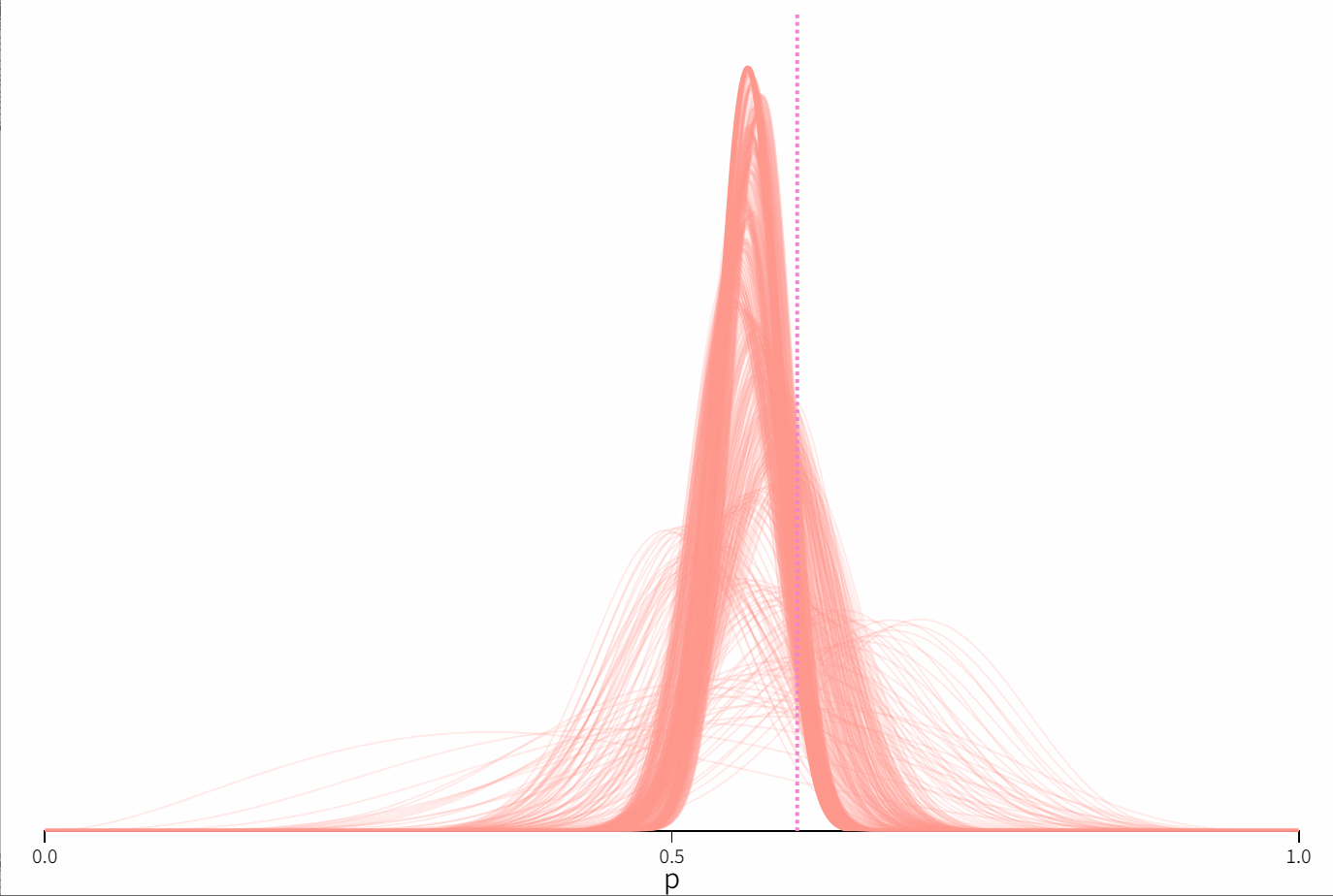
贝叶斯统计的核心思想是利用观察到的数据来更新先验信息。考虑一枚不均匀的硬币，抛出正面的概率为 $p$。这里我们设置为0.6。

这里我们假定 $p$ 的先验分布是 $Beta(\alpha ,\beta )$，在图中粉色曲线代表了先验概率的密度分布函数。这里我们设置为$\alpha =3.07,\beta =4.65$。

当我们重复抛硬币时，我们不断更新关于 $p$ 的后验分布。这个后验分布就是我们对 $p$ 的最好估计，同时这也是我们相对我们下一次抛硬币结果的先验信息。

参考

1. https://github.com/seeingtheory/Seeing-Theory