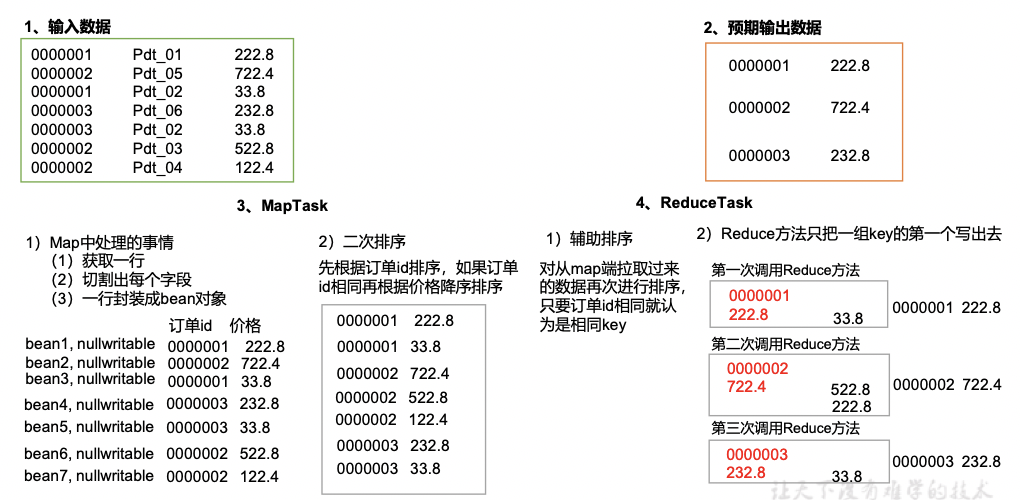
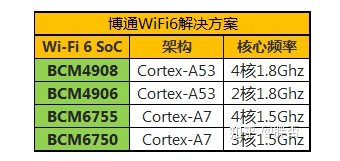
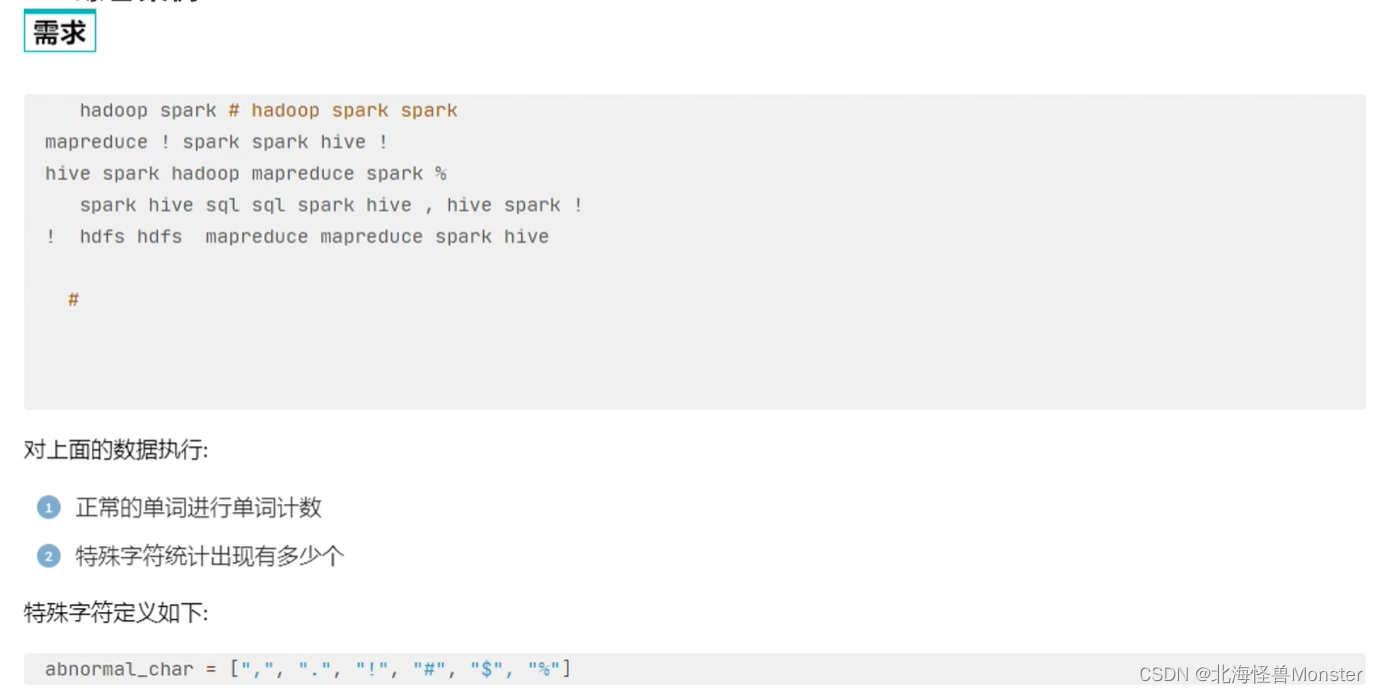
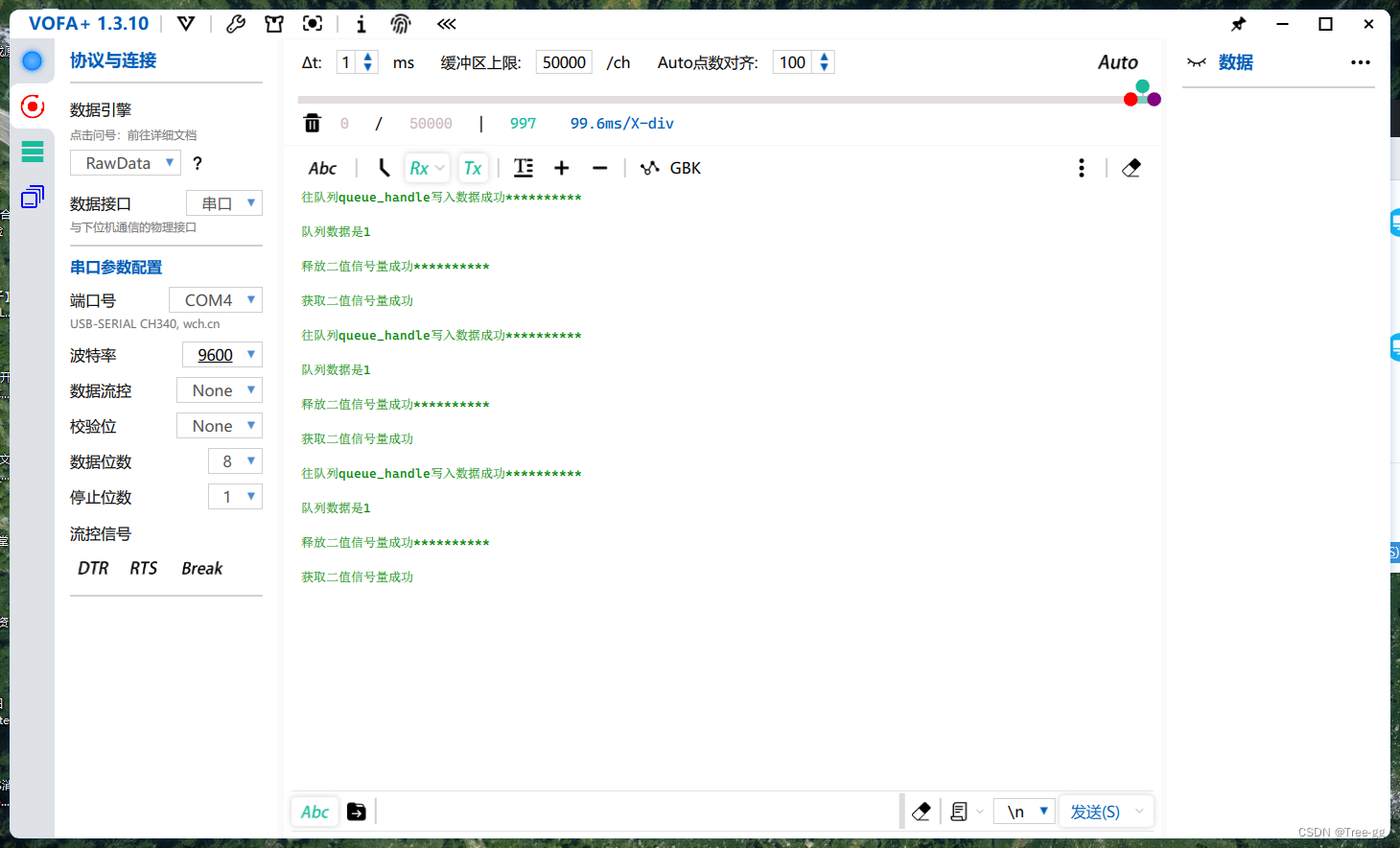
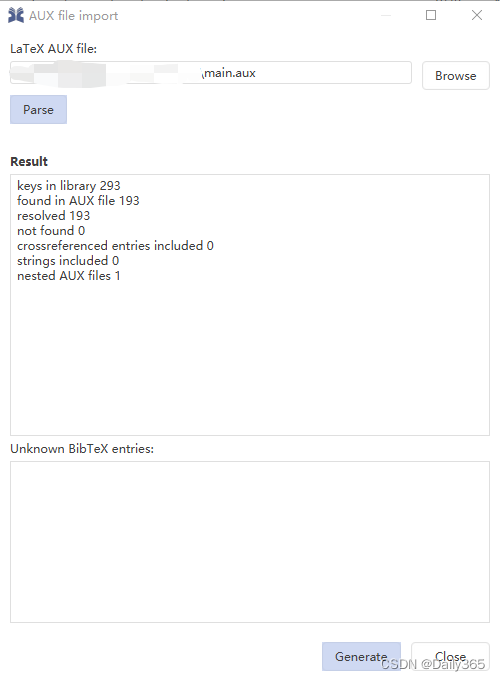
冒泡排序思想
基本思想: 冒泡排序,类似于水中冒泡,较大的数沉下去,较小的数慢慢冒起来(假设从小到大),即为较大的数慢慢往后排,较小的数慢慢往前排。
直观表达, 每一趟遍历,将一个最大的数移到序列末尾。
下图演示排序流程:
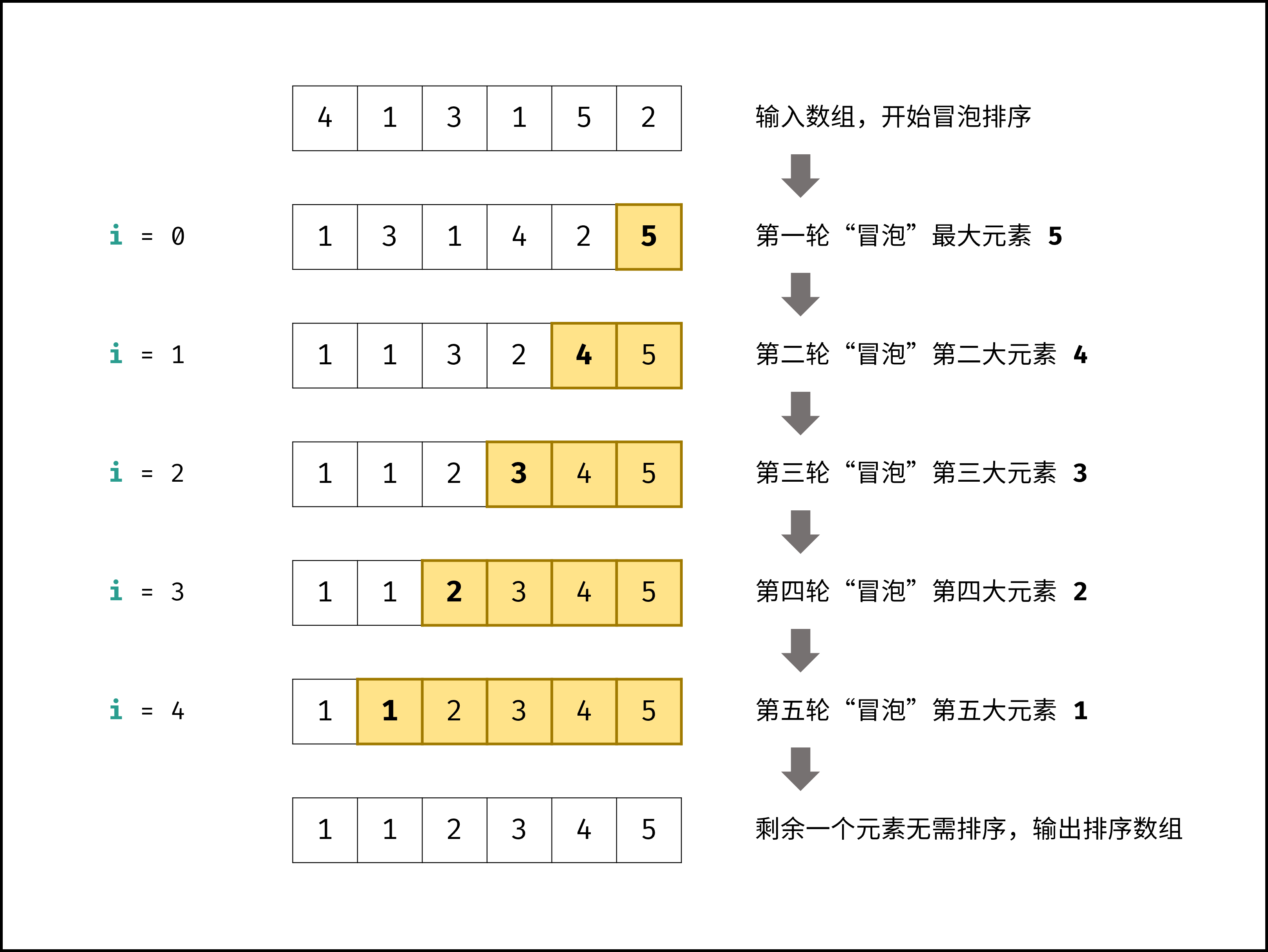
下面是传统冒泡排序写法 时间复杂度O(n^2):
public static void bubbleSort(int[] nums) {
int length = nums.length;
for (int i = 0; i < length; i++) {
System.out.println("i=" + i);
for (int j = 0; j + 1 < length -i; j++) {
System.out.println("内层循环次数:====================-" + j);
if (nums[j] > nums[j + 1]) {
int tem = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tem;
}
}
System.out.println("=======第" + i + " 轮外循环执行==============================");
for (Integer integer : nums) {
System.out.println(integer);
}
}
}执行下看看效果:



第一轮 5次 ,第二轮 4次,第三轮 3次, 第四轮 2次 ,第五轮 1次 ,第六轮0次
但是当我们遇到下面这种序列
即: 1,2,3,5,4 我们只需要排一趟就可以了 而无需后续的循环。
初次优化:
基于这种情况我们给出了下面这种优化。
通过增加一个标志位 flag ,若在某轮「内循环」中未执行任何交换操作,则说明数组已经完成排序,直接返回结果即可。
public static void bubbleSort1(int[] nums) {
int length = nums.length;
//定义标志位标记已经有序或无序
boolean flag = false;
for (int i = 0; i < length; i++) {
System.out.println("i=" + i);
flag = true;
for (int j = 0; j + 1 < length - i; j++) {
System.out.println("内层循环次数:====================-" + j);
if (nums[j] > nums[j + 1]) {
int tem = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tem;
//交换后对flag置false,表示已经处理成有序
flag = false;
}
}
// 已经排好序了 无需后续循环了
if (flag) {
break;
}
System.out.println("=======第" + i + " 轮外循环执行==============================");
for (Integer integer : nums) {
System.out.println(integer);
}
}
}在看下执行效果:

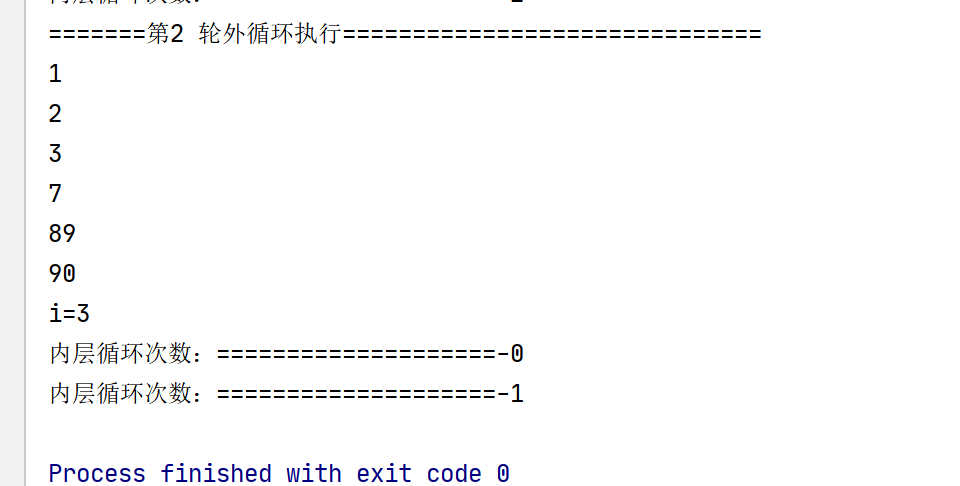
第一轮 5次 ,第二轮 4次,第三轮 3次 ,第四轮 2次
很明显外层减少了循环次数
优化后的冒泡排序的最差和平均时间复杂度仍为 O(N^2) ;在输入数组 已排序 时,达到 最佳时间复杂度 O(N) 。
继续优化:
然而这种优化只能做到某一次已经排好序的时候我们直接跳跳出来,基于第一种优化我们得到一种启发:当一个数组接近有序的时候我们往往只需要在某一个小范围内排序即可,我们可以用一个标记来表示这个范围的下限,例如遇到下面的情况
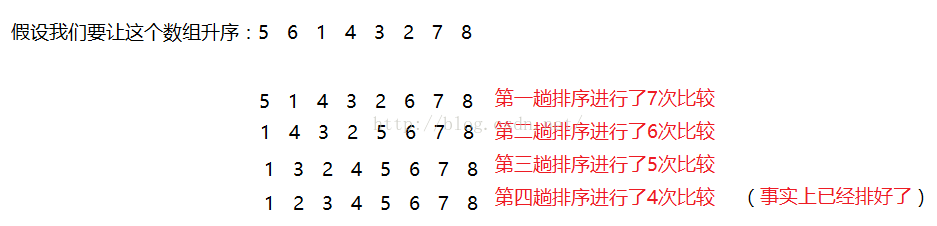
然而我们发现,每次排序前或排序后数组的后面都有一部分已经有序,这时我们只要记下最后一次排下的数组的下标,下次排序的时候就可以只排序到此下标位置即可

目的就是减少内层循环比较的次数
public static void bubbleSort2(int[] nums) {
int length = nums.length;
int index = length;
//每一次我们找到无序区的上界
int maxIndex = 0;
//定义标志位标记已经有序或无序
boolean flag = false;
for (int i = 0; i < length; i++) {
System.out.println("i=" + i);
flag = true;
for (int j = 0; j + 1 < index; j++) {
System.out.println("内层循环次数:====================-" + j);
if (nums[j] > nums[j + 1]) {
int tem = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tem;
//交换后对flag置false,表示已经处理成有序
flag = false;
//注意不要在这里直接将index置为j
maxIndex = j + 1;
}
}
// 已经排好序了 无需后续循环了
if (flag) {
break;
}
//若排序过则将index置为最后一次交换的坐标,若没有则表示已经有序
index = maxIndex;
System.out.println("=======第" + i + " 轮外循环执行==============================");
for (Integer integer : nums) {
System.out.println(integer);
}
}
}再次执行看看效果:


第一轮 5次 ,第二轮 3次,第三轮 2次 ,第四轮 1次
很明显内层循环也减少了很多
优化后的冒泡排序的最差和平均时间复杂度仍为 O(N^2) ;在输入数组 已排序 时,达到 最佳时间复杂度 O(1) 。
其实还可以再优化, 一层外循环 执行2个同级的内循环( 正着扫描得到最大值, 反着扫描得到最小值)
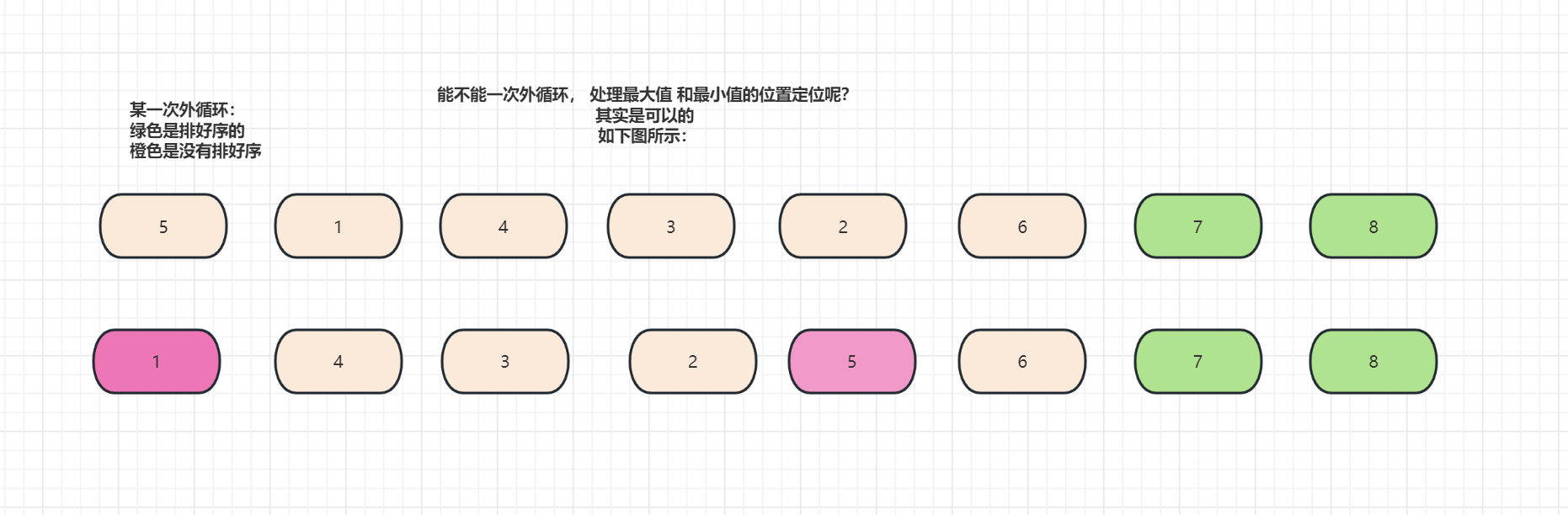
总结
主要从以下2方面优化了传统的冒泡排序写法
// 1、减少外层循环次数
// 2、减少内层循环次数