一.流程
1.建立评价体系
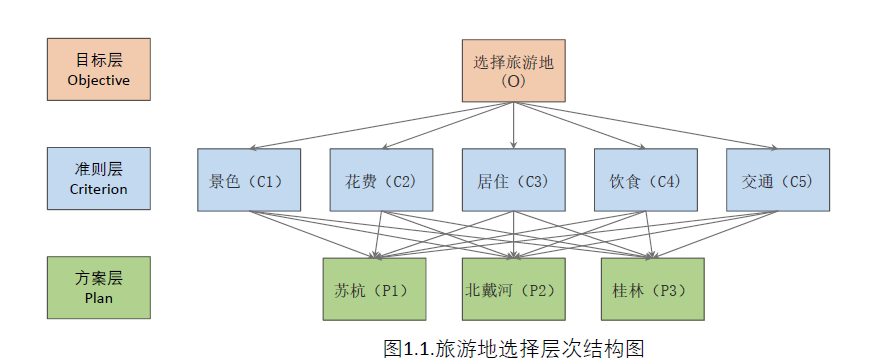
2.建立判断矩阵
2.1 A-C-C矩阵
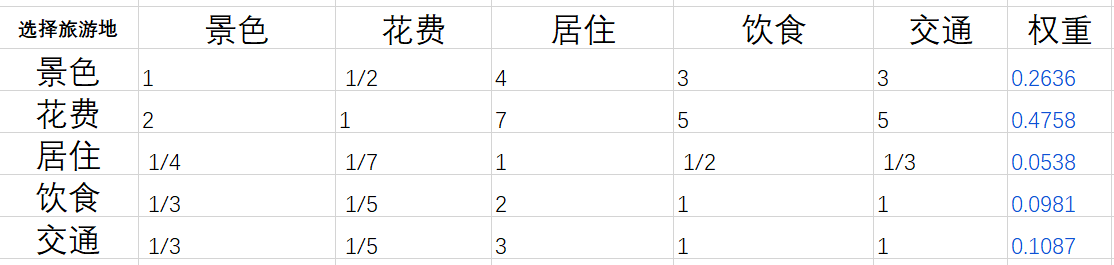
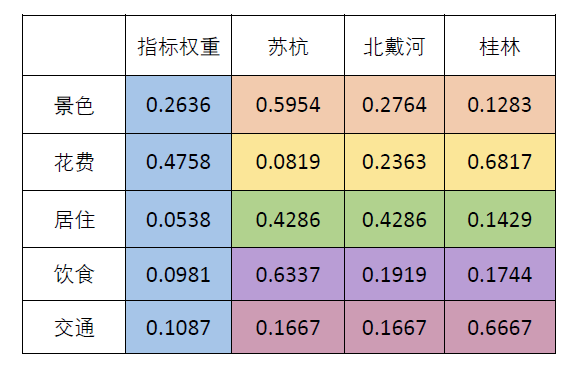
从准则层对目标层的特征向量上看,花费的权重最大
算术平均法求权重的结果为:
0.2623
0.4744
0.0545
0.0985
0.1103
几何平均法求权重的结果为:
0.2636
0.4773
0.0531
0.0988
0.1072
特征值法求权重的结果为:
0.2636
0.4758
0.0538
0.0981
0.1087
一致性指标CI=
0.0180
一致性比例CR=
0.0161
因为CR<0.10,所以该判断矩阵A的一致性可以接受!
2.2 Ci-P-P矩阵

从方案层对目标层的权重上看,桂林的权重最大(以C层最大的花费为Ci,两层权重的乘积)
算术平均法求权重的结果为:
0.5949
0.2766
0.1285
几何平均法求权重的结果为:
0.5954
0.2764
0.1283
特征值法求权重的结果为:
0.5954
0.2764
0.1283
一致性指标CI=
0.0028
一致性比例CR=
0.0053
因为CR<0.10,所以该判断矩阵A的一致性可以接受!
3.计算评分及排序
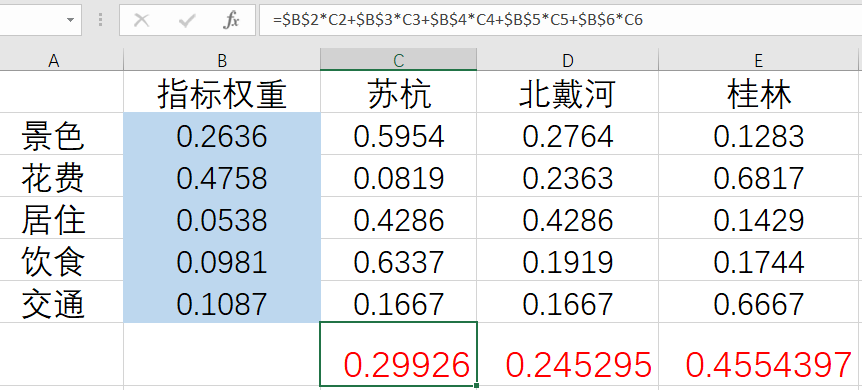
计算:
fn+F4锁定单元格
排序:
选择性粘贴:数值
粘贴中转置,再排序
二.论文
考虑到层次分析法构造时的主观色彩比较强,我们又利用熵值取权法给出了客观条件下的一组权值w2,对w1进行修正
通过判断各个因素的变化剧烈程度来决定该因素在最终目标中所占的权重
比如国家的财政支持对高等院校的学费的制定影响很重要,但是如果财政支持费用10年都不变,而家庭支付承受能力虽然对学费的制定没有国家财政支持的影响那么重要,但是它每年都在快速的增加,从熵值取权法的角度来看这时家庭的支付承受能力的影响就比国家财政的支持大,这与客观的人们的想法也是一样,同时它和层次分析法得出的结论是互补的且是客观的。
我们利用熵值取权法客观地给出一个5个因素的1×5的权重矩阵w2,对由层次分析法给出的1×5的权重矩阵w1,以0.2:0.8的比例进行修正,从而给出最终的5个因素对合理化指数的组合权重值阵 W=0.8×w1+0.2×w2



![[数据结构]---八大经典排序算法详解](https://img-blog.csdnimg.cn/0e8142407d4d4211b8615f4750ab6a65.png#pic_center)
![SpringCloud系列(十三)[分布式搜索引擎篇] - ElasticSearch 的概念及 Centos 7 下详细安装步骤](https://img-blog.csdnimg.cn/d5befcf1c15f489d8d23b861827c13c5.png#pic_center)