[数据结构]---八大经典排序算法详解

news2024/9/24 1:23:23

在这里插入图片描述

🐧作者主页：king&南星
🏰专栏链接：c++

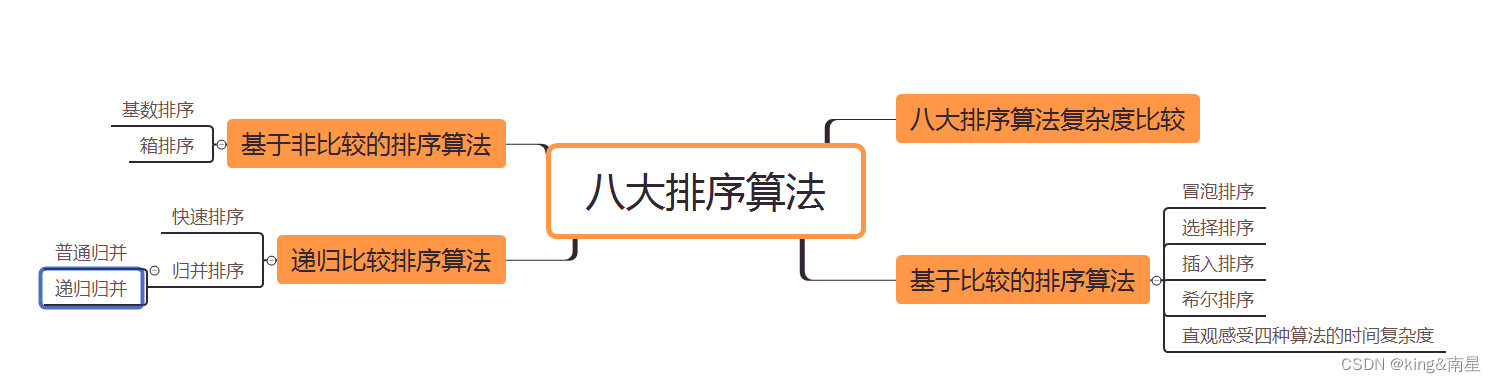
在这里插入图片描述
在这里插入图片描述

文章目录

      • 一、八大排序算法复杂度对比
      • 二、基于比较的排序算法
        • 1.冒泡排序
        • 2.选择排序
        • 3.插入排序
        • 4.希尔排序
        • 5.直观感受四种算法的时间复杂度
      • 三、基于非比较的排序算法
        • 1.基数排序
        • 2.箱(桶)排序
      • 四、递归比较排序算法
        • 1.快速排序
        • 2.归并排序
          • 1.普通归并
          • 2.归并递归

一、八大排序算法复杂度对比

在这里插入图片描述

二、基于比较的排序算法

1.冒泡排序

  • 介绍：冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。

它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行，直到没有相邻元素需要交换，也就是说该元素列已经排序完成。

这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样，故名“冒泡排序”

  • 核心：

    冒泡排序:
    比较 NUM-1轮，每轮NUM-1次，
    每轮（相邻两个比较，不符合要求则交换）
    找出一个最大的或者一个最小的
    在这里插入图片描述

//冒泡排序
void bubble_sort(int* a, int len)
{
    int t;
    for ( int i = 0;  i < len-1;  i++)          //len-1轮
    {
        for( int j = 0; j < len-1-i ; j++ )     //每轮为无序的元素个数-1次
        {
            if ( a[j] > a[j+1] )               //不符合规则交换
            {
                t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
            }
        }
    }
}

总结：

  1. 冒泡排序是一种非常容易理解的排序
  2. 时间复杂度：O( N2)
  3. 空间复杂度：O(1)
  4. 稳定性：稳定

2.选择排序

  • 介绍：选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

  • 核心：

    选择排序：

    ​ 先假设待排数组第一个为最小值

    ​ 选择NUM-1轮，每轮从待排数组中选最小的，与第一个进行比较，决定放不放到待排数组第一个
    ​ 循环从待排数组中找到最小的，记录其下标
    ​ 交换

在这里插入图片描述

//选择排序
void select_sort(int* a, int len)
{
    int t;
    int minIndex;
    for (int i = 0; i < len-1; i++)  //len-1轮
    {
        //从待排数组中(i ----- len-1)找到最小的
        minIndex = i;      //先假设待排数组中的第一个最小
        for (int j = i+1; j < len; j++)
        {
            minIndex = a[j] > a[minIndex] ? minIndex : j;
        }
        //符合条件和待排数组中的第一个元素(i)交换
        if ( a[minIndex] < a[i] )
        {
            t = a[minIndex];
            a[minIndex] = a[i];
            a[i] = t;
        }
    }
}

总结：

  1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
  2. 时间复杂度：O(N2)
  3. 空间复杂度：O(1)
  4. 稳定性：不稳定

3.插入排序

  • 介绍：插入排序，一般也被称为直接插入排序。对于少量元素的排序，它是一个有效的算法 。插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增1的有序表。在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。

    核心：

    插入排序：
    设置第一个为有序数组，右边NUM-1个为待插数据
    然后NUM-1轮，每轮把一个数据插入到有序数组中
    插入方式：
    1. 先临时保存待插数据
    2. 然后从待插数据前一个开始往前循环（越界循环结束）
    比待插数据大则往后覆盖，比待插数据小则循环结束
    3. 用待插数据覆盖回来（第二步结束后下标的下一个位置）

在这里插入图片描述

插入部分图解
在这里插入图片描述

//插入排序
void insert_sort(int* a, int len)
{
    int j;
    int temp;//保存待插数据
    for (int i = 1; i < len; i++) //len-1轮
    {
        temp = a[i]; 
        //待插数据前一个开始往前循环（越界循环结束）
        for ( j = i-1 ; j >= 0 ; j-- ) 
        {
            //比待插数据大则往后覆盖
            if ( a[j] > temp )  a[j + 1] = a[j];
            else break;
        }
        //用待插数据覆盖回来（第二步结束后下标的下一个位置）
        a[j + 1] = temp;
    }
}

总结：

  1. 元素集合越接近有序，直接插入排序算法的时间效率越高
  2. 时间复杂度：O(N2)
  3. 空间复杂度：O(1)，它是一种稳定的排序算法
  4. 稳定性：稳定

4.希尔排序

  • 介绍：

  • 希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。

    希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。

    核心：

    希尔（shell）排序：
    一个叫做shell的科学家发明的
    优化后的插入排序
    引入步长的概念：
    一开始是 len/2 然后每次 除2 到1为止
    根据步长来分组，然后组内作插入排序

在这里插入图片描述

//希尔排序
void shell_sort(int* a, int len)
{
    int j, temp;
    int step = len >> 2;
    while ( step )//根据步长来分组
    {
        //组内作插入排序
        //从step开始  len-1-step轮
        for( int i = step ; i < len; i++ )
        {
            temp = a[i];//临时保存待插数据
            //待插数据前一个开始往前循环（越界循环结束）
            for ( j = i-step; j >= 0 ; j -= step )
            {
                //比待插数据大则往后覆盖
                if (a[j] > temp) a[j + step] = a[j];
                else break;
            }
            //用待插数据覆盖回来（第二步结束后下标的下一个位置）
            a[j + step] = temp;
        }
        step >>= 1;
    }
}

总结：

  1. 希尔排序是对直接插入排序的优化。
  2. 当step > 1时都是预排序，目的是让数组更接近于有序。当step == 1时，数组已经接近有序的 了，这样就会很快。这样整体而言，可以达到优化的效果。
  3. 希尔排序的时间复杂度不好计算，需要进行推导，推导出来平均时间复杂度： O(N1.3— N2）
  4. 稳定性：不稳定

5.直观感受四种算法的时间复杂度

这里随机产出100000个数字，利用上面4种排序算法进行排序，结果如下，可以看到希尔排序仅仅用了16ms

在这里插入图片描述

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include <windows.h>
//数据个数
#define NUM  100000

void init(int* a, int len);
void bubble_sort(int* a, int len);
//选择排序
void select_sort(int* a, int len);
//插入排序
void insert_sort(int* a, int len);
//希尔排序
void shell_sort(int* a, int len);

int main() {
    ULONGLONG oldTime, newTime;
    srand(time(NULL));
    int arr[NUM];
    init(arr, NUM);//初始化
    //获取排序前时间
    oldTime = GetTickCount64();
    bubble_sort(arr, NUM);//排序
    //获取排序后时间
    newTime = GetTickCount64();
    printf("bubble_sort:%llu\n", newTime - oldTime);

    init(arr, NUM);
    oldTime = GetTickCount64();
    select_sort(arr, NUM);
    newTime = GetTickCount64();
    printf("select_sort:%llu\n", newTime - oldTime);

    init(arr, NUM);
    oldTime = GetTickCount64();
    insert_sort(arr, NUM);
    newTime = GetTickCount64();
    printf("insert_sort:%llu\n", newTime - oldTime);


    init(arr, NUM);
    oldTime = GetTickCount64();
    shell_sort(arr, NUM);
    newTime = GetTickCount64();
    printf("shell_sort:%llu\n", newTime - oldTime);
    while (1);
    return 0;
}
void init(int* a, int len) {
    for (int i = 0; i < len; i++)
        a[i] = rand() % 1000;
}
//希尔排序
void shell_sort(int* a, int len) {
    int step = len / 2;
    int temp;
    int j;
    while (step) {//分组
        //组内做插入排序
        for (int i = step; i < len; i++) {//每次循环插入a[i]
            temp = a[i];//临时存储待插数据
            for (j = i - step; j >= 0 && a[j] > temp; j -= step) {//从前往后覆盖
                a[j + step] = a[j];
            }
            a[j + step] = temp;
        }


        step /= 2;//每次步长变成原来的一半
    }
}

//插入排序
void insert_sort(int* a, int len) {
    int temp;
    int j;
    for (int i = 1; i < len; i++) {//每次循环插入a[i]
        //把a[i] 插入到 a[0] - a[i-1] 数组中去

        temp = a[i];//临时存储待插数据

        for (j = i - 1; j >= 0 && a[j] > temp; j--) {//从前往后覆盖
            a[j + 1] = a[j];
        }
        //插入进来
        a[j + 1] = temp;

    }
}
//选择排序
void select_sort(int* a, int len) {
    int min_idx;//记录最小的元素的下标
    int temp;
    for (int i = 0; i < len - 1; i++) {//找len-1次
        //每次 找出  a[i] - a[len-1] 范围内最小的元素 
        min_idx = i;//假设a[i]最小
        for (int j = i; j < len; j++) {
            min_idx = ((a[min_idx] < a[j]) ? min_idx : j);
        }
        //a[min_idx] 和 a[i]交换
        temp = a[i];
        a[i] = a[min_idx];
        a[min_idx] = temp;
    }
}

void bubble_sort(int* a, int len) {
    int temp;
    for (int j = 0; j < len - 1; j++) {
        for (int i = 0; i < len - j - 1; i++) {//0 - len-2
            if (a[i] > a[i + 1]) {//不符合要求
                //交换
                temp = a[i];
                a[i] = a[i + 1];
                a[i + 1] = temp;
            }
        }
    }
}

三、基于非比较的排序算法

1.基数排序

  • 介绍：基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog®m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

    核心：

    基数排序 ：O(n)
    最快的排序方式 没有之一
    利用数组下标天然有序的特性来进行排序
    max:最大元素值
    限制很多：

    1. 只能排正整数（优化后可以对所有整数排序）
2. 不能有重复
3. 空间可能耗费特别大
4. 临时空间大小

在这里插入图片描述

//基数排序
void radix_sort(int* a, int len, int max)
{
    int index = 0;
    //先准备一个临时数组 max+1
    int* pTemp = (int*)malloc(sizeof(int) * (max + 1));
    assert(pTemp); //判断申请成功没
    //初始化为-1//for (int i = 0; i <= max; i++) pTemp[i] = -1;
    memset(pTemp, -1, sizeof(int) * (max + 1));
    //将待排数组放到临时数组中，待排数组的值作为临时数组的下标
    for (int i = 0; i < len; i++) pTemp[a[i]] = a[i];
    //从临时数组中把排序好的数据放回原数组中
    for (int i = 0; i <= max; i++) 
    {
        if ( pTemp[i] != -1 )
        {
            a[index++] = pTemp[i];
        }
    }
    //释放内存
    free(pTemp);
}

总结：

  1. 时间复杂度：O（n+k）
  2. 空间复杂度：O（n+k）
  3. 不能对小数进行排序，但是速度极快

2.箱(桶)排序

  • 介绍：桶排序 (Bucket sort)或所谓的箱排序，是一个排序算法，工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候，桶排序使用线性时间（Θ（n））。但桶排序并不是 比较排序，他不受到 O(n log n) 下限的影响。

    核心：

    桶(箱)排序:bucket_sort
    把数据分成若干个箱子 然后箱子里用其他排序

在这里插入图片描述

这里是按个位十位分箱，内部类似于基数排序

//箱排序
void bucket_sort(int* a, int len)
{
    int idx, k;
    int n = 1; 
    int* pTemp = NULL;
    while ( n < AREA )//1000以内的数字，AREA ==1000
    {
        //1 做箱子  并初始化箱子
        pTemp = (int*)malloc(10 * len * sizeof(int));
        for (int i = 0; i < 10 * len; i++) pTemp[i] = -1;
        //2 根据特性(对应位作为箱子的编号)放入箱子中
        for (int i = 0; i < len; i++)
        {
            //获取到数据这一轮要看的位上的数据
            idx = a[i] / n % 10;
            pTemp[idx * len + i] = a[i];
        }
        //3 从箱子中取出，覆盖a数组
        k = 0;
        for (int i = 0; i < 10*len; i++)
        {
            if ( pTemp[i] != -1 )
                a[k++] = pTemp[i];
        }
        //4 销毁箱子
        free(pTemp);
        pTemp = NULL;
        n *= 10;
    }
}

四、递归比较排序算法

1.快速排序

  • 介绍：快速排序（Quicksort），计算机科学词汇，适用领域Pascal，c++等语言，是对冒泡排序算法的一种改进。

    核心：

    快速排序：就是分组排序
    把数据分成两组
    确定中间值，左边都比中间值小 右边都比中间值大
    递归(递推)持续分组 到 不可再分(一组只有一个数据)为止

在这里插入图片描述

void Quick_sort(int* a, int len)
{
    quick_sort(a, 0, len - 1);
}
void quick_sort(int* a, int Left, int Right)
{
    int L = Left, R = Right;
    if ( L >= R ) return; //递归结束
    // 先假设a[left]是中间数据,并临时保存
    int temp = a[L];
    // 循环挪动l和r并覆盖  循环结束后 L==R
    while ( L < R )
    {
        // 先挪右边的
        while ( L < R && a[R] > temp)   R--;
        a[L] = a[R];
        // 再挪左边的
        while (L<R && a[L] < temp )    L++;
        a[R] = a[L];
    }
    // 用中间数据覆盖回来
    a[L] = temp; //a[R] = temp;
    quick_sort(a, Left, R - 1);
    quick_sort(a, L + 1, Right);
}

2.归并排序

  • 介绍：归并排序是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
1.普通归并
  • 核心：两个有序数组合并成一个有序数组

在这里插入图片描述

void Merge_sort(int* a, int L, int M, int R)
{
    int Left = L, Right = M + 1;
    if (L >= R) return;
    //开临时内存
    int* pTemp = (int*)malloc(sizeof(int) * (R - L + 1));
    int k = 0;
    //两个中有一个放完了
    while ( Left <= M && Right <= R )
    {
        if (a[Left] < a[Right]) pTemp[k++] = a[Left++];
        else pTemp[k++] = a[Right++];
    }
    //左边还没放完
    if (Left <= M) memcpy(pTemp + k, a + Left, sizeof(int) * (M - Left + 1));
    //右边还没放完
    else  memcpy(pTemp + k, a +Right, sizeof(int) * (R - Right + 1));
    //覆盖回去
    memcpy( a + L , pTemp, sizeof(int) * (R - L + 1));
    //释放内存
    free(pTemp);
}
2.归并递归
  • 核心：把无序数组完全拆开，再进行归并排序

在这里插入图片描述

void Merge_Sort(int* a, int len)
{
    merge__sort(a, 0, len - 1);
}
void merge__sort(int* a, int L, int R)
{
    // L和R不相等，说明还没拆到只剩一个，继续拆
    if (L < R)
    {
        int m = L + (R - L) / 2;
        merge__sort(a, L, m);        //左边一半
        merge__sort(a, m + 1, R);    //右边一半
        Merge_sort(a, L, m, R);      //拆到无法拆了就合并
    }
}

🎉欢迎各位→点赞👏 + 收藏💞 + 留言🔔​
💬总结：希望你看完之后，能对你有所帮助，不足请指正！共同学习交流 🐾

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/355344.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL 实战记录篇

MySQL 实战记录篇

记录一下在MySQL实战中简单的笔记 MySQL的逻辑架构&#xff0c;一条查询语句是怎么执行的&#xff1f; MySQL 的架构共分为两层&#xff1a;Server 层和存储引擎层 简单的架构图&#xff1a; 连接器&#xff1a;用来和mysql服务器建立连接&#xff0c;tcp三次握手&#xff0…
阅读更多...
SpringCloud系列（十三）[分布式搜索引擎篇] - ElasticSearch 的概念及 Centos 7 下详细安装步骤

SpringCloud系列（十三）[分布式搜索引擎篇] - ElasticSearch 的概念及 Centos 7 下详细安装步骤

打开淘宝, 搜索 狂飙 会出现各种价格有关狂飙的书籍, 当然也有高启强同款的孙子兵法!!! 如下图所示: 那么面对海量的数据, 如何快速且准确的找到我们想要的内容呢? 淘宝界面已经可以按照综合排序 / 销量 / 信用 / 价格等进行筛选, 是如何做到的呢? ElasticSearch 11 Elastic…
阅读更多...
实战一（下）：如何利用基于充血模型的DDD开发一个虚拟钱包系统？

实战一（下）：如何利用基于充血模型的DDD开发一个虚拟钱包系统？

上一节课,我们做了一些理论知识的铺垫性讲解,讲到了两种开发模式,基于贫血模型的传统开发模式,以及基于充血模型的DDD开发模式。今天&#xff0c;我们正式进入实战环节&#xff0c;看如何分别用这两种开发模式&#xff0c;设计实现一个钱包系统。话不多说&#xff0c;让我们正式…
阅读更多...
python自制PDF转换.PNG格式图片（按每页生成图片完整源码）小工具！

python自制PDF转换.PNG格式图片（按每页生成图片完整源码）小工具！

使用PyQt5应用程序制作PDF转换成图片的小工具&#xff0c;可以导入PDF文档后一键生成对应的PNG图片。 PDF图片转换小工具使用的中间件&#xff1a; python版本&#xff1a;3.6.8 UI应用版本&#xff1a;PyQt5 PDF文件操作非标准库&#xff1a;PyPDF2 PNG图片生成库&#xff1…
阅读更多...
VINS-Mono/Fusion与OpenCV去畸变对比

VINS-Mono/Fusion与OpenCV去畸变对比

VINS中没有直接使用opencv的去畸变函数&#xff0c;而是自己编写了迭代函数完成去畸变操作&#xff0c;主要是为了加快去畸变计算速度 本文对二者的结果精度和耗时进行了对比 VINS-Mono/Fusion与OpenCV去畸变对比1 去畸变原理2 代码实现2.1 OpenCV去畸变2.2 VINS去畸变3 二者对…
阅读更多...
压缩20M文件从30秒到1秒的优化过程

压缩20M文件从30秒到1秒的优化过程

压缩20M文件从30秒到1秒的优化过程 有一个需求需要将前端传过来的10张照片&#xff0c;然后后端进行处理以后压缩成一个压缩包通过网络流传输出去。之前没有接触过用Java压缩文件的&#xff0c;所以就直接上网找了一个例子改了一下用了&#xff0c;改完以后也能使用&#xff0…
阅读更多...
（考研湖科大教书匠计算机网络）第四章网络层-第九节：虚拟专用网与网络地址转换

（考研湖科大教书匠计算机网络）第四章网络层-第九节：虚拟专用网与网络地址转换

获取pdf&#xff1a;密码7281专栏目录首页&#xff1a;【专栏必读】考研湖科大教书匠计算机网络笔记导航 文章目录一&#xff1a;虚拟专用网&#xff08;1&#xff09;虚拟专用网是什么&#xff08;2&#xff09;虚拟专用网如何分配IP地址&#xff08;3&#xff09;例子&#x…
阅读更多...
【JAVA八股文】框架相关

【JAVA八股文】框架相关

框架相关1. Spring refresh 流程2. Spring bean 生命周期3. Spring bean 循环依赖解决 set 循环依赖的原理4. Spring 事务失效5. Spring MVC 执行流程6. Spring 注解7. SpringBoot 自动配置原理8. Spring 中的设计模式1. Spring refresh 流程 Spring refresh 概述 refresh 是…
阅读更多...
深度学习（1）神经网络基础

深度学习（1）神经网络基础

要学习深度学习&#xff0c;那么首先要熟悉神经网络&#xff08;Neural Networks&#xff0c;简称NN&#xff09;的一些基本概念。当然&#xff0c;这里所说的神经网络不是生物学的神经网络&#xff0c;我们将其称之为人工神经网络&#xff08;Artificial Neural Networks&…
阅读更多...
海豚调度2.0.5 星环驱动包踩坑（二）worker服务正常、zk注册正常，心跳时间不更新，也不执行任务，任务一直处于执行中状态

海豚调度2.0.5 星环驱动包踩坑（二）worker服务正常、zk注册正常，心跳时间不更新，也不执行任务，任务一直处于执行中状态

目录背景问题记录20230206 发现服务启动失败20230215 有一台worker不执行作业&#xff0c;其它均正常问题解决问题思考背景 之前分享过海豚调度2.0.5连接星环库使用记录&#xff0c;后来说存储过程又出现了超时的情况&#xff0c;原因是因为调度星环驱动包和生产星环库驱动包不…
阅读更多...
ES 异常写入解决流程

ES 异常写入解决流程

问题说明 一天下午&#xff0c;在北京客户现场的同学反馈我们elasticsearch出现的大量的异常&#xff0c;他反馈说他使用多线程写入大量数据到elasticsearch集群时&#xff0c;隔一段时间之后就会出现CircuitBreakingException&#xff0c;多尝试几次后&#xff0c;他就把问题反…
阅读更多...
基于微信小程序的微信社团小程序

基于微信小程序的微信社团小程序

文末联系获取源码 开发语言&#xff1a;Java 框架&#xff1a;ssm JDK版本&#xff1a;JDK1.8 服务器&#xff1a;tomcat7 数据库&#xff1a;mysql 5.7/8.0 数据库工具&#xff1a;Navicat11 开发软件&#xff1a;eclipse/myeclipse/idea Maven包&#xff1a;Maven3.3.9 浏览器…
阅读更多...
JavaEE|网络原理·上

JavaEE|网络原理·上

文章目录一、网络发展史1.独立模式2.网络互联3.局域网&#xff08;LAN&#xff09;4.广域网&#xff08;WAN&#xff09;局域网组网的方式①基于网线直连②基于集线器&#xff08;hub&#xff09;组建③基于交换机(switch)组建④基于交换机和路由器组建二、网络通信基础1.ip地址…
阅读更多...
Winform控件开发（14）——NotifyIcon（史上最全）

Winform控件开发（14）——NotifyIcon（史上最全）

前言： 先看个气泡提示框的效果： 代码如下： 在一个button中注册click事件，当我们点击button1时，就能显示气泡 private void button1_Click(object sender, EventArgs e){notifyIcon1.Visible = true;notifyIcon1
阅读更多...
【论文速递】ICLR2018 - 用于小样本语义分割的条件网络

【论文速递】ICLR2018 - 用于小样本语义分割的条件网络

【论文速递】ICLR2018 - 用于小样本语义分割的条件网络 【论文原文】&#xff1a;CONDITIONAL NETWORKS FOR FEW-SHOT SEMANTIC SEGMENTATION&#xff08;Workshop track - ICLR 2018&#xff09; 【作者信息】&#xff1a;Kate Rakelly Evan Shelhamer Trevor Darrell Alexe…
阅读更多...
PyTorch - Conv2d 和 MaxPool2d

PyTorch - Conv2d 和 MaxPool2d

文章目录Conv2d计算Conv2d 函数解析代码示例MaxPool2d计算函数说明卷积过程动画Transposed convolution animationsTransposed convolution animations参考视频&#xff1a;土堆说 卷积计算 https://www.bilibili.com/video/BV1hE411t7RN 关于 torch.nn 和 torch.nn.function t…
阅读更多...
Reverse入门[不断记录]

Reverse入门[不断记录]

文章目录前言一、[SWPUCTF 2021 新生赛]re1二、[SWPUCTF 2021 新生赛]re2三、[GFCTF 2021]wordy[花指令]四、[NSSRound#3 Team]jump_by_jump[花指令]五、[NSSRound#3 Team]jump_by_jump_revenge[花指令]前言 心血来潮&#xff0c;想接触点Reverse&#xff0c;感受下Reverse&am…
阅读更多...
网络编程(一)

网络编程(一)

网络编程 文章目录网络编程前置概念1- 字节序高低地址与高低字节高低地址&#xff1a;高低字节字节序大端小端例子代码判断当前机器是大端还是小端为何要有字节序字节序转换函数需要字节序转换的时机例子一例子二2- IP地址转换函数早期(不用管)举例现在与字节序转换函数相比:**…
阅读更多...
模块化热更思路

模块化热更思路

title: 模块化热更思路 categories: Others tags: [热更, 模块化, 分包] date: 2023-02-18 01:04:57 comments: false mathjax: true toc: true 模块化热更 浅浅的记录一下访问破 200w (But, I don’t care about this.) 前篇 只谈思路, 不贴实现代码. 需求 游戏类型属于合集…
阅读更多...
Linux（十三）设计模式——单例模式

Linux（十三）设计模式——单例模式

设计模式——针对典型场景所设计出来的特别的处理方案 单例模式&#xff1a;一个类只能实例化一个对象&#xff08;所以叫单例&#xff09; 场景&#xff1a; 1、资源角度&#xff1a;资源在内存中只占有一份 2、数据角度&#xff1a;如果只有一个对象&#xff0c;那么该对象在…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023