深度学习（1）神经网络基础

要学习深度学习，那么首先要熟悉神经网络（Neural Networks，简称NN）的一些基本概念。

当然，这里所说的神经网络不是生物学的神经网络，我们将其称之为人工神经网络（Artificial Neural Networks，简称ANN）貌似更为合理。神经网络最早是人工智能领域的一种算法或者说是模型，目前神经网络已经发展成为一类多学科交叉的学科领域，它也随着深度学习取得的进展重新受到重视和推崇。

为什么说是“重新”呢？其实，神经网络最为一种算法模型很早就已经开始研究了，但是在取得一些进展后，神经网络的研究陷入了一段很长时间的低潮期，后来随着Hinton在深度学习上取得的进展，神经网络又再次受到人们的重视。

神经元模型

神经元是神经网络中最基本的结构，也可以说是神经网络的基本单元，它的设计灵感完全来源于生物学上神经元的信息传播机制。

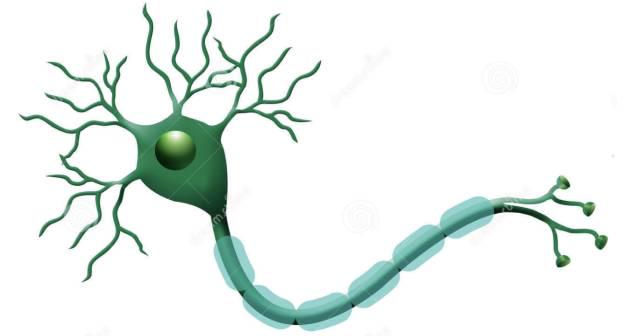
1943年，McCulloch和Pitts将上图的神经元结构用一种简单的模型进行了表示，构成了一种人工神经元模型，也就是我们现在经常用到的“M-P神经元模型”，如下图所示：

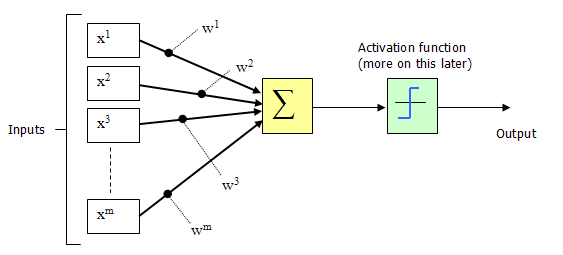
从上图M-P神经元模型可以看出，神经元的输出

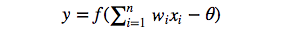
其中

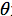
为我们之前提到的神经元的激活阈值，函数

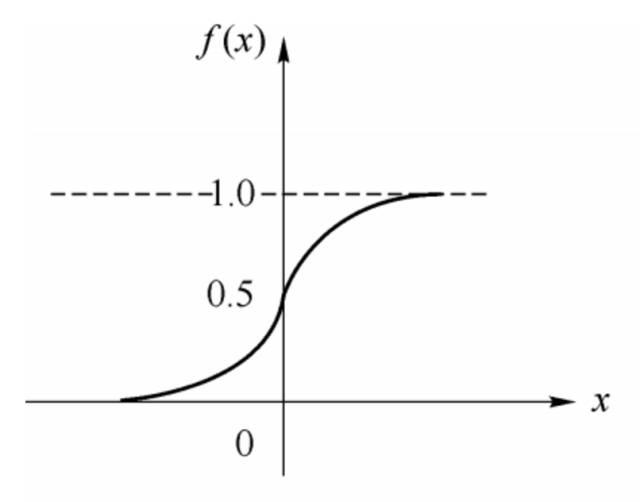
也被称为是激活函数。如上图所示，函数

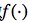
可以用一个阶跃方程表示，大于阈值激活；否则则抑制。

但是这样有点太粗暴，因为阶跃函数不光滑，不连续，不可导，因此我们更常用的方法是用sigmoid函数来表示函数

。

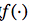
sigmoid函数的表达式和分布图如下所示：

感知机和神经网络

感知机（perceptron）是由两层神经元组成的结构，输入层用于接受外界输入信号，输出层（也被称为是感知机的功能层）就是M-P神经元。

下图表示了一个输入层具有三个神经元（分别表示为

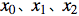
）的感知机结构：

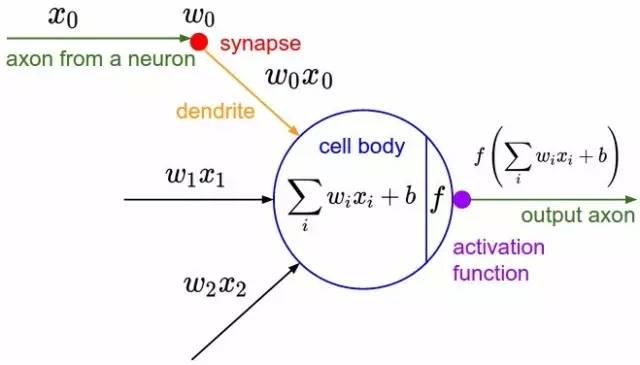
根据上图不难理解，感知机模型可以由如下公式表示：

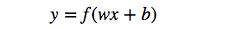
其中，

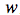
为感知机输入层到输出层连接的权重，

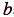
表示输出层的偏置。

事实上，感知机是一种判别式的线性分类模型，可以解决与、或、非这样的简单的线性可分（linearly separable）问题，线性可分问题的示意图见下图：

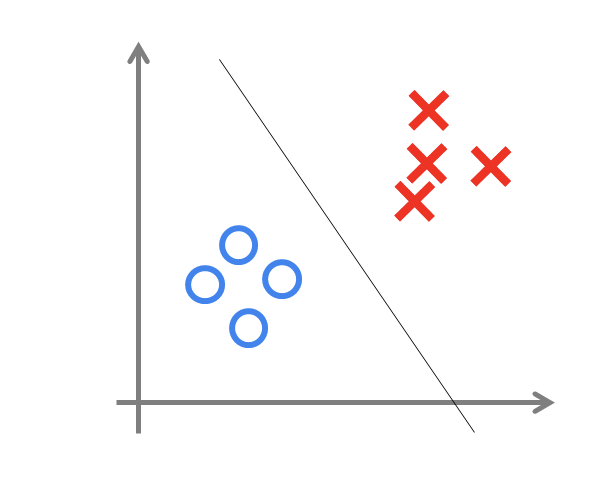
但是由于它只有一层功能神经元，所以学习能力非常有限。事实证明，单层感知机无法解决最简单的非线性可分问题——异或问题（有想了解异或问题或者是感知机无法解决异或问题证明的同学请移步这里《证：单层感知机不能表示异或逻辑》）。

关于感知机解决异或问题还有一段历史值得我们简单去了解一下：感知器只能做简单的线性分类任务。但是当时的人们热情太过于高涨，并没有人清醒的认识到这点。于是，当人工智能领域的巨擘Minsky指出这点时，事态就发生了变化。Minsky在1969年出版了一本叫《Perceptron》的书，里面用详细的数学证明了感知器的弱点，尤其是感知器对XOR（异或）这样的简单分类任务都无法解决。Minsky认为，如果将计算层增加到两层，计算量则过大，而且没有有效的学习算法。

所以，他认为研究更深层的网络是没有价值的。由于Minsky的巨大影响力以及书中呈现的悲观态度，让很多学者和实验室纷纷放弃了神经网络的研究。神经网络的研究陷入了冰河期。这个时期又被称为“AI winter”。接近10年以后，对于两层神经网络的研究才带来神经网络的复苏。

我们知道，我们日常生活中很多问题，甚至说大多数问题都不是线性可分问题，那我们要解决非线性可分问题该怎样处理呢？这就是这部分我们要引出的“多层”的概念。

既然单层感知机解决不了非线性问题，那我们就采用多层感知机，下图就是一个两层感知机解决异或问题的示意图：

构建好上述网络以后，通过训练得到最后的分类面如下：

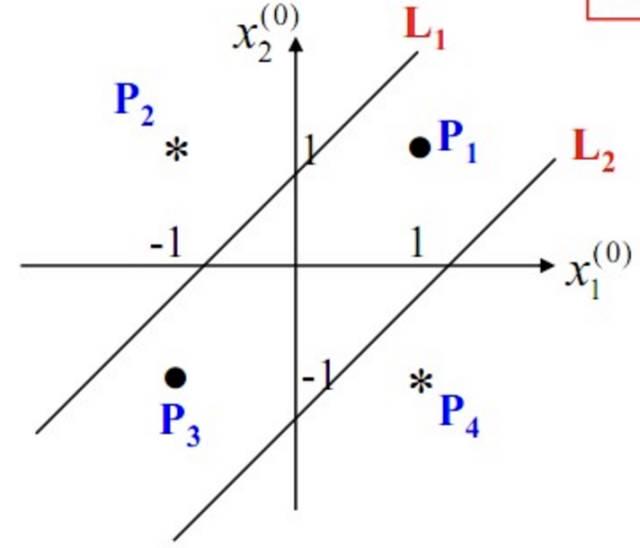
由此可见，多层感知机可以很好的解决非线性可分问题，我们通常将多层感知机这样的多层结构称之为是神经网络。

但是，正如Minsky之前所担心的，多层感知机虽然可以在理论上可以解决非线性问题，但是实际生活中问题的复杂性要远不止异或问题这么简单，所以我们往往要构建多层网络，而对于多层神经网络采用什么样的学习算法又是一项巨大的挑战，如下图所示的具有4层隐含层的网络结构中至少有33个参数（不计偏置bias参数），我们应该如何去确定呢？

误差逆传播算法

所谓神经网络的训练或者是学习，其主要目的在于通过学习算法得到神经网络解决指定问题所需的参数，这里的参数包括各层神经元之间的连接权重以及偏置等。

因为作为算法的设计者（我们），我们通常是根据实际问题来构造出网络结构，参数的确定则需要神经网络通过训练样本和学习算法来迭代找到最优参数组。

说起神经网络的学习算法，不得不提其中最杰出、最成功的代表——误差逆传播（error BackPropagation，简称BP）算法。BP学习算法通常用在最为广泛使用的多层前馈神经网络中。

BP算法的主要流程可以总结如下：

输入：训练集

学习率;

过程：

1. 在（0，1）范围内随机初始化网络中所有连接权和阈值

2. repeat:

3.　　 for all

4. 　　　　根据当前参数计算当前样本的输出;

5. 　　　　计算输出层神经元的梯度项；

6. 　　　　计算隐层神经元的梯度项；

7. 　　　　更新连接权与阈值

8. 　　end for

9. until 达到停止条件

输出：连接权与阈值确定的多层前馈神经网络

实例

4.1 问题与数据

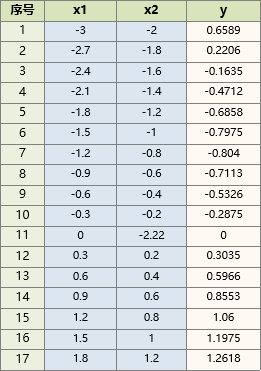
数据如下，x1,x2为输入，y为对应的输出，现需要训练一个网络，用x1,x2预测y.

4.2 确定模型结构与训练算法

我们这里采用的网络结构如下：

1：节点个数设置：输入层、隐层、输出层的节点个数分别为[2 ，3，1]。

2：传递函数设置：隐层（ tansig函数）。输出层（purelin函数）。

3：训练方式：trainlm。

则模型结构拓扑图如下：

模型的数学表达式如下：

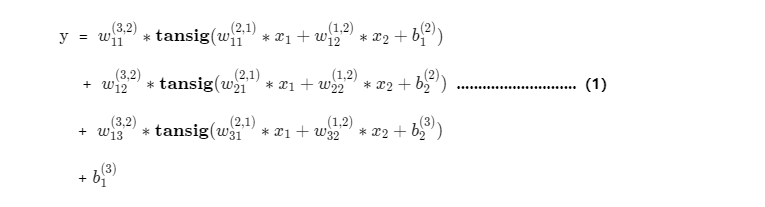
4.3代码实现

在matlab2014b里写代码：

x1 = [-3,-2.7,-2.4,-2.1,-1.8,-1.5,-1.2,-0.9,-0.6,-0.3,0,0.3,0.6,0.9,1.2,1.5,1.8];% x1：x1 = -3:0.3:2;
x2 = [-2,-1.8,-1.6,-1.4,-1.2,-1,-0.8,-0.6,-0.4,-0.2,-2.2204,0.2,0.4,0.6,0.8,1,1.2]; % x2：x2 = -2:0.2:1.2;
y  = [0.6589,0.2206,-0.1635,-0.4712,-0.6858,-0.7975,-0.8040,...
          -0.7113,-0.5326,-0.2875 ,0,0.3035,0.5966,0.8553,1.0600,1.1975,1.2618];    % y： y = sin(x1)+0.2*x2.*x2;
 
inputData  = [x1;x2];      % 将x1,x2作为输入数据
outputData = y;            % 将y作为输出数据
setdemorandstream(88888);%指定随机种子，这样每次训练出来的网络都一样。
 
%使用用输入输出数据（inputData、outputData）建立网络，
%隐节点个数设为3.其中隐层、输出层的传递函数分别为tansig和purelin，使用trainlm方法训练。
 
net = newff(inputData,outputData,3,{'tansig','purelin'},'trainlm');
 
%设置一些常用参数
net.trainparam.goal = 0.0001;               % 训练目标：均方误差低于0.0001
net.trainparam.show = 400;                  % 每训练400次展示一次结果
net.trainparam.epochs = 15000;              % 最大训练次数：15000.
[net,tr] = train(net,inputData,outputData); % 调用matlab神经网络工具箱自带的train函数训练网络
 
 
simout = sim(net,inputData);                % 调用matlab神经网络工具箱自带的sim函数得到网络的预测值
figure;                                     % 新建画图窗口窗口
t=1:length(simout);
plot(t,y,t,simout,'r')                      % 画图，对比原来的y和网络预测的y

运行后得到训练的图：

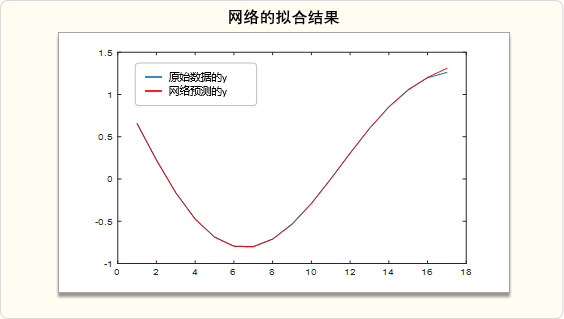
4.4 网络预测

若果想知道x1=0.5,x2=0.5时的值，可输入

x    =[0.5;0.5];simy = sim(net,x)

命令窗口输出：

这样，就得到了输入为 [0.5,0.5] 时，y的预测值。

4.5 获取最终数学表达式

实际上训练好的网络net, 就是上面的（1）式的数学函数，

预测的时候可以直接使用神经网络工具箱的 sim(net,x) 函数进行预测，

但如果一定要把这个数学表达式提取出来呢？

以下两张文章都有所介绍：

(1)《提取神经网络数学表达式》

(2)《一个BP的完整代码实现》

参考文献

一个简单的神经网络例子 https://blog.csdn.net/dbat2015/article/details/48463047

干货|最详尽的神经网络基础 https://mp.weixin.qq.com/s?__biz=MzI4MDYzNzg4Mw==&mid=2247484133&idx=1&sn=92291cebd4b5eeddddab975d90dfc312&chksm=ebb43a31dcc3b3271684a1390efeb849a6b32bfa7038ec6b1c42486a1c22ac0f9083720d4730&scene=27