电子技术——CS和CE放大器的高频响应

在绘制出MOS和BJT的高频响应模型之后,我们对MOS和BJT的高频响应有了进一步的认识。现在我们想知道的是在高频响应中 f H f_H fH 的关系。
高频响应分析对电容耦合还是直接耦合都是适用的,因为在电容耦合中高频模式下此时电容可以看做是完美短路。
CS放大器
下图是一个CS放大器的高频模型:
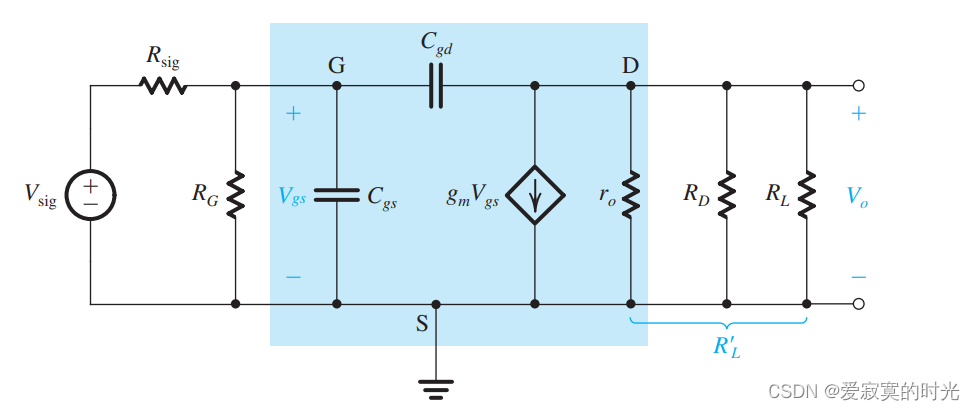
其中输入端和输出端可以使用戴维南等效定理替代:
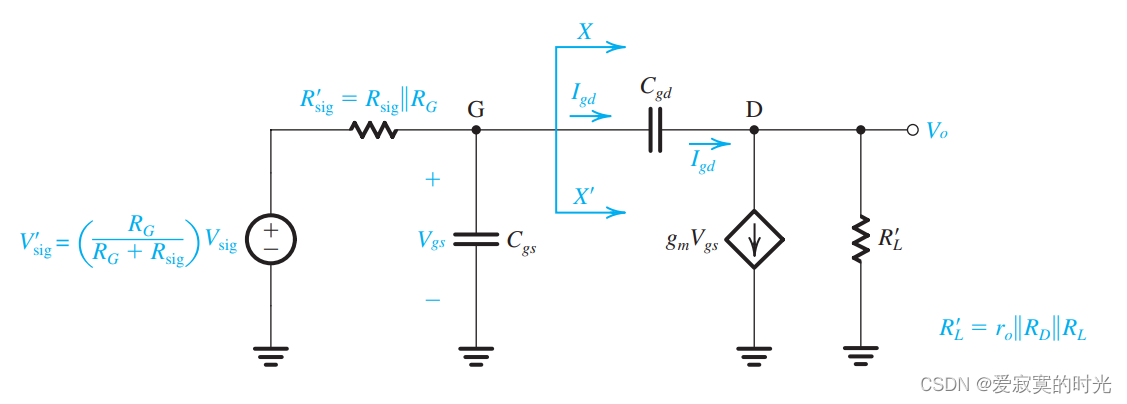
上图中,当
C
g
s
C_{gs}
Cgs 和
C
g
d
C_{gd}
Cgd 均为零的时候,此时获得最大增益
∣
A
M
∣
|A_M|
∣AM∣ :
A M = − R G R G + R s i g ( g m R L ′ ) A_M = -\frac{R_G}{R_G + R_{sig}}(g_m R_L') AM=−RG+RsigRG(gmRL′)
通过上述的等效电路,我们当然可以写出一个关于复频率 s s s 的传递方程 V o / V s i g V_o / V_{sig} Vo/Vsig 。因为图中存在两个电容的,则传递方程一定是一个二阶多项式方程。之后便可以确定零点和极点。但是,这个方法还是比较困难的,而且无法给我们一个有效的方式快速确实什么才是高频响应的决定因素。为此我们需要一个更加绝妙的方法。所以我们不打算计算传递方程,而是使用估算的方法快速确定高频响应的决定因素。
我们的思路在输入端简化电路,然后使用简单的RC低通网络解决。所以,我们要去掉电容 C g d C_{gd} Cgd ,寻找一个等价的 C e q C_{eq} Ceq 代替。
首先我们考虑放大器的输出端,其电压为:
V o = − ( g m V g s ) R L ′ + I g d R L ′ V_o = -(g_m V_{gs})R_L' + I_{gd}R_L' Vo=−(gmVgs)RL′+IgdRL′
因为 g m V g s ≫ I g d g_m V_{gs} \gg I_{gd} gmVgs≫Igd 所以:
V o ≃ − ( g m V g s ) R L ′ V_o \simeq -(g_m V_{gs})R_L' Vo≃−(gmVgs)RL′
再观察电流 I g d I_{gd} Igd :
I g d = s C g d ( V g s − V o ) = s C g d [ V g s − ( − g m R L ′ V g s ) ] = s C g d ( 1 + g m R L ′ ) V g s I_{gd} = sC_{gd}(V_{gs} - V_o) = sC_{gd}[V_{gs} - (-g_mR_L'V_{gs})] = sC_{gd}(1 + g_mR_L')V_{gs} Igd=sCgd(Vgs−Vo)=sCgd[Vgs−(−gmRL′Vgs)]=sCgd(1+gmRL′)Vgs
现在,我们从 X X ′ XX' XX′ 方向向右看去,流过的电流是 I g d I_{gd} Igd 因此,我们只需要使用一个从栅极到地的等效电容 G e q G_{eq} Geq 并且使得其流过的电流仍然为 I g d I_{gd} Igd 即可。
s C e q V g s = s C g d ( 1 + g m R L ′ ) V g s sC_{eq}V_{gs} = sC_{gd}(1 + g_mR_L')V_{gs} sCeqVgs=sCgd(1+gmRL′)Vgs
因此:
C e q = C g d ( 1 + g m R L ′ ) C_{eq} = C_{gd}(1 + g_mR_L') Ceq=Cgd(1+gmRL′)
现在 C g d C_{gd} Cgd 变成了较大的输入端电容 C e q C_{eq} Ceq 。如图:
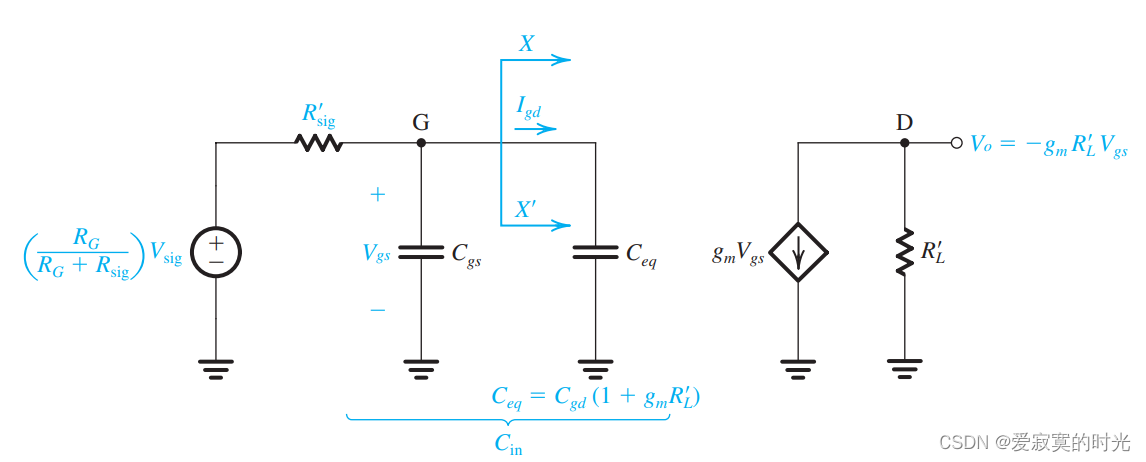
乘以因子
(
1
+
g
m
R
L
′
)
(1 + g_mR_L')
(1+gmRL′) 是因为
C
g
d
C_{gd}
Cgd 连接在G与D直接,并且之间存在一个电压增益
g
m
R
L
′
g_mR_L'
gmRL′ 。这个效应称为 米勒效应 。因子
(
1
+
g
m
R
L
′
)
(1 + g_mR_L')
(1+gmRL′) 称为 米勒因子 。
现在输入端变成了一个简单的RC低通型STC网络:
V g s = ( R G R G + R s i g V s i g ) 1 1 + s ω 0 V_{gs} = (\frac{R_G}{R_G + R_{sig}}V_{sig})\frac{1}{1 + \frac{s}{\omega_0}} Vgs=(RG+RsigRGVsig)1+ω0s1
这里 ω 0 \omega_0 ω0 是极点频率:
ω 0 = 1 / C i n R s i g ′ \omega_0 = 1/C_{in}R_{sig}' ω0=1/CinRsig′
这里 C i n C_{in} Cin 为:
C i n = C g s + C e q C_{in} = C_{gs} + C_{eq} Cin=Cgs+Ceq
最后我们就可以得到:
V o V s i g = − ( R G R G + R s i g ) ( g m R L ′ ) ( 1 1 + s ω 0 ) \frac{V_o}{V_{sig}} = -(\frac{R_G}{R_G + R_{sig}})(g_m R_L')(\frac{1}{1 + \frac{s}{\omega_0}}) VsigVo=−(RG+RsigRG)(gmRL′)(1+ω0s1)
也就是:
V o V s i g = A M 1 + s ω H \frac{V_o}{V_{sig}} = \frac{A_M}{1 + \frac{s}{\omega_H}} VsigVo=1+ωHsAM
这里:
ω H = ω 0 = 1 C i n R s i g ′ \omega_H = \omega_0 = \frac{1}{C_{in}R_{sig}'} ωH=ω0=CinRsig′1
f H = 1 2 π C i n R s i g ′ f_H = \frac{1}{2\pi C_{in}R_{sig}'} fH=2πCinRsig′1
最后我们发现CS放大器的高频响应可以等效为一个低通型RC网络的高频响应:
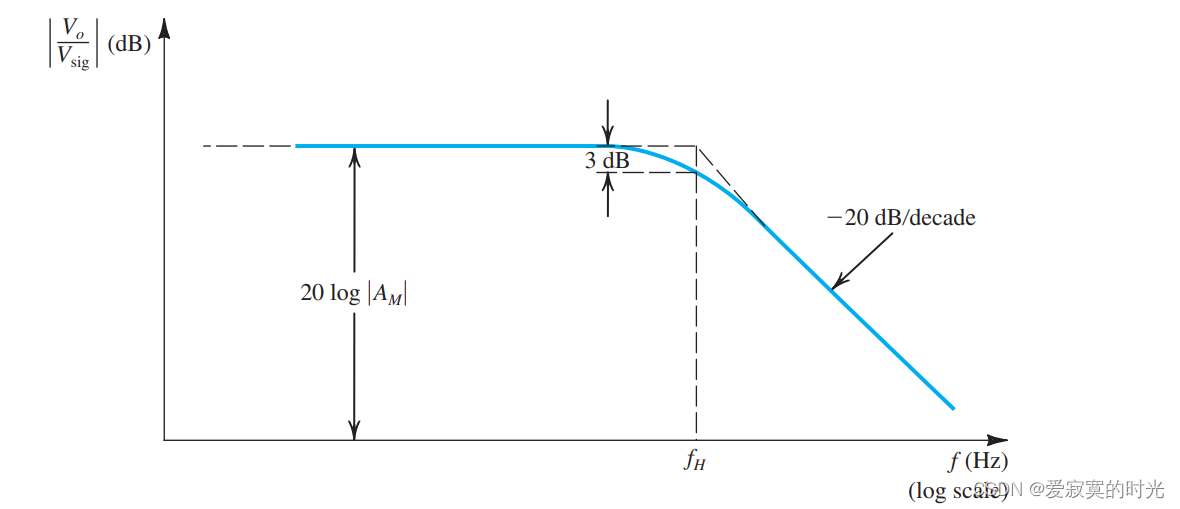
总结如下:
- 我们发现 f H f_H fH 反比于 R s i g ′ ≃ R s i g R_{sig}' \simeq R_{sig} Rsig′≃Rsig 这说明信号源内阻越大, f H f_H fH 越小。
- 我们发现尽管 C g d C_{gd} Cgd 比较小,但是乘完因子之后 C e q C_{eq} Ceq 却很大,所以 C e q C_{eq} Ceq 称为了贡献 C i n C_{in} Cin 的主要因素,所以越大的 C e q C_{eq} Ceq 则会造成 f H f_H fH 越小。
- 这给我们一个扩宽放大器带宽的一个思路,就是尽量降低米勒效应。
- 上述分析都是一种估计分析,也就是说 I g d I_{gd} Igd 必须非常小,并且频率也不能超过 f H f_H fH 太多。一个精准的分析应该是具有两个极点,其极点频率远大于 f H f_H fH 并且有两个传输零点分别是 s = ∞ s = \infty s=∞ 和 s = g m / C g d s = g_m / C_{gd} s=gm/Cgd 都是远大于 f H f_H fH 的,因此在只估计 f H f_H fH 的时候,以上因素均可以忽略。同时,这个方法指出影响放大器高频响应的关键因素:米勒效应。
- CS放大器在高频具有主导频率 f P ≃ f H f_P \simeq f_H fP≃fH 。
CE放大器
下图展示了CE放大器的高频等效模型:
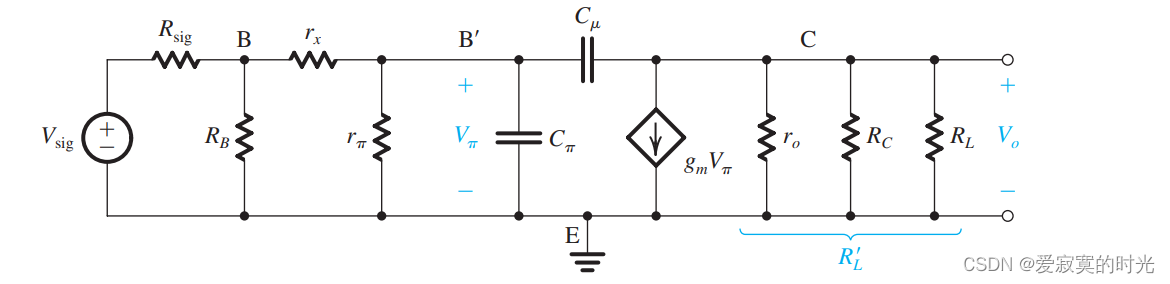
同样的我们进行戴维南等效:
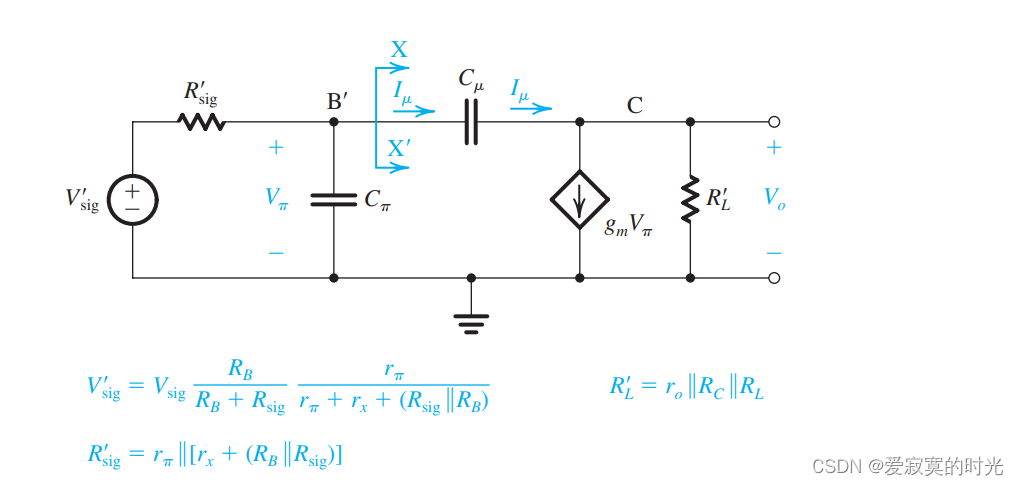
则此时原始的电压增益为:
A M = V o V s i g = − R B R B + R s i g r π r π + r x + ( R s i g ∣ ∣ R B ) ( g m R L ′ ) A_M = \frac{V_o}{V_{sig}} = -\frac{R_B}{R_B + R_{sig}}\frac{r_\pi}{r_\pi + r_x + (R_{sig} || R_B)}(g_m R_L') AM=VsigVo=−RB+RsigRBrπ+rx+(Rsig∣∣RB)rπ(gmRL′)
我们发现上面的电路图和MOS情况的完全一致,因此可以得到:
V o V s i g = A M 1 + s ω H \frac{V_o}{V_{sig}} = \frac{A_M}{1 + \frac{s}{\omega_H}} VsigVo=1+ωHsAM
这里:
f H = 1 2 π C i n R s i g ′ f_H = \frac{1}{2 \pi C_{in} R_{sig}'} fH=2πCinRsig′1
如图:
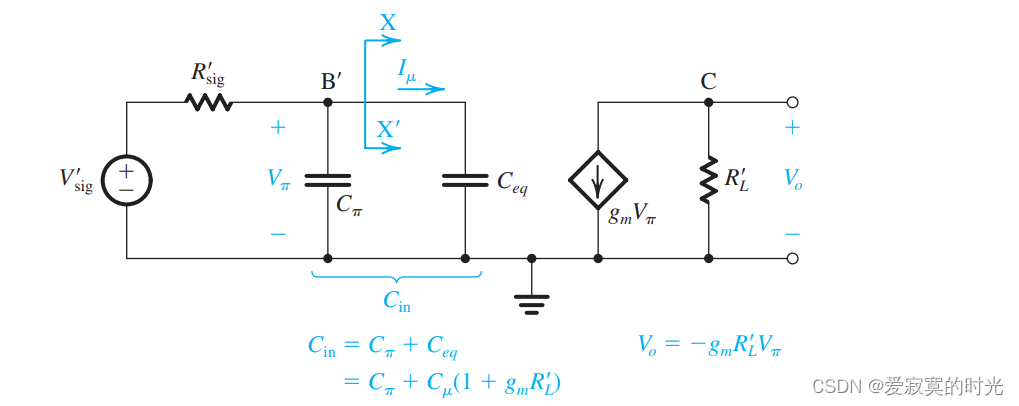
高频响应为:
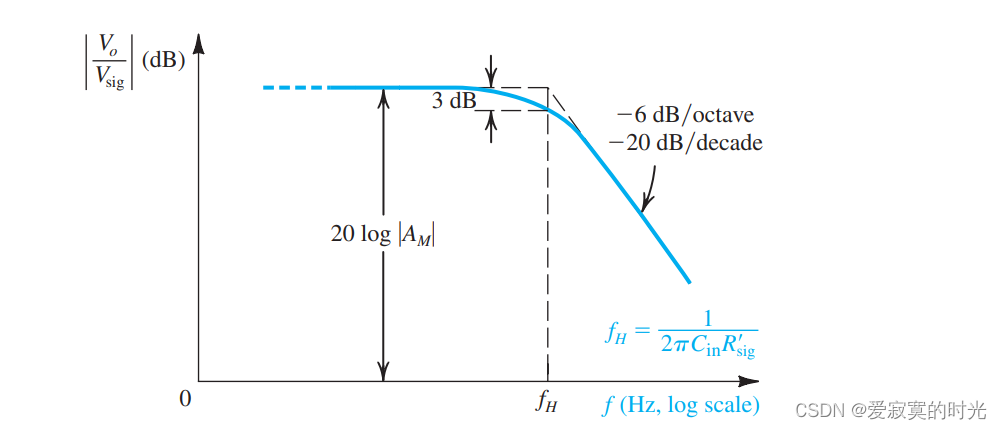
结论和MOS完全相似。
米勒定理
在我们上述的分析中,我们使用等效的 C e q C_{eq} Ceq 代替了桥电容 C g s C_{gs} Cgs 或是 C μ C_\mu Cμ 。这是一个非常快速且有效的方法,我们称为 米勒定理 。
考虑下面的情况:
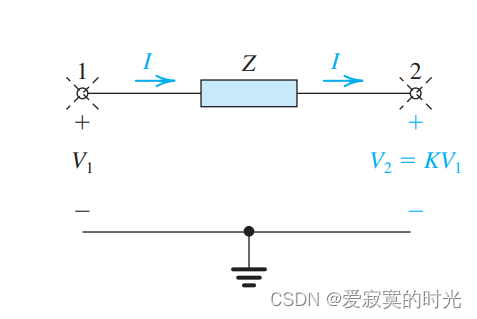
这是一个简化的二端传输网络,端口1和2为电气连接点,中间的阻抗为
Z
Z
Z 。并且我们假设存在电压关系:
V 2 = K V 1 V_2 = KV_1 V2=KV1
米勒定理阐述阻抗 Z Z Z 能够被等效替代成两个对地阻抗 Z 1 Z_1 Z1 和 Z 2 Z_2 Z2 ,称为米勒等效电路,如图:
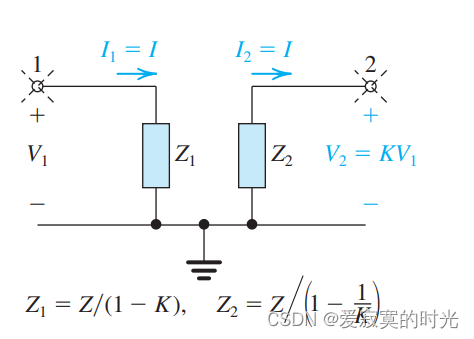
其中:
Z 1 = Z / ( 1 − K ) Z_1 = Z/(1 - K) Z1=Z/(1−K)
Z 2 = Z / ( 1 − 1 K ) Z_2 = Z / (1 - \frac{1}{K}) Z2=Z/(1−K1)
若要证明这个定理,我们必须保证电流关系不变,对于端口1来说:
I 1 = V 1 Z 1 = I = V 1 − K V 1 Z I_1 = \frac{V_1}{Z_1} = I = \frac{V_1 - KV_1}{Z} I1=Z1V1=I=ZV1−KV1
同样的对于端口2:
I 2 = 0 − V 2 Z 2 = 0 − K V 1 Z 2 = I = V 1 − K V 1 Z I_2 = \frac{0 - V_2}{Z_2} = \frac{0 - KV_1}{Z_2} = I = \frac{V_1 - KV_1}{Z} I2=Z20−V2=Z20−KV1=I=ZV1−KV1
我们发现,使用米勒等效替代之后,我们在输入端获得了一个和 1 − K 1-K 1−K 有关的一个负反馈电阻,负反馈因子 1 − K 1-K 1−K 我们称为 米勒因子 。
最后一点,我们在上面分析CS和CE的过程中,我们忽略了等效的输出电容,因为它实在是太小了 ≃ C g d \simeq C_{gd} ≃Cgd 。
CS放大器在低 R s i g R_{sig} Rsig 时候的的频率响应
有时候,CS放大器的信号源的内阻可能很小,此时的 f H f_H fH 的最大值限制不再受信号源的内阻的影响,如图:
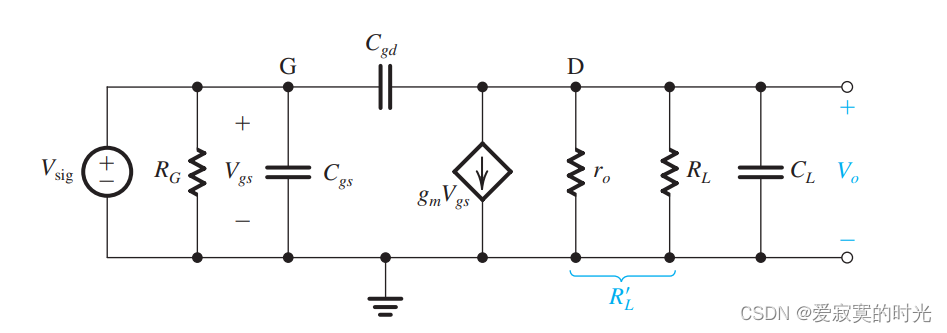
上图中信号源的内阻为零,而且我们在输出端引入了负载电容
C
L
C_L
CL ,负载电容可能由负载自身的容性阻抗或是MOS的
C
d
b
C_{db}
Cdb 或是线间电容等等。之前,我们忽略了
C
L
C_L
CL 是因为
f
H
f_H
fH 的最大值主要受
R
s
i
g
R_{sig}
Rsig 影响。
注意到:
V g s = V s i g V_{gs} = V_{sig} Vgs=Vsig
I g d = s C g d ( V g s − V o ) I_{gd} = sC_{gd}(V_{gs} - V_o) Igd=sCgd(Vgs−Vo)
根据输出节点的电流方程:
I g d = g m V g s + V o R L ′ + s C L V o I_{gd} = g_mV_{gs} + \frac{V_o}{R_L'}+sC_LV_o Igd=gmVgs+RL′Vo+sCLVo
联立方程得到:
V o V s i g = − g m R L ′ 1 − s ( C g d / g m ) 1 + s ( C L + C g d R L ′ ) \frac{V_o}{V_{sig}} = -g_mR_L' \frac{1 - s(C_{gd}/g_m)}{1 + s(C_L + C_{gd}R_L')} VsigVo=−gmRL′1+s(CL+CgdRL′)1−s(Cgd/gm)
我们发现其存在一个零点频率:
f Z = g m 2 π C g d f_Z = \frac{g_m}{2 \pi C_{gd}} fZ=2πCgdgm
极点频率:
f H = 1 2 π ( C L + C g d ) R L ′ f_H = \frac{1}{2 \pi (C_L + C_{gd})R_L'} fH=2π(CL+Cgd)RL′1
为了说明极点是怎么形成的,我们可以观察下图,下图中,我们将电压源置零。
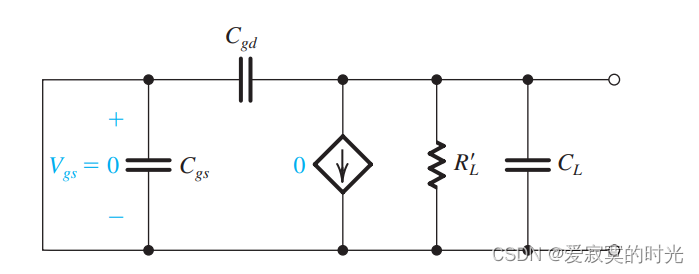
此时 R L ′ R_L' RL′ 可以观察到的电容为 C L + C g d C_L + C_{gd} CL+Cgd 。
我们发现传输零点频率要比 f H f_H fH 大很多:
f Z f H = ( g m R L ′ ) ( 1 + C L C g d ) \frac{f_Z}{f_H} = (g_m R_L')(1 + \frac{C_L}{C_{gd}}) fHfZ=(gmRL′)(1+CgdCL)
因此传输零点一般不影响高频响应。实际上,我们知道,大约从 f H f_H fH 开始,增益 ∣ A M ∣ |A_M| ∣AM∣ 将以 -6dB每八度或-20dB每十倍的速度下降,存在一个假设的理想零点(单位增益) f t f_t ft ,如图:
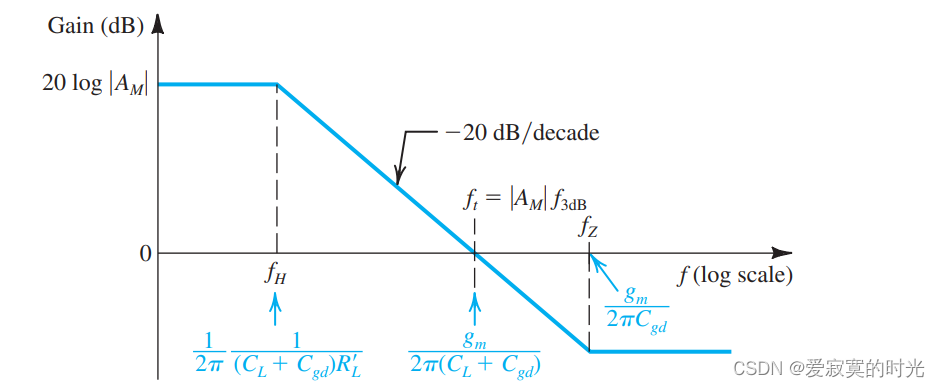
我们可以计算出:
f t = ∣ A M ∣ f H f_t = |A_M|f_H ft=∣AM∣fH
其值等于 增益-带宽积 。
进而:
f t = g m R L ′ 1 2 π ( C L + C g d ) R L ′ = g m 2 π ( C L + C g d ) f_t = g_mR_L'\frac{1}{2 \pi (C_L + C_{gd})R_L'} = \frac{g_m}{2 \pi (C_L + C_{gd})} ft=gmRL′2π(CL+Cgd)RL′1=2π(CL+Cgd)gm
这说明,当频率超过 f t f_t ft 其增益衰减到几乎为0dB。


![[LeetCode]1237. 找出给定方程的正整数解](https://img-blog.csdnimg.cn/3a3c37b60d8a4b82bf6d8e537608bc38.png)
![[Android Studio] Android Studio Virtual Device(AVD)虚拟机的功能试用](https://img-blog.csdnimg.cn/24b696d76d374a9992017e1625389592.gif)