题目链接：https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/
题目描述：

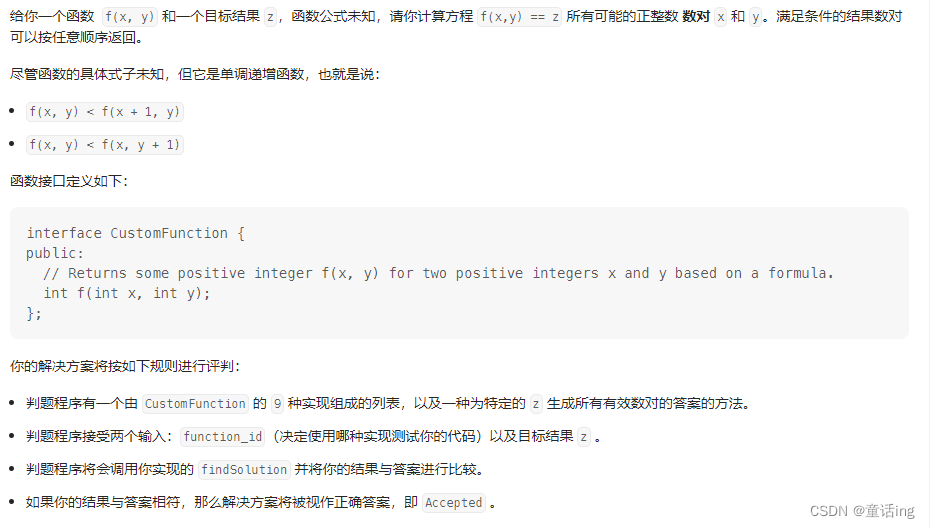
样例1：

输入：function_id = 1, z = 5
输出：[[1,4],[2,3],[3,2],[4,1]]
解释：function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5：
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5

样例2：

输入：function_id = 2, z = 5
输出：[[1,5],[5,1]]
解释：function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5：
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5

题目限定：

方法1：暴力枚举

func findSolution(customFunction func(int, int) int, z int) [][]int {
    res := make([][]int, 0, 100)
    for x := 1; x <= 1000; x++ {
        for y := 1; y<= 1000; y++ {
            if customFunction(x,y) == z {
                temp := []int{x, y}
                res = append(res,temp)
            }
        }
    }
    return res
}

暴力枚举法每次都从开始找y，x最多枚举1000次，而y每次也会枚举1000次，因此，总的复杂度为O(x*y)。

方法2：枚举+二分查找

func findSolution(customFunction func(int, int) int, z int) (res [][]int)  {
    for x := 1; x <= 1000; x++ {
        l, r := 1, 1000
        for l <= r {
            mid := (l+r)/2
            if customFunction(x,mid) == z {
                res = append(res, []int{x,mid})
                break
            } else if customFunction(x,mid) > z {
                r = mid -1 
            } else {
                l = mid + 1
            }
        }
    }
    return res
}

既然我们知道y每次都从头开始找比较慢，那么我们可以优化y的查找时间，利用二分查找即可将找y的复杂度降到log级别，因此总的时间复杂度为O(xlogy)。

当然，golang中也可以使用sort库的Search方法：

func findSolution(customFunction func(int, int) int, z int) (res [][]int) {
	for x := 1; x <= 1000; x++ {
		y := 1 + sort.Search(999, func(y int) bool {
			return customFunction(x, y+1) >= z
		})
		if customFunction(x,y) == z {
			res = append(res, []int{x,y})
		}
	}
	return res
}

同时需要注意Search的用法，是从[0,n)去查找的，所以类似我们是从0-999中查找出来的下标，最后加上1就表示从1到1000了：

// Search uses binary search to find and return the smallest index i
// in [0, n) at which f(i) is true, assuming that on the range [0, n),
// f(i) == true implies f(i+1) == true. That is, Search requires that
// f is false for some (possibly empty) prefix of the input range [0, n)
// and then true for the (possibly empty) remainder; Search returns
// the first true index. If there is no such index, Search returns n.
// (Note that the “not found” return value is not -1 as in, for instance,
方法3：双指针

func findSolution(customFunction func(int, int) int, z int) (res [][]int)  {
    y := 1000
    for x := 1; x <= 1000; x++ {
        for ; y > 0 ; y-- {
            if customFunction(x,y) < z {
                break
            }
            if customFunction(x,y) == z {
                res = append(res, []int{x,y})
                break
            }
        }
    }
    return res
}

这种方法关键在于直接利用函数单调递增的特性，一个答案从前往后找，另一个答案从后往前找，下一次寻找一定是基于上一次的结果，因此会少很多次遍历，x最多遍历1000次，y总的遍历次数也最多1000次，因此总的时间复杂度为O(x+y)。