QM9数据集示例项目学习图神经网络

news2024/11/16 9:52:48

QM9数据集：

QM9为小有机分子的相关的、一致的和详尽的化学空间提供量子化学特征，该数据库可用于现有方法的基准测试，新方法的开发，如混合量子力学/机器学习，以及结构-性质关系的系统识别。

新药物和新材料的计算从头设计需要对化合物空间进行严格和公正的探索。然而，由于其大小与分子大小相结合，大量未知领域仍然存在。报告计算了由CHONF组成的134k稳定有机小分子的几何、能量、电子和热力学性质。这些分子对应于GDB-17化学宇宙中1660亿个有机分子中所有133,885个含有多达9个重原子(CONF)的物种的子集。报告了能量最小的几何，相应的谐波频率，偶极矩，极化率，以及能量，焓，和原子化的自由能。所有性质都是在量子化学的B3LYP/6-31G(2df,p)水平上计算的。此外，对于主要的化学计量，C7H10O2，在134k分子中有6095个组成异构体。在更精确的G4MP2理论水平上报告了所有这些原子化的能量、焓和自由能。因此，该数据集为相关、一致和全面的小有机分子化学空间提供了量子化学性质。该数据库可用于现有方法的基准测试，新方法的开发，如混合量子力学/机器学习，以及结构-性质关系的系统识别。

一些有机分子如下：

在这里插入图片描述

数据集中的分子可视化：

在这里插入图片描述
文件XYZ格式：

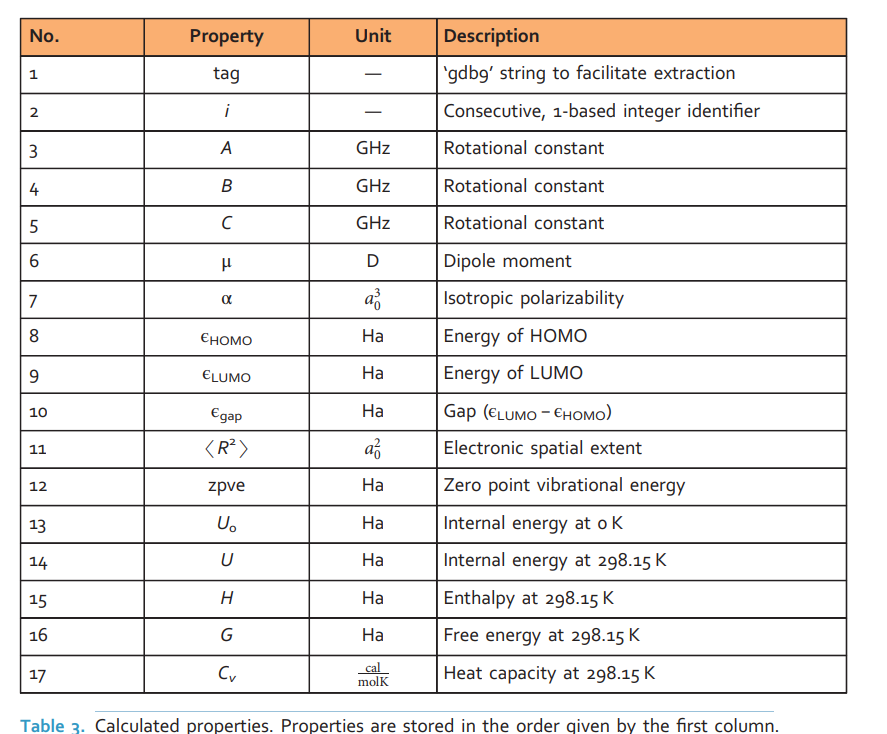
对于每个分子，原子坐标和计算属性存储在名为dataset_index.xyz的文件中。XYZ格式(最初由明尼苏达超级计算机中心为XMol程序开发)是一种广泛使用的纯文本格式，用于编码分子的笛卡尔坐标，没有正式的规范。它包含一个标题行(na)、一个注释行和na行(na行包含元素类型和原子坐标)，每行一个原子。我们扩展了这种格式，如表2所示。现在，注释行用于存储所有标量属性

QM9数据提取的特征：

能量最小的几何空间结构、相应的谐波频率、偶极矩、极化率、能量、焓、原子化的自由能等

在这里插入图片描述

网络结构的设计

Set2Set的聚合方式：

Set2Set指的是一种序列到序列的一种扩展。许多情况下，可变大小的输入和/或输出可能不会自然地表示为序列，但是有一些数据不是序列形式的，Set2Set可以是从集合到集合。

注意：输出通道数是输入通道数的两倍
$\begin{align}\begin{aligned}\mathbf{q}_t &= \mathrm{LSTM}(\mathbf{q}^{*}_{t-1})\\\alpha_{i,t} &= \mathrm{softmax}(\mathbf{x}_i \cdot \mathbf{q}_t)\\\mathbf{r}_t &= \sum_{i=1}^N \alpha_{i,t} \mathbf{x}_i\\\mathbf{q}^{*}_t &= \mathbf{q}_t \, \Vert \, \mathbf{r}_t,\end{aligned}\end{align}$

set2set = Set2Set(dim, processing_steps=3)

out = self.set2set(out, data.batch)

GRU：
$r_t = \sigma(W_{ir} x_t + b_{ir} + W_{hr} h_{(t-1)} + b_{hr}) \\ z_t = \sigma(W_{iz} x_t + b_{iz} + W_{hz} h_{(t-1)} + b_{hz}) \\ n_t = \tanh(W_{in} x_t + b_{in} + r_t * (W_{hn} h_{(t-1)}+ b_{hn})) \\ h_t = (1 - z_t) * n_t + z_t * h_{(t-1)}$

rnn = nn.GRU(10, 20, 2)
input = torch.randn(5, 3, 10)
h0 = torch.randn(2, 3, 20)
output, hn = rnn(input, h0)

官网示例代码注释：

GitHub - pyg-team/pytorch_geometric: Graph Neural Network Library for PyTorch

import os.path as osp

import networkx as nx
import torch
import torch.nn.functional as F
from torch.nn import GRU, Linear, ReLU, Sequential

import torch_geometric.transforms as T
from torch_geometric.datasets import QM9
from torch_geometric.loader import DataLoader
from torch_geometric.nn import NNConv
from torch_geometric.nn.aggr import Set2Set
from torch_geometric.utils import remove_self_loops, to_networkx
import pylab

target = 0
dim = 64


class MyTransform(object):
    def __call__(self, data):
        # Specify target.
        data.y = data.y[:, target]
        return data


class Complete(object):
    def __call__(self, data):
        device = data.edge_index.device

        row = torch.arange(data.num_nodes, dtype=torch.long, device=device)
        col = torch.arange(data.num_nodes, dtype=torch.long, device=device)

        row = row.view(-1, 1).repeat(1, data.num_nodes).view(-1)
        col = col.repeat(data.num_nodes)
        edge_index = torch.stack([row, col], dim=0)

        edge_attr = None
        if data.edge_attr is not None:
            idx = data.edge_index[0] * data.num_nodes + data.edge_index[1]
            size = list(data.edge_attr.size())
            size[0] = data.num_nodes * data.num_nodes
            edge_attr = data.edge_attr.new_zeros(size)
            edge_attr[idx] = data.edge_attr

        edge_index, edge_attr = remove_self_loops(edge_index, edge_attr)
        data.edge_attr = edge_attr
        data.edge_index = edge_index

        return data


path = osp.join(osp.dirname(osp.realpath(__file__)), '..', 'data', 'QM9')
transform = T.Compose([MyTransform(), Complete(), T.Distance(norm=False)])
dataset = QM9(path, transform=transform).shuffle()

# 可视化分子
one_data = dataset[0]
G = to_networkx(one_data)
nx.draw(G)
pylab.show()

# Normalize targets to mean = 0 and std = 1.
mean = dataset.data.y.mean(dim=0, keepdim=True)
std = dataset.data.y.std(dim=0, keepdim=True)
dataset.data.y = (dataset.data.y - mean) / std
mean, std = mean[:, target].item(), std[:, target].item()

# Split datasets.
test_dataset = dataset[:10000]
val_dataset = dataset[10000:20000]
train_dataset = dataset[20000:]
test_loader = DataLoader(test_dataset, batch_size=128, shuffle=False)
val_loader = DataLoader(val_dataset, batch_size=128, shuffle=False)
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)


class Net(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.lin0 = torch.nn.Linear(dataset.num_features, dim)

        nn = Sequential(Linear(5, 128), ReLU(), Linear(128, dim * dim))
        self.conv = NNConv(dim, dim, nn, aggr='mean')
        self.gru = GRU(dim, dim)

        # Set2Set是一种将集合到集合用LSTM时序模型进行映射的聚合方式，注意out_channels = 2 * in_channels
        self.set2set = Set2Set(dim, processing_steps=3)
        self.lin1 = torch.nn.Linear(2 * dim, dim)
        self.lin2 = torch.nn.Linear(dim, 1)

    def forward(self, data):
        out = F.relu(self.lin0(data.x))
        h = out.unsqueeze(0)

        for i in range(3):
            m = F.relu(self.conv(out, data.edge_index, data.edge_attr))
            out, h = self.gru(m.unsqueeze(0), h)
            out = out.squeeze(0)
        # (2325,64)
        out = self.set2set(out, data.batch)
        # (128,128)
        out = F.relu(self.lin1(out))
        out = self.lin2(out)
        return out.view(-1)


device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min',
                                                       factor=0.7, patience=5,
                                                       min_lr=0.00001)


def train(epoch):
    model.train()
    loss_all = 0

    for data in train_loader:
        data = data.to(device)
        optimizer.zero_grad()
        loss = F.mse_loss(model(data), data.y)
        loss.backward()
        loss_all += loss.item() * data.num_graphs
        optimizer.step()
    return loss_all / len(train_loader.dataset)


def test(loader):
    model.eval()
    error = 0

    for data in loader:
        data = data.to(device)
        error += (model(data) * std - data.y * std).abs().sum().item()  # MAE
    return error / len(loader.dataset)


best_val_error = None
for epoch in range(1, 301):
    lr = scheduler.optimizer.param_groups[0]['lr']
    loss = train(epoch)
    val_error = test(val_loader)
    scheduler.step(val_error)

    if best_val_error is None or val_error <= best_val_error:
        test_error = test(test_loader)
        best_val_error = val_error

    print(f'Epoch: {epoch:03d}, LR: {lr:7f}, Loss: {loss:.7f}, '
          f'Val MAE: {val_error:.7f}, Test MAE: {test_error:.7f}')