一、背景

前文讲了RNN的基本原理，可以发现RNN是一个比较简单的神经网络结构，虽然为文本和时间序列的建模提供了一个很好的思路，但是也有一定的局限性。最直观的就是使用了Tanh函数造成梯度消失的问题。

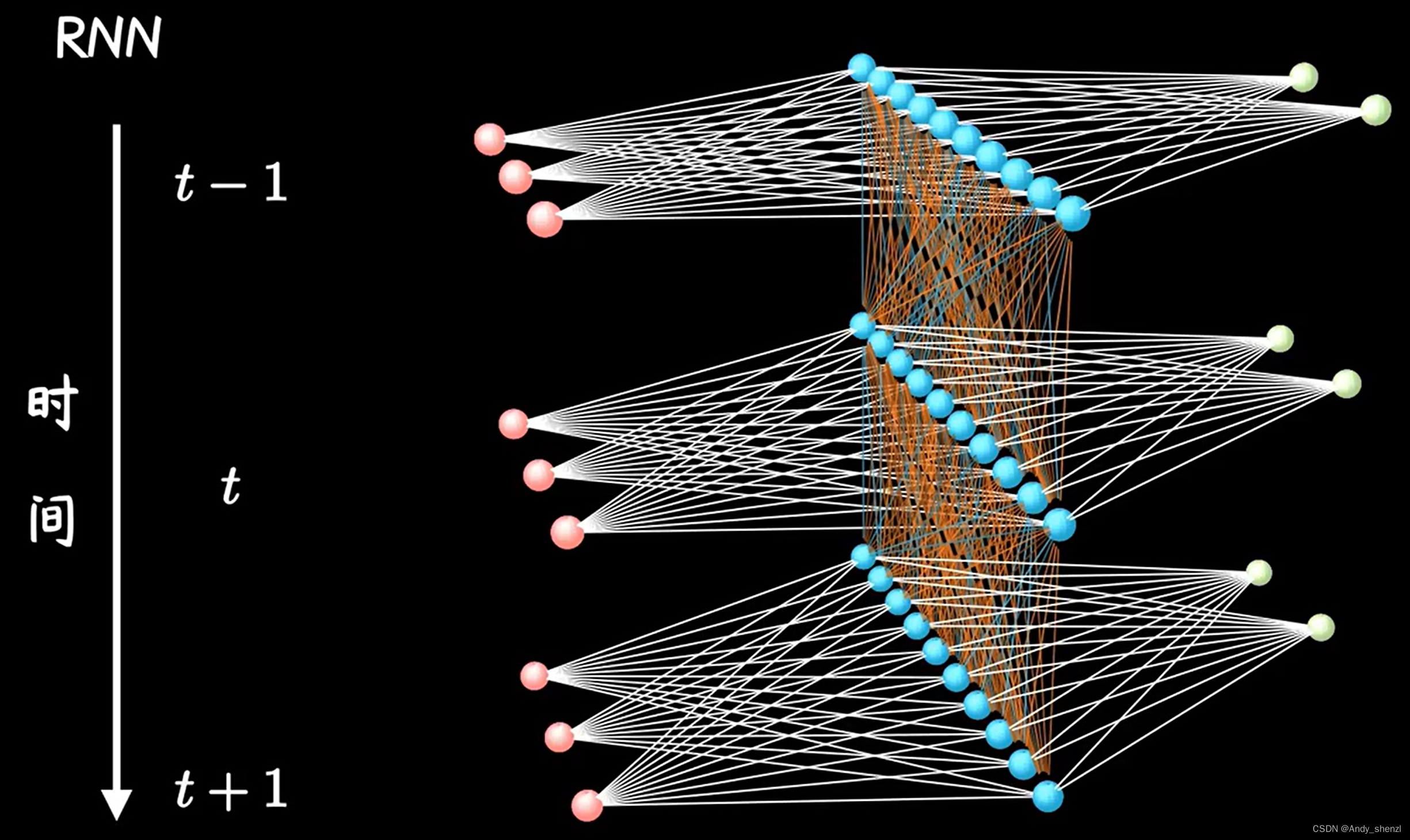
根据Tanh的性质，很容易出现一个现象就是激活函数结果太大，激活函数的绝对值在很接近于1的位置，而对应的激活函数的梯度就会接近于0 。这样，在沿着时间反向传播的过程中，梯度就会逐渐减小，知道非常接近于0，这样会导致一个直接的结果就是RNN会很容易遗忘，即隐含的状态很难描述长距离输入的依赖关系。

为防止这个现象的发生，LSTM和GRU这两种循环神经网络被开发出来，解决信息丢失问题。

二、LSTM原理

长短时记忆网络（Long Short-term Memory Network，LSTM），不同于RNN只能记忆短期的记忆$S_t$，LSTM隐含状态是两个状态，短期记忆$S_t$和长期记忆$C_t$

下面我们来解析下LSTM的网络结构

2.1 LSTM 网络结构

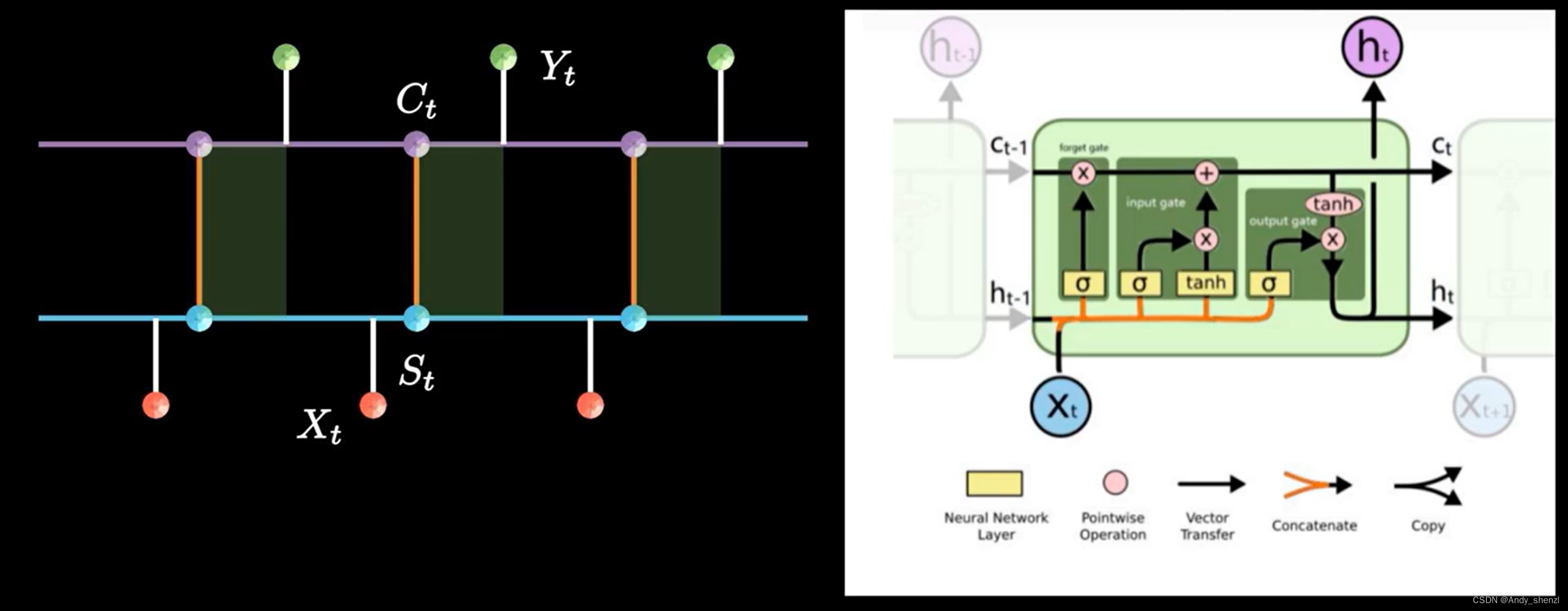
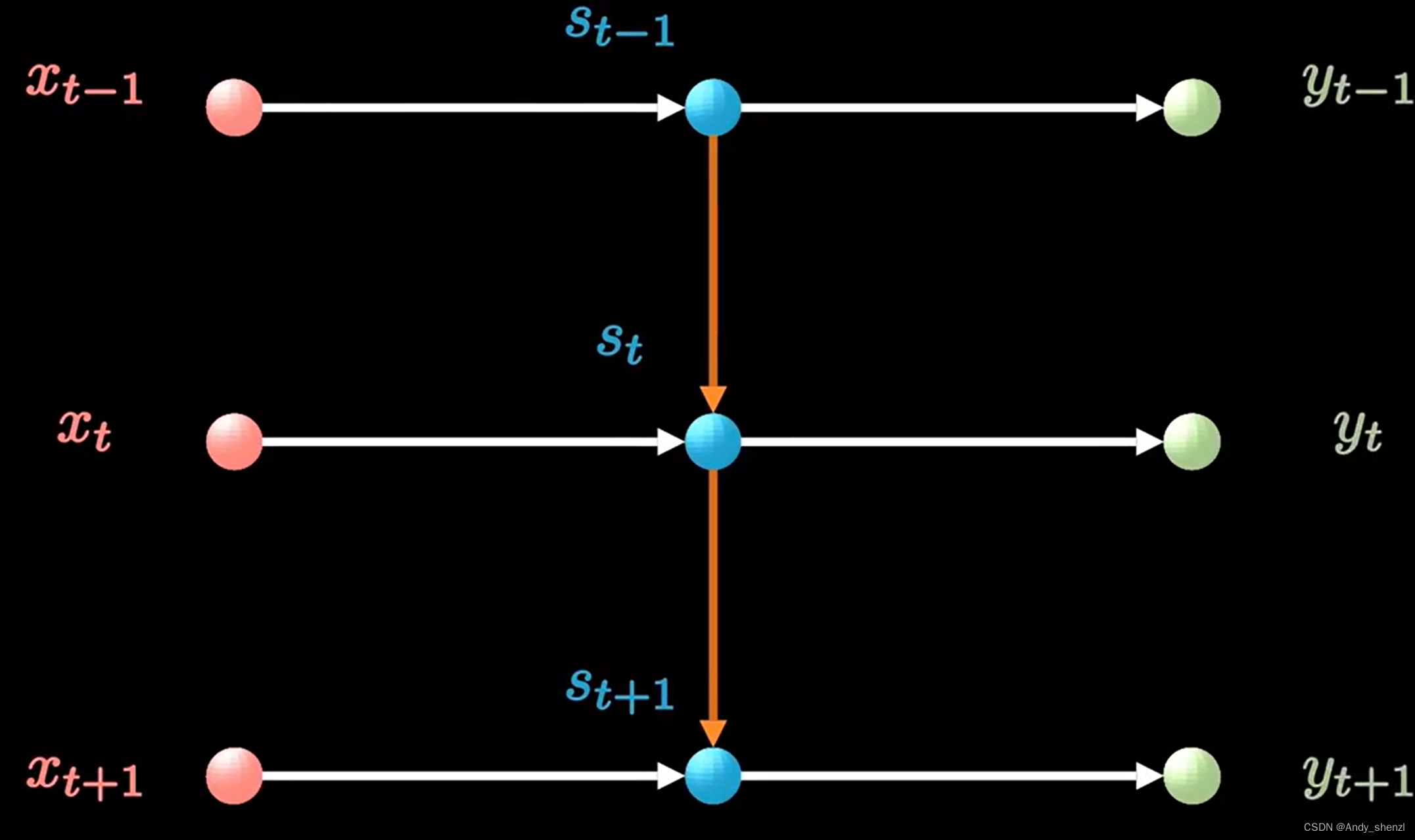
在RNN中，如下图，左边红色是不同时刻的输入X，中间的蓝色部分是隐层状态S，右边绿色是网络输出Y

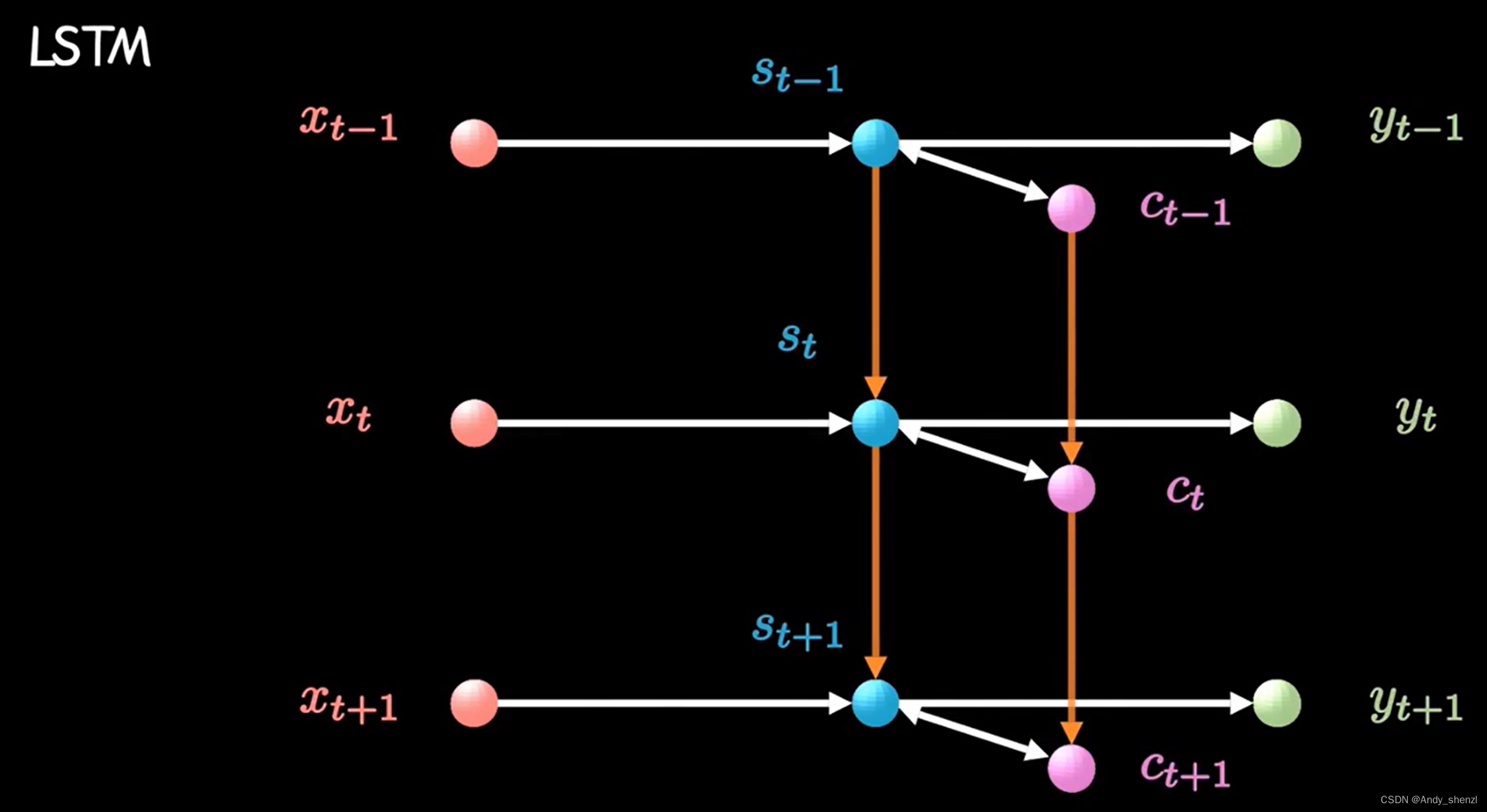
LSMT加了一条新的时间链C，同时增加了两条链之间的关联关系，如下图

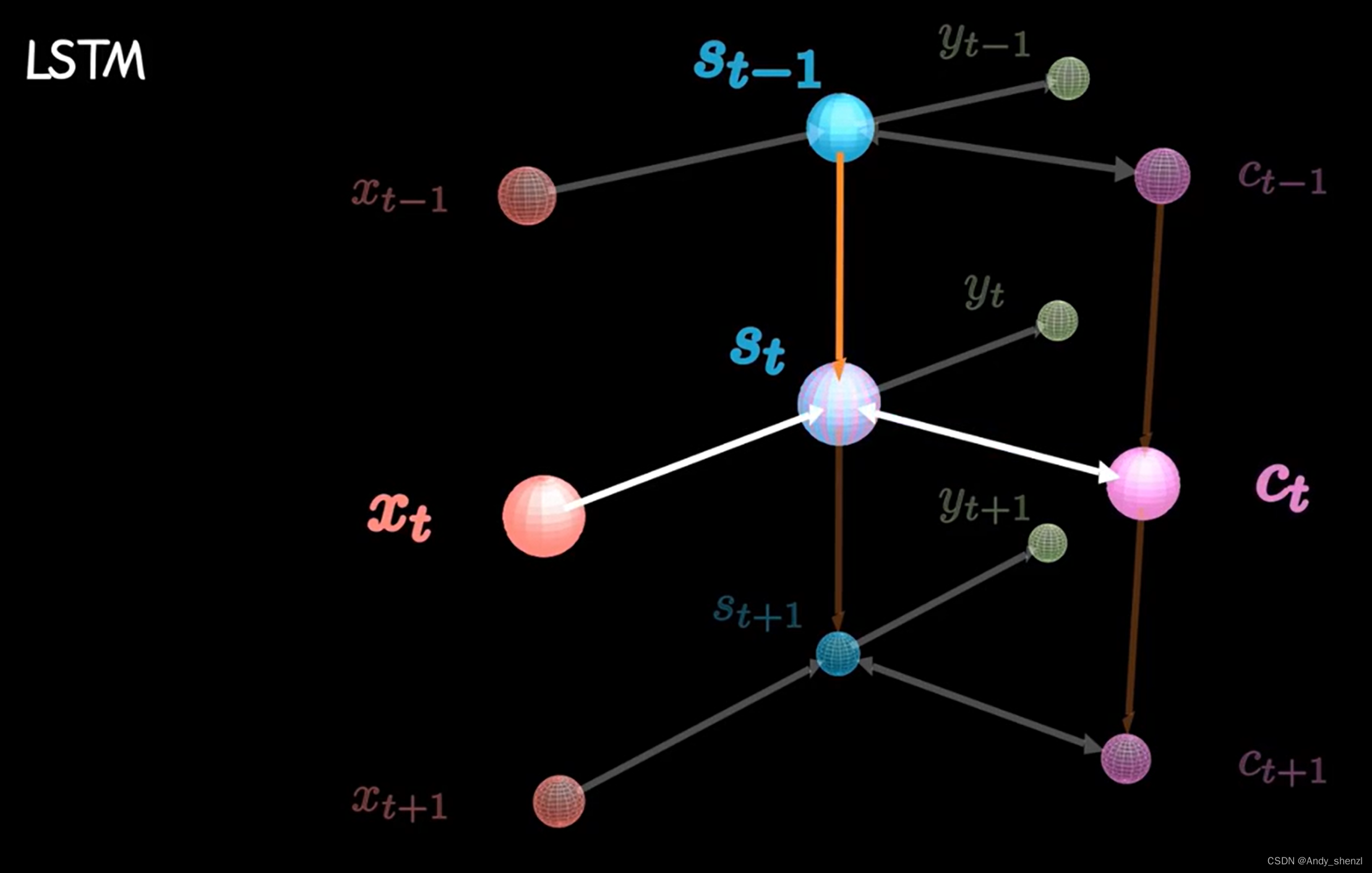
计算隐藏状态$S_t$时，除了输入$X_{t-1}$和前一时刻，还要包含当前时刻的信息$C_t$

2.2 LSTM解析

把$S_t$和$C_t$间的关联放大看，把一条线拆成三条线，包含了两步更加细致的操作

• 需要遗忘的信息
• 需要记住的信息

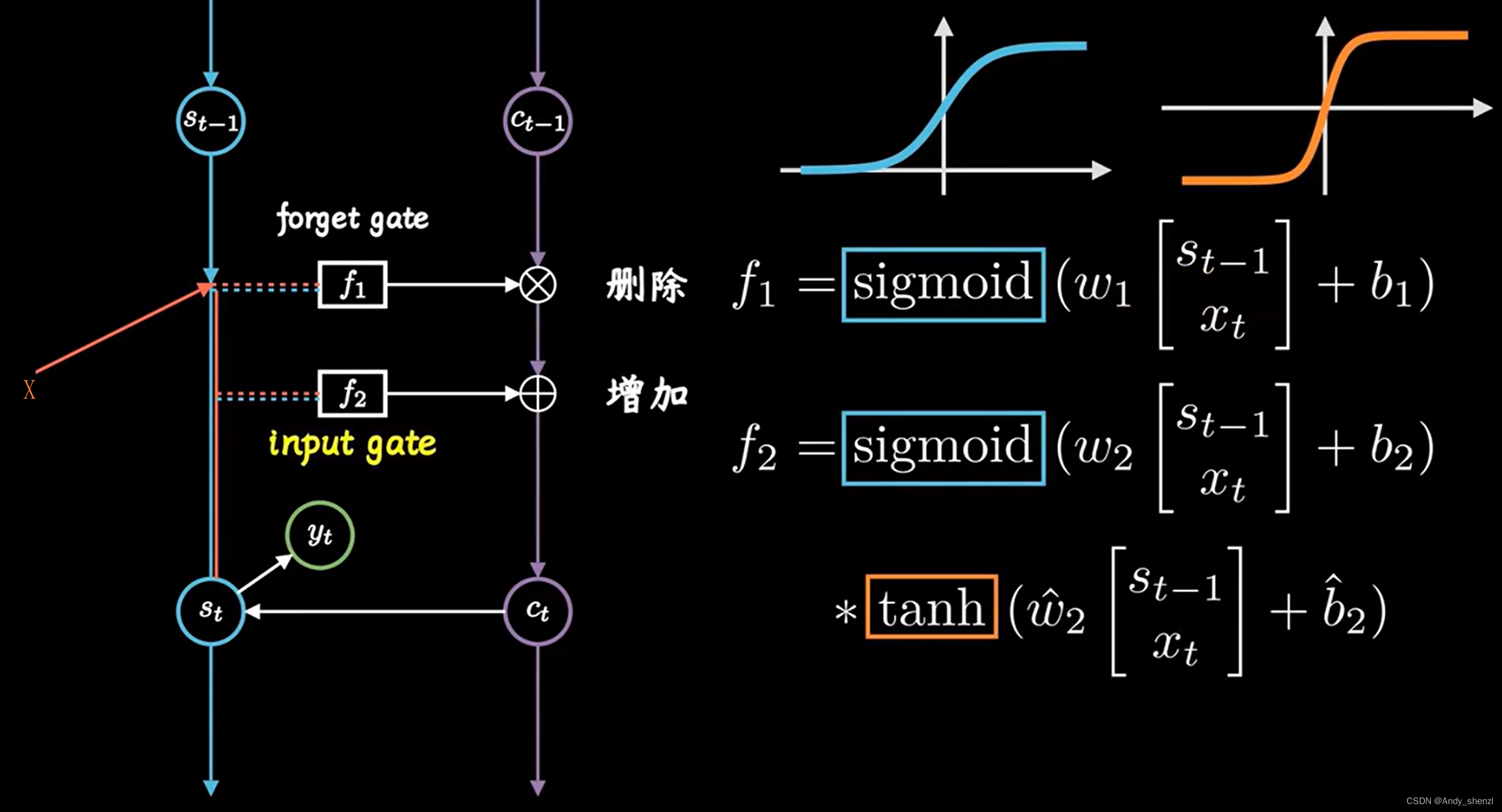
• 遗忘门
  函数$f_1$就像一个橡皮擦，根据上一时刻的记忆$S_{t-1}$和今天输入$x_t$，决定要修改哪些信息，用数学语言描述就是$f_1=sigmoid(w_1\left[\begin{array}{c}{S}_{t-1}\\ x_t\end{array}\right]+b_1)$，我们知道，sigmoid函数的取值在[0,1]之间，矩阵元素相乘时会抹掉那些取值为0的元素，相当于选择性遗忘了部分记忆（具体哪些需要进行选择遗忘就是模型训练的目标），这个就被成为forget gate，即遗忘门，就像一个阀门一样过滤重要特征，忽略无关信息；

• 记忆门
  函数$f_2$就像一支笔，再次根据上一时刻的记忆$S_{t-1}$和今天输入$x_t$，决定要在信息里面保留哪些信息，数学语言描述就是$f_2=sigmoid(w_2\left[\begin{array}{c}{S}_{t-1}\\ x_t\end{array}\right]+b_2)\ast tanh({\hat{w}}_2\left[\begin{array}{c}{S}_{t-1}\\ x_t\end{array}\right]+{\hat{b}}_2)$，其中sigmoid函数再次对信息进行选择，tanh函数取值在[-1, 1]之间，这不操作不是遗忘，而是相当于把$x_{t-1}$和$x_t$这两个时刻的信息进行梳理和归纳，因此被称为input gate ，记忆门

• 更新
  把两步操作合起来，用公式表示就是$C_t=f_1\ast C_{t-1}+f_2$，对应上图，就是先相乘再相加，这样就得到了新的$C_t$，他除了会继续向下传递，同时还会被用来更新当前短期记忆$S_t$，最后我们就可以计算输出得到$y_t$，同时保持记忆短期记忆$S_t$和长期记忆$C_t$，并且相互更新，以上就是LSTM的原理

大多数关于LSTM文章的解析习惯用下图右边的图进行解释，里面内容看起来很多，理解起来也比较困难，所以我们把左右量还在那个图对照一下，再根据上面的解释，再去理解应该就简单了