目录
1. 著名无限积公式简述及证明
2. Jules Lissajous 和他的图形(Jules Lissajous and His Figures)
11章 一个著名的公式
The prototype of all infinite processes is repetition. . . .
Our very concept of the infinite derives from the notion
that what has been said or done once can always be
repeated.
(所有无限过程的原型是重复……我们对无限的概念源自曾经所说或做过的概念,总是可以重复。)
——Tobias Dantzig,<< Number: The Language of Science>>(数:科学的语言)
1. 著名无限积公式简述及证明
我们还没有完全理解函数(sin x)/x。有一天,浏览一本数学公式手册,我遇到了如下的等式:
。---------------------------------(1)
因为我以前从未见过这个公式,所以我预计证明会相当困难。令我惊讶的是,它原来非常简单:
重复这个过程n次之后,我们得到
。
我们将式子改写一下,其中,x≠0,得到
。
请注意,我们已经颠倒了(因为仍是有限的)乘积中剩余项的顺序。假如我们现在保持x不变,而n->∞,则 , 而方括号中的表达式,符合sin α/α公式的形式,趋近于1。因此,我们得到
其中,Π表示乘积。两边除以x,我们得到等式(1)。
方程(1)由Euler[1]发现,代表了初等数学中无限乘积(infinite product)的极少数例子之一。因为等式对于所有x值都成立(如果我们定义sin 0/0 = 1的话,则也包括x = 0),我们可以代入一个值,比如,x = π/2:
现在, 以及
。对剩余的项使用半角公式
,稍微简化之后,我们得到
这个漂亮的公式是由Vi`ete在1953年发现的;在建立它时,他使用了一个几何论证,该论证基于同一圆内接的 n 条边和 2n 条边的正多边形的面积比。[2] Vi`ete的公式标志着数学史上的一个里程碑:它是第一次将无限过程明确地写成一系列代数运算。(直到那时,数学家们都小心翼翼地避免直接提及无限过程,而是将它们视为可以重复任意多次的有限连续操作。) 通过在他的乘积末尾添加三个点, Vi`ete大胆地宣布无限是数学的真正组成部分。 这标志着现代意义上的数学分析的开始。
除了其美妙之外,Vi`ete公式的著名之处还在于,它允许我们通过反复使用算术的四个基本运算——加法、乘法、除法和开方(square root extraction),去求得数π的值——所有的运算都是应用到数2上。甚至可以通过最简单的科学计算实现:
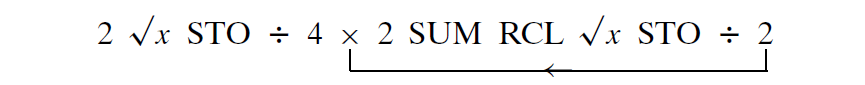
(在某些计算器上,内存操作STO,RCL,以及SUM分别标为M,RM和M+)。每一次迭代,你都可以通过以上所示的键排列中,按x键并松开之后迅速按1/x键,从而读出当前计算所得的π的近似值;在第九轮迭代之后,我们得到了π的一个近似值3.1415914——精确到小数点后5位的值。当然,可编程计算器会大大加快速度。
从收敛的角度考察等式(1)是有启动性的(instructive)。我们注意到,首先,部分乘积的收敛对于它们的极限值而言是单调的(monotonic);也就是说,每增加一项,我们就更接近极限。这是因为每一项都是小于1的数,导致部分乘积的值不断递减。这对sinx/x而言,其与无限级数(infinite series)形成鲜明的对比:
其自顶向下交替接近其极限值。此外,尽管在某种程度上它比级数收敛慢一些,它的收敛速度也非常快。下表5对比了x = π/2时等式(1)和等式(2)的收敛速率:
表5
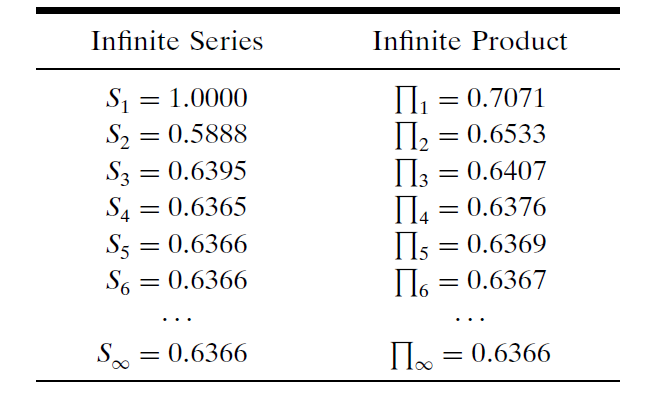
注意:所有的数字都四舍五入到小数点后四位。
无穷乘积快速收敛的原因可以从图68中看出。在单位圆上,我们用角度θ/2,(θ/2 + θ/4),(θ/2 + θ/4 + θ/8),等等,划分出半径。这些角组成了一个无限几何级数,其和为θ/2 + θ/4 + θ/8 + ... = θ 。现在,以x轴开始,我们从一条半径向下一条半径依次作垂直投影。这些垂直投影的长度依次为1,cos(θ/2),cos(θ/2). cos(θ/4) ,cos(θ/2). cos(θ/4). cos(θ/8),如此等等。仅经过几步之后,我们就可以看出,投影值就与其最终值几乎没有区别。
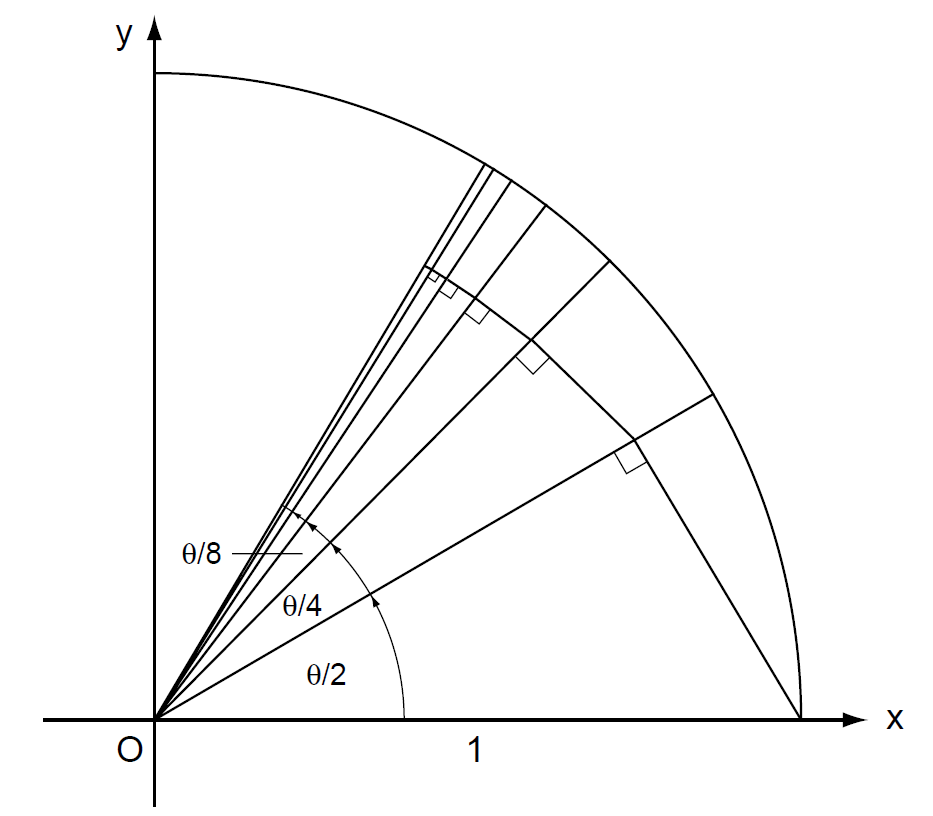
图68 无穷乘积的收敛性
遵循每个三角恒等式都可以几何解释的原则,我们现在问我们可以赋予等式(1)什么几何意义。答案如图 69 所示。我们以圆心位于坐标原点半径为 的圆开始。从x轴开始,我们标出一个角θ , 它的另一边与圆相切于
点,现在我们将
点和
点连接起来,
点的坐标为(
,0), 用
标识线段
。角
的顶点位于通过
且与角θ对应同一段弧的圆的圆上,其角大小等于θ/2。对角
应用正弦法则,我们有
但是,sin(180°- θ) = sin(θ) = 2sin(θ/2)cos(θ/2);将这个等式代入等式(3)并对 解方程,我们得到
。
我们现在以 为圆心为
半径画出第二个圆。我们有
,重复画第一个圆的这些步骤直到完成,并应用正弦法则到三角形
, 得到
,其中
。重复这个过程n次,我们得到以
为圆心
为半径的圆。解方程得
现在,因此,应用正弦法则到三角形
得到
;因此,
在(4)和(5)之间消除掉 和
,我们得到
随着n无限制地增加,无限趋近于0, 因此与其正弦值没有区别;换句话说,半径为
的弧,趋近于从
到x轴的垂线。则,用
替换掉
并消除掉因子
,用x替换掉θ,我们得到等式(1)。
因此,等式(1)是以下定理的三角表现形式,即内接于圆的角等于对向同一圆弧的圆心角的二分之一,一次又一次地重复,得到越来越小的角内接于越来越大的圆中。[3]
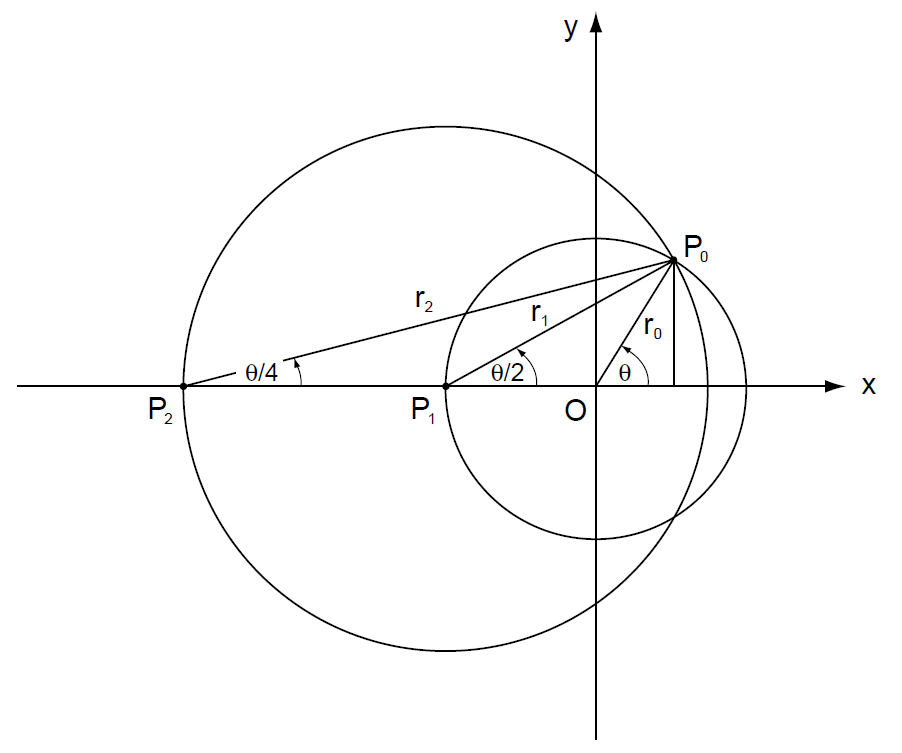
图69 公式的几何证明
注释与资料来源:
(本章节基于我的文章“A Remarkable Trigonometric Identity(一个著名的三角桓等式)”),Mathematics Teacher(数学教师杂志),卷70,编号5(1997年5月),第452-455页。
1. E. W. Hobson,<<Squaring the Circle: A History of the Problem>>(化圆为方:这个问题的历史), (Cambridge,England: Cambridge University Press, 1913),第26页。
2. 参见Petr Beckmann,<< A History of π>>(一段π的历史)( Boulder, Colo.: Golem Press,1977)。
3. 上述文章给出了基于物理考虑的等式(1)的证明。
2. Jules Lissajous 和他的图形(Jules Lissajous and His Figures)
Jules Antoine Lissajous (1822–1880)并不是科学史上的巨人,但他的名字通过“Lissajous图形(Lissajous figures)”而为物理专业的学生所熟知——Lissajous图形是两个沿垂直(perpendicular)直线的振动(vibrations)叠加(superimposed)时形成的图案。Lissajous于 1841年进入巴黎高等师范学院,后来成为巴黎 Lyc´ee Saint-Louis 的物理学教授,在那里他研究振动和声音。1855 年,他发明了一种研究复合振动的简单光学方法:他在每个振动物体(例如两个音叉(running forks))上安装一个小镜子,然后将一束光对准其中一个镜子。 光束首先被反射到另一个镜子,然后反射到一个大屏幕,在那里它形成了一个二维图案,这是两种振动结合的视觉结果。这个简单的想法——现代示波器的先驱——在Lissajous的时代是一个新奇事物,因为在那之前,对声音的研究完全依赖于听觉过程,即人耳。 Lissajous 确实使“看到声音”成为可能。
设每次振动都是以正弦波表示的简谐运动;令a和b表示振幅,和
表示角频率(以弧度/秒为单位),
和
表示相位,t 表示时间。然后我们有
随着时间的推移,点P(其坐标为(x, y))将会绘制一条曲线,其方程可以通过消除(1)中的t而得到。因为这两个方程包含6个参数[1],曲线除了某些特殊情况外,往往非常复杂。例如,假如 且
,我们有
在其中,我们已经去除了参数的下标。为了消除掉这些方等式国的时间t,我们注意到,x / a = y /b,因此,y = (b /a) x ,这是一条直线的方程。类似地,对于和相位差π,我们得到直线y = -(b /a) x 。对于ω1
![]() = ω2
= ω2![]() 和相位差π/2 ,我们得到(取
和相位差π/2 ,我们得到(取)
x = a sin(ωt),y = b sin(ωt + π/2) = b cos(ωt ) 。
用a除以第一个等式,用b除以第二个等式,对结果平方再加相,我们得到
它表示一个椭圆,其轴沿x轴和y轴(如果再加上条件a=b,则椭圆成了一个圆)。对于任意相伴差而言,曲线将是一个倾斜的(tilted)椭圆,前面的例子是一个特例(直线y =±(b /a) x是一个退化的(degenerate)椭圆)。如果我们让相位差连续变化,椭圆会慢慢改变它的方向和形状,从圆(a = b这种情况) 到直线y =±x穿过然后再返回(图70)。
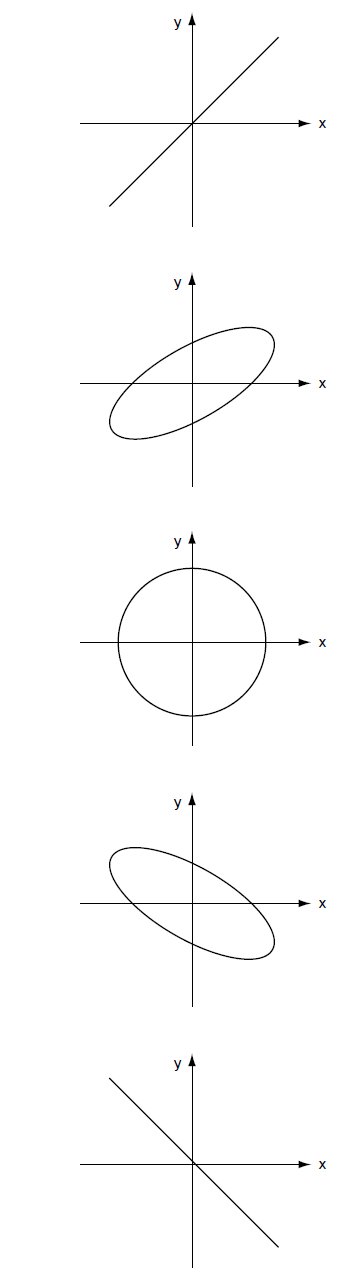
--------------图70 Lissajous图形,![]() =
= ![]() 的情况------------------------------
的情况------------------------------
假如角频率不相等,则曲线更为复杂。例如,如果![]() = 2
= 2![]() (从音乐上来讲,当两个振动相隔一个八音(an octave apart)时),我们有
(从音乐上来讲,当两个振动相隔一个八音(an octave apart)时),我们有
其中我们又去掉下标,并取 。现在我们获得的这种曲线取决于Φ。对于Φ = π/2,我们有
。
使用恒等式 并消除两个方程之间的时间t,得到结果
。该方程表示一条抛物线(parabola),点 P 沿该抛物线随着时间的推移来回移动。对于Φ的其它值,曲线可能是一种封闭的形状(图71)。

--------------图71 Lissajous图形, 的情况-----------------------------
另一个观察到的现象也值得一提。只要角频率比率是一个比率数,曲线——无论多么复杂——最终都将自我重复,引起运动周期化。[2] 但是,如果
是一个非比率数,P将永远不会重绘它的路径,导致非周期性的运动。然而,随着时间的推进,曲线将渐渐填满直线x = ±a,y=±b围成的矩形边界(图72)。
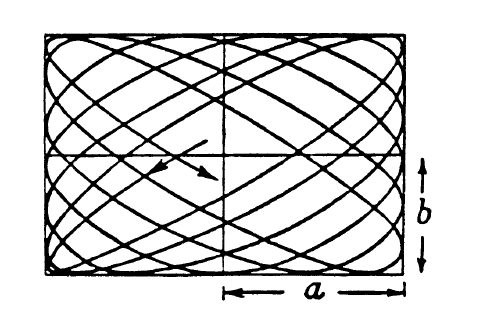
--------------图72 Lissajous图形,是非比率数的情况------------------------------------------
Lissajous 的工作受到同时代人的赞扬,物理学家John Tyndall(1820-1893年)和John William Strutt(1842-1919年)在他们关于声学的经典论文中对此进行了讨论。1873年,他因“美丽的实验”获得了著名的(prestigious)拉卡兹奖(Lacaze Prize),他的方法在1867年的巴黎万国博览会上展出。但显然太阳底下没有新鲜事:Lissajous的图形早在很久以前就被自学成长的美国科学家Nathaniel Bowditch(1773-1838 年)教授发现了,他于1815年用复摆制造了它们。[3] 该装置的一种变体,其中两个摆的运动结合在一起,并通过附在其中一个摆上的笔在纸上描绘出来钟摆,成为 19 世纪流行的科学演示(图 73); 随后的图形被称为“谐波图(harmonograms)”,它们令人难以置信的多样性总是给观众留下深刻印象(图 74)。[4] Lissajous方法的新颖之处在于它脱离了机械设备,而是依赖于效率更高的光代理。在这方面,他是一个有远见的人,预言了我们的现代电子时代。

--------------图73 谐波记录器,来自17世纪的科技图书---------------------
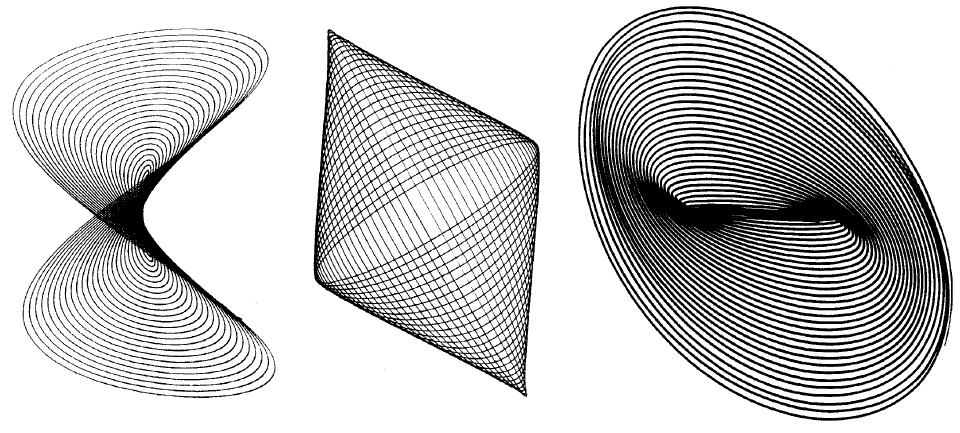
------------------------------图74谐波图--------------------------------
1. 事实上,5个参数足够了,因为只有相对相位(relative phase)(即相位差)起重要作用。
2. 该周期将是两个单独周期的最小公倍数(the least common multiple)。
3. Florian Cajori, <<A History of Physics>> (1898年初版, 1928年修订版; New York: Dover, 1962重印), 第288–289页。
4. 1980 年,我和同事Wilbur Hoppe在威斯康星大学欧克莱尔分校的数学模型研讨会上制作了一个复摆(compound pendulum)。图74中所示的图案是使用该设备生成的。
内容来源:
<<Trigonometric Delights>> 作者:Eli Maor