如何提升 ETF 期权隐含波动率和希腊值的计算速度？

news2024/9/30 19:39:26

期权的隐含波动率可以反应市场对未来的预期，通常使用牛顿法和二分法来计算。这两种方法都需要频繁迭代，且迭代次数不能确定，核心代码无法向量化，因此只能通过循环来逼近求解。这就导致在期权相关计算中，隐含波动率往往容易成为性能的瓶颈。

DolphinDB 的计算逻辑使用脚本语言编写，但底层调用的是 C++ 代码，存在脚本解释的过程。为了提高脚本的执行效率，DolphinDB 从 1.01 版本开始支持即时编译（JIT）功能，特别适合于无法使用向量化运算但又对运行速度有极高要求的场景。

本教程将基于客户的实际需求，以二分法计算 ETF 期权的隐含波动率及希腊值为例，为大家示范如何使用 DolphinDB 的 JIT 功能给计算过程加速，并与 C++ 原生代码进行了计算性能对比测试，结果表明 DolphinDB 脚本计算耗时为 C++ 原生代码的1.5倍。

1. 数据表结构

1.1 期权日频数据表

字段

字段类型

含义

tradedate

DATE

交易日期

sym

SYMBOL

标的代码

codes

SYMBOL

期权合约代码

closeprice

DOUBLE

日收盘价格

etf

SYMBOL

期权合成价格的两个合约代码

etfprice

DOUBLE

期权合成价格

字符串字段使用 SYMBOL 类型和 STRING 类型存储的差异，参考： 数据类型 — DolphinDB 2.0 文档的字符串部分内容。

期权日频数据表在 DolphinDB 中存储时，建议在时间维度按年分区即可，创建库表的代码如下：

login("admin", "123456")
dbName = "dfs://optionPrice"
tbName = "optionPrice"
if(existsDatabase(dbName)){
	dropDatabase(dbName)
}
db = database(dbName, RANGE, date(datetimeAdd(2000.01M,0..50*12,'M')))
colNames = `tradedate`sym`codes`closeprice`etf`etfprice
colTypes = [DATE, SYMBOL, SYMBOL, DOUBLE, SYMBOL, DOUBLE]
schemaTable = table(1:0, colNames, colTypes)
db.createPartitionedTable(table=schemaTable, tableName=tbName, partitionColumns=`tradedate)

读取 50 ETF 日频数据，代码如下：

data = select * from loadTable("dfs://optionPrice", "optionPrice") where sym =`510050

data 是表变量，具体数据内容如下图所示：

通过 panel 函数对 data 进行透视操作，将窄表数据展成矩阵，生成期权日收盘价矩阵，代码如下：

closPriceWideMatrix = panel(data.codes, data.tradeDate, data.closePrice)

closPriceWideMatrix 是矩阵变量，具体数据内容如下图所示：

通过 panel 函数对 data 进行透视操作，将窄表数据展成矩阵，生成期权合成价格矩阵，代码如下：

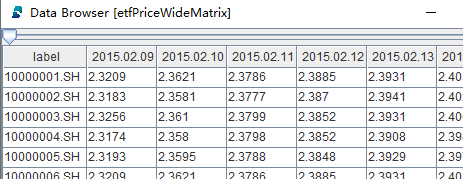
etfPriceWideMatrix = panel(data.codes, data.tradeDate, data.etfprice)

etfPriceWideMatrix 是矩阵变量，具体数据内容如下图所示：

1.2 期权信息

字段

字段类型

含义

code

STRING

期权合约代码

name

STRING

期权合约名称

exemode

INT

期权类型（认购认沽类型）

exeprice

DOUBLE

行权价

startdate

DATE

开始日期

lastdate

DATE

结束日期

sym

SYMBOL

标的代码

exeratio

DOUBLE

乘数

exeprice2

DOUBLE

分红后的行权价

dividenddate

DATE

分红日

tradecode

STRING

交易代码

期权信息数据在 DolphinDB 中存储时，建议在证券代码维度按值分区即可，创建库表的代码如下：

login("admin", "123456")
dbName = "dfs://optionInfo"
tbName = "optionInfo"
if(existsDatabase(dbName)){
	dropDatabase(dbName)
}
db = database(dbName, VALUE, `510050`510300)
colNames = `code`name`exemode`exeprice`startdate`lastdate`sym`exeratio`exeprice2`dividenddate`tradecode
colTypes = [STRING, STRING, INT, DOUBLE, DATE, DATE, SYMBOL, DOUBLE, DOUBLE, DATE, STRING]
schemaTable = table(1:0, colNames, colTypes)
db.createPartitionedTable(table=schemaTable, tableName=tbName, partitionColumns=`sym)

读取数据：

contractInfo = select * from loadTable("dfs://optionInfo", "optionInfo") where sym =`510050

contractInfo 是表变量，具体数据内容如下图所示：

1.3 交易日历

字段

字段类型

含义

tradedate

DATE

交易日期

交易日历存放在单列 csv 文件中，可以使用 DolphinDB 的 loadText 函数接口直接读取：

//交易日历csv文件路径
tradingDatesAbsoluteFilename = "/hdd/hdd9/tutorials/jitAccelerated/tradedate.csv"
startDate = 2015.02.01
endDate = 2022.03.01
//读取csv文件
allTradingDates = loadText(tradingDatesAbsoluteFilename)
//生成交易日向量
tradingDates = exec tradedate from allTradingDates where tradedate<endDate and tradedate >startDate

allTradingDates 是表变量，可以使用 exec 函数将表中的某一列转成向量变量，tradingDates 是向量变量。

2. 计算函数代码开发

2.1 隐含波动率

DolphinDB 脚本语言需要先解释再执行，计算密集的代码如果不能向量化，在脚本层面使用 while 和 for 循环以及条件分支，就会比较耗时。期权隐含波动率计算的步骤，由于使用了上下限值循环逼近的二分法，正是需要 JIT 加速的计算类型。以下就是二分法逼近隐含波动率的代码：

@jit
def calculateD1JIT(etfTodayPrice, KPrice, r, dayRatio, HLMean){
	skRatio = etfTodayPrice / KPrice
	denominator = HLMean * sqrt(dayRatio)
	result = (log(skRatio) + (r + 0.5 * pow(HLMean, 2)) * dayRatio) / denominator
	return result
}

@jit
def calculatePriceJIT(etfTodayPrice, KPrice , r , dayRatio , HLMean , CPMode){
	testResult = 0.0
	if (HLMean <= 0){
		testResult = CPMode * (etfTodayPrice - KPrice)
		if(testResult<0){
			return 0.0
		}
		return testResult
	}
	d1 = calculateD1JIT(etfTodayPrice, KPrice, r, dayRatio, HLMean)
	d2 = d1 - HLMean * sqrt(dayRatio)
	price = CPMode * (etfTodayPrice * cdfNormal(0, 1, CPMode * d1) - KPrice * cdfNormal(0, 1, CPMode * d2) * exp(-r * dayRatio))
	return price
}

@jit
def calculateImpvJIT(optionTodayClose, etfTodayPrice, KPrice, r, dayRatio, CPMode){
	v = 0.0	
	high = 2.0
	low = 0.0
	do{
		if ((high - low) <= 0.00001){
			break
		}
		HLMean = (high + low) / 2.0
		if (calculatePriceJIT(etfTodayPrice, KPrice, r, dayRatio, HLMean, CPMode) > optionTodayClose){
			high = HLMean
		}
		else{
			low = HLMean
		}
	}
	while(true)
	v = (high + low) / 2.0
	return v
}

def calculateImpv(optionTodayClose, etfTodayPrice, KPrice, r, dayRatio, CPMode){
	originalShape = optionTodayClose.shape()
	optionTodayClose_vec = optionTodayClose.reshape()
	etfTodayPrice_vec = etfTodayPrice.reshape()
	KPrice_vec = KPrice.reshape()
	dayRatio_vec = dayRatio.reshape()
	CPMode_vec = CPMode.reshape()
	impvTmp = each(calculateImpvJIT, optionTodayClose_vec, etfTodayPrice_vec, KPrice_vec, r, dayRatio_vec, CPMode_vec)	
	impv = impvTmp.reshape(originalShape)	
	return impv
}

calculateImpvJIT 是计算隐含波动的核心代码，其入参 optionTodayClose, etfTodayPrice, KPrice, r, dayRatio, CPMode 都是标量对象，其调用的 calculatePriceJIT 函数和 calculateD1JIT 函数都通过 @jit 装饰器的方式封装成JIT函数，以达到加速计算的目的。

calculateImpv 是计算隐含波动的最终调用函数，其入参 optionTodayClose, etfTodayPrice, KPrice, dayRatio, CPMode 都是矩阵对象，其主要作用是把输入和输出进行矩阵和向量的转换，以适不同函数的入参和输出。在后面 delta, gamma, vega, theta 计算时，也会用到这些矩阵入参，这里以 2015年2月16日的 50ETF 为例进行展示。

  • optionTodayClose

  • etfTodayPrice

  • KPrice

  • dayRatio

  • CPMode

2.2 delta

delta 表示期权价格对标的资产价格的变动率，即标的资产价格每变动一个单位，期权价格产生的变化。

delta 的计算可以方便地实现向量化计算，所以不需要调用 JIT 功能，其代码如下：

def calculateD1(etfTodayPrice, KPrice, r, dayRatio, HLMean){
	skRatio = etfTodayPrice / KPrice
	denominator = HLMean * sqrt(dayRatio)
	result = (log(skRatio) + (r + 0.5 * pow(HLMean, 2)) * dayRatio) / denominator
	return result
}

def cdfNormalMatrix(mean, stdev, X){
	originalShape = X.shape()
	X_vec = X.reshape()
	result = cdfNormal(mean, stdev, X_vec)
	return result.reshape(originalShape)
}

def calculateDelta(etfTodayPrice, KPrice, r, dayRatio, impvMatrix, CPMode){
	delta = iif(
			impvMatrix <= 0,
			0,
			0.01*etfTodayPrice*CPMode*cdfNormalMatrix(0, 1, CPMode * calculateD1(etfTodayPrice, KPrice, r, dayRatio, impvMatrix))
		)
	return delta
}

calculateDelta 是计算 delta 的最终调用函数，其入参 etfTodayPrice, KPrice, dayRatio, impvMatrix, CPMode 都是矩阵对象。

2.3 gamma

gamma 表示 delta 对于标的资产价格的变动率，即标的资产价格每变动一个单位，delta 值产生的变化。

gamma 的计算可以方便地实现向量化计算，所以不需要调用 JIT 功能，其代码如下：

def normpdf(x){
	return exp(-pow(x, 2)/2.0)/sqrt(2*pi)
}

def calculateD1(etfTodayPrice, KPrice, r, dayRatio, HLMean){
	skRatio = etfTodayPrice / KPrice
	denominator = HLMean * sqrt(dayRatio)
	result = (log(skRatio) + (r + 0.5 * pow(HLMean, 2)) * dayRatio) / denominator
	return result
}

def calculateGamma(etfTodayPrice, KPrice, r, dayRatio, impvMatrix){
	gamma = iif(
			impvMatrix <= 0,
			0,
			(normpdf(calculateD1(etfTodayPrice,  KPrice, r, dayRatio, impvMatrix)) \ (etfTodayPrice * impvMatrix * sqrt(dayRatio))) * pow(etfTodayPrice, 2) * 0.0001
		)	
	return gamma
}

calculateGamma 是计算 gamma 的最终调用函数，其入参 etfTodayPrice, KPrice, dayRatio, impvMatrix 都是矩阵对象。

2.4 vega

vega 表示波动率单位变动对期权价格产生的变化。

vega 的计算可以方便地实现向量化计算，所以不需要调用 JIT 功能，其代码如下：

def normpdf(x){
	return exp(-pow(x, 2)/2.0)/sqrt(2*pi)
}

def calculateD1(etfTodayPrice, KPrice, r, dayRatio, HLMean){
	skRatio = etfTodayPrice / KPrice
	denominator = HLMean * sqrt(dayRatio)
	result = (log(skRatio) + (r + 0.5 * pow(HLMean, 2)) * dayRatio) / denominator
	return result
}

def calculateVega(etfTodayPrice, KPrice, r, dayRatio, impvMatrix){
	vega = iif(
			impvMatrix <= 0,
			0,
			etfTodayPrice * normpdf(calculateD1(etfTodayPrice, KPrice, r, dayRatio, impvMatrix)) * sqrt(dayRatio)
		)
	return vega \ 100.0
}

calculateVega 是计算 vega 的最终调用函数，其入参 etfTodayPrice, KPrice, dayRatio, impvMatrix 都是矩阵对象。

2.5 theta

theta 表示时间流逝对期权价格产生的变化，即每减少一天，期权价格的变化值。

theta 的计算可以方便地实现向量化计算，所以不需要调用 JIT 功能，其代码如下：

def calculateD1(etfTodayPrice, KPrice, r, dayRatio, HLMean){
	skRatio = etfTodayPrice / KPrice
	denominator = HLMean * sqrt(dayRatio)
	result = (log(skRatio) + (r + 0.5 * pow(HLMean, 2)) * dayRatio) / denominator
	return result
}

def normpdf(x){
	return exp(-pow(x, 2)/2.0)/sqrt(2*pi)
}

def cdfNormalMatrix(mean, stdev, X){
	originalShape = X.shape()
	X_vec = X.reshape()
	result = cdfNormal(mean, stdev, X_vec)
	return result.reshape(originalShape)
}


def calculateTheta(etfTodayPrice, KPrice, r, dayRatio, impvMatrix, CPMode){
	annualDays = 365
	d1 = calculateD1(etfTodayPrice, KPrice, r, dayRatio, impvMatrix)
	d2 = d1 - impvMatrix * sqrt(dayRatio)
	theta = (-etfTodayPrice * normpdf(d1) * impvMatrix \ (2 * sqrt(dayRatio)) - CPMode * r * KPrice * exp(-r * dayRatio) *cdfNormalMatrix(0, 1, CPMode * d2)) \ annualDays
	result = iif(impvMatrix<= 0, 0, theta)	
	return result
}

calculateTheta 是计算 theta 的最终调用函数，其入参 etfTodayPrice, KPrice, dayRatio, impvMatrix, CPMode 都是矩阵对象。

2.6 单日计算函数

开发完最核心的计算函数后，可以自定义一个单日计算函数，计算指定日期的隐含波动率和希腊值，其代码如下：

def calculateOneDayGreek(closPriceWideMatrix, etfPriceWideMatrix, contractInfo, targetDate){
	targetDate_vec = [targetDate]
	r = 0
	optionTodayClose = getTargetDayOptionClose(closPriceWideMatrix, targetDate_vec)
	validContractsToday = optionTodayClose.columnNames()
	etfTodayPrice = getTargetDayEtfPrice(etfPriceWideMatrix, targetDate_vec)
	KPrice, dayRatio, CPMode = getTargetDayContractInfo(contractInfo, validContractsToday, targetDate_vec)
	impvMatrix = calculateImpv(optionTodayClose, etfTodayPrice, KPrice, r, dayRatio, CPMode)
	deltaMatrix = calculateDelta(etfTodayPrice, KPrice, r, dayRatio, impvMatrix, CPMode)\(etfTodayPrice*0.01)
	gammaMatrix = calculateGamma(etfTodayPrice, KPrice, r, dayRatio, impvMatrix)\(pow(etfTodayPrice, 2) * 0.0001)
	vegaMatrix = calculateVega(etfTodayPrice, KPrice, r, dayRatio, impvMatrix)
	thetaMatrix = calculateTheta(etfTodayPrice, KPrice, r, dayRatio, impvMatrix, CPMode)
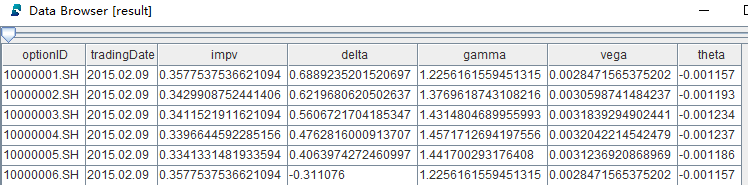
	todayTable = table(validContractsToday as optionID, impvMatrix.reshape() as impv, deltaMatrix.reshape() as delta, gammaMatrix.reshape() as gamma, vegaMatrix.reshape() as vega, thetaMatrix.reshape() as theta)
	todayTable["tradingDate"] = targetDate
	todayTable.reorderColumns!(["optionID", "tradingDate"])
	return todayTable
}

calculateOneDayGreek 的入参 closPriceWideMatrix, etfPriceWideMatrix 是矩阵对象（参考第1章节的读取数据），contractInfo 是表对象（参考第1章节的读取数据），targetDate 是标量对象。

calculateOneDayGreek 函数还调用了 getTargetDayOptionClose 函数， getTargetDayEtfPrice 函数和getTargetDayContractInfo 函数，调用的目的是从全量数据中获取计算当日的有效信息，代码如下：

/*
 * 按合约和交易日在期权日频收盘价矩阵中寻找对应价格
 */
def getTargetDayOptionClose(closPriceWideMatrix, targetDate){
	colNum = closPriceWideMatrix.colNames().find(targetDate)
	return closPriceWideMatrix[colNum].transpose().dropna(byRow = false)
}

/*
 * 按合约和交易日在期权合成期货价格矩阵中寻找对应价格
 */
def getTargetDayEtfPrice(etfPriceWideMatrix, targetDate){
	colNum = etfPriceWideMatrix.colNames().find(targetDate)
	return etfPriceWideMatrix[colNum].transpose().dropna(byRow = false)
}

/*
 * 根据合约和交易日在期权信息表中寻找 KPrice, dayRatio, CPMode
 */
def getTargetDayContractInfo(contractInfo, validContractsToday, targetDate){
	targetContractInfo = select code, exemode, exeprice, lastdate, exeprice2, dividenddate, targetDate[0] as tradingDate from contractInfo where Code in validContractsToday
	KPrice = exec iif(tradingDate<dividenddate, exeprice2, exeprice) from targetContractInfo pivot by tradingDate, code
	dayRatio = exec (lastdate-tradingDate)\365.0 from targetContractInfo pivot by tradingDate, Code
	CPMode = exec exemode from targetContractInfo pivot by tradingDate, Code
	return KPrice, dayRatio, CPMode
}

calculateOneDayGreek 函数的具体使用方法会在下一章说明。

2.7 多日并行计算函数

自定义单日计算函数后，可以再自定义一个多日并行计算函数，其代码如下：

def calculateAll(closPriceWideMatrix, etfPriceWideMatrix, contractInfo, tradingDates, mutable result){
	calculator = partial(calculateOneDayGreek, closPriceWideMatrix, etfPriceWideMatrix, contractInfo)
	timer{
		allResult = ploop(calculator, tradingDates)
	}
	for(oneDayResult in allResult){
		append!(result, oneDayResult)
	}	
}

calculateAll 是自定义的多日并行计算函数，主要用到了 DolphinDB 内置的 partial 部分应用函数和 ploop 并行计算函数，直接传入要并行的函数和入参，不必像其他语言一样先定义线程池/进程池。calculateAll 函数的具体使用方法会在下一章说明。

3. 计算性能测试

测试的交易日范围从2015年2月到2022年3月，实际交易日1729天。测试的期权品种是 50 ETF，证券代码为510050，涉及期权合约共3124个。

3.1 测试环境

  • CPU 类型：Intel(R) Xeon(R) Silver 4216 CPU @ 2.10GHz

  • 逻辑 CPU 总数：8

  • 内存：64GB

  • OS：64位 CentOS Linux 7 (Core)

  • DolphinDB server 版本：2.00.8 JIT

3.2 单日计算性能测试

单线程单日计算性能测试代码如下：

//定义单日性能测试函数
def testOneDayPerformance(closPriceWideMatrix, etfPriceWideMatrix, contractInfo, targetDate){
	targetDate_vec = [targetDate]
	r = 0
	optionTodayClose = getTargetDayOptionClose(closPriceWideMatrix, targetDate_vec)
	validContractsToday = optionTodayClose.columnNames()
	etfTodayPrice = getTargetDayEtfPrice(etfPriceWideMatrix, targetDate_vec)
	KPrice, dayRatio, CPMode = getTargetDayContractInfo(contractInfo, validContractsToday, targetDate_vec)
	timer{
		impvMatrix = calculateImpv(optionTodayClose, etfTodayPrice, KPrice, r, dayRatio, CPMode)
		deltaMatrix = calculateDelta(etfTodayPrice, KPrice, r, dayRatio, impvMatrix, CPMode)\(etfTodayPrice*0.01)
		gammaMatrix = calculateGamma(etfTodayPrice, KPrice, r, dayRatio, impvMatrix)\(pow(etfTodayPrice, 2) * 0.0001)
		vegaMatrix = calculateVega(etfTodayPrice, KPrice, r, dayRatio, impvMatrix)
		thetaMatrix = calculateTheta(etfTodayPrice, KPrice, r, dayRatio, impvMatrix, CPMode)
	}
	todayTable = table(validContractsToday as optionID, impvMatrix.reshape() as impv, deltaMatrix.reshape() as delta, gammaMatrix.reshape() as gamma, vegaMatrix.reshape() as vega, thetaMatrix.reshape() as theta)
	todayTable["tradingDate"] = targetDate
	todayTable.reorderColumns!(["optionID", "tradingDate"])
	return todayTable
}
//执行单日性能测试函数
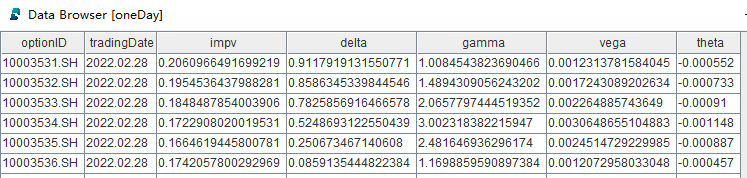
oneDay = testOneDayPerformance(closPriceWideMatrix, etfPriceWideMatrix, contractInfo, 2022.02.28)

测试结果如下：

  • 计算日期为 2022年2月28日

  • 测试的期权品种是 50 ETF，涉及期权合约共136个

  • DolphinDB 脚本计算总耗时为2.1 ms

  • C++ 原生代码计算总耗时为1.02 ms

3.3 多日并行计算性能测试

多日并行计算性能测试代码如下：

//创建存储计算结果的表变量
result = table(
		array(SYMBOL, 0) as optionID,
		array(DATE, 0) as tradingDate,
		array(DOUBLE, 0) as impv,
		array(DOUBLE, 0) as delta,
		array(DOUBLE, 0) as gamma,
		array(DOUBLE, 0) as vega,
		array(DOUBLE, 0) as theta
	)
//执行多日并行计算函数
calculateAll(closPriceWideMatrix, etfPriceWideMatrix, contractInfo, tradingDates, result)

测试结果如下：

  • 计算日期为 2015年2月到2022年3月

  • 测试的期权品种是 50 ETF，涉及期权合约共3124个

  • 计算的并行度为8，测试环境的8个 CPU 满负荷运行

  • DolphinDB 脚本计算总耗时为300 ms

  • C++ 原生代码计算总耗时为200 ms

计算过程中的 CPU 使用率：

4. 总结

本教程中期权隐含波动率的计算使用了 JIT 功能提速，其余希腊值的计算使用了向量化计算。我们测试了2015年2月到2022年3月 50 ETF 所有期权合约的隐含波动率和希腊值的计算性能，在8个 CPU 满负荷运行下，DolphinDB 脚本计算总耗时为300 ms，C++ 原生代码计算总耗时为200 ms，耗时相差50%左右。

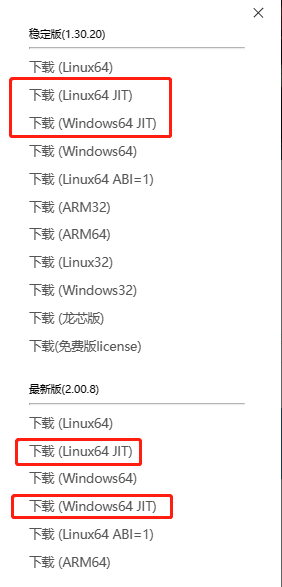
关于 DolphinDB JIT 的更多详细特性，可以参考 DolphinDB JIT教程。

通过 DolphinDB 下载连接下载 DolphinDB server 进行测试的时候，必须选择包含 JIT 功能的安装包，如下图所示：

附录

调用计算函数的计算脚本.txt

期权隐含波动率和希腊值计算函数.txt

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/348604.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

PO模式在Selenium中简单实践

PO模式在Selenium中简单实践

初识PO模式 PO&#xff08;PageObject&#xff09;是一种设计模式。简单来说就是把一些繁琐的定位方法、元素操作方式等封装到类中&#xff0c;通过类与类之间的调用完成特定操作。 PO被认为是自动化测试项目开发实践的最佳设计模式之一。 在学习PO模式前&#xff0c;可以先…
阅读更多...
InstructGPT笔记

InstructGPT笔记

一、InstructGPT是在GPT3上微调&#xff0c;ChatGPT是在GPT3.5上微调 二、该论文展示了怎么样对语言模型和人类意图之间进行匹配&#xff0c;方法是在人类的反馈上进行微调。 **三、方法简介&#xff1a;**收集很多问题&#xff0c;使用标注工具将问题的答案写出来&#xff0…
阅读更多...
大数据面试题flume篇

大数据面试题flume篇

1.Flume 的Source&#xff0c;Sink&#xff0c;Channel 的作用&#xff1f;你们Source 是什么类型&#xff1f; 1. 作用 &#xff08;1&#xff09;Source组件是专门用来收集数据的&#xff0c;可以处理各种类型、各种格式的日志数据&#xff0c;包括 avro、thrift、exec、jm…
阅读更多...
Nginx介绍及安装（windows版，Linux版）

Nginx介绍及安装（windows版，Linux版）

目录 一、Nginx介绍 1、Nginx优势 2、Nginx作用 3、部署静态资源 4、代理 5、负载均衡 二、Nginx安装步骤&#xff08;windows版&#xff09; 三、Nginx安装步骤&#xff08;Linux版&#xff09; 1、官网下载安装包&#xff0c;下载完之后上传到Linux系统上 2、在Lin…
阅读更多...
股票量化策略是如何被执行出来的？

股票量化策略是如何被执行出来的？

在股票量化方面&#xff0c;很多投资者是不知道怎么样挖掘量化策略&#xff0c;便在量化交易接口方面会通过股票交易接口将数据慢慢挖掘出来&#xff0c;就简单的通过api接口调用数据方面&#xff0c;直接通过交易接口端输出交易持仓数据&#xff0c;并且通过交易系统对数据的筛…
阅读更多...
什么是“镜像浏览”？文件夹加密后的镜像浏览有什么用？

什么是“镜像浏览”？文件夹加密后的镜像浏览有什么用？

电脑中的文件夹经常用来储存各种重要文件&#xff0c;加密保护成为很多人的选择&#xff0c;而夏冰加密软件拥有各种适用于不同场景的文件夹加密软件&#xff0c;备受用户喜爱。在我们打开加密文件夹之后&#xff0c;我们可以在加密控制面板中发现“镜像浏览”的按钮&#xff0…
阅读更多...
Sharding-jdbc

Sharding-jdbc

一、概念理解垂直切分&#xff1a;包含垂直分库和垂直分表1.1、垂直分库 &#xff1a;专库专用&#xff08;按照业务类型对表分类&#xff09;1.2、垂直分表&#xff1a;基于数据表的列&#xff08;字段&#xff09;为依据切分的&#xff0c;是一种大表拆小表的模式。1.3、垂直…
阅读更多...
【Python--torch（激活函数说明+代码讲解）】激活函数（sigmoid/softmax/ELU/ReLU/LeakyReLU/Tanh）

【Python--torch（激活函数说明+代码讲解）】激活函数（sigmoid/softmax/ELU/ReLU/LeakyReLU/Tanh）

【Python–torch】激活函数(sigmoid/softmax/ELU/ReLU/LeakyReLU/Tanh) 文章目录【Python--torch】激活函数(sigmoid/softmax/ELU/ReLU/LeakyReLU/Tanh)1. 介绍2. 常用激活函数说明2.1 Sigmoid2.1.1 公式2.1.2 图像2.1.3 代码解读2.2 Softmax2.2.1 公式2.2.2 代码解读2.3 ELU2.…
阅读更多...
荧光探针Pyrene-PEG2-Propargyl,芘甲酰胺-二聚乙二醇-丙炔

荧光探针Pyrene-PEG2-Propargyl,芘甲酰胺-二聚乙二醇-丙炔

Pyrene-PEG2-Propargyl物理参数&#xff1a; CAS号&#xff1a;N/A | 英文名&#xff1a;Pyrene-PEG2-Propargyl |中文名&#xff1a;芘甲酰胺-二聚乙二醇-丙炔分子式&#xff1a;C24H21NO3分子量&#xff1a;371.44纯度标准&#xff1a;95%外形颜色&#xff1a;淡黄色或白色固…
阅读更多...
shell学习4

shell学习4

目录 一、统计文本中的词频 二、压缩javascript 三、打印文件的或行中的第n个单词或列---awk 3.1 利用awk打印文件中每行中的第五个单词。 3.2 利用awk打印当前目录下的文件的权限和文件名 3.3 利用awk打印从M行到N行这个范围内的所有文本 3.4 利用awk 部分提取文件中的内…
阅读更多...
opencv复习

opencv复习

文章目录图像衡量结果&#xff08;损失函数&#xff09;预测的好坏前向传播 反向传播图像 实质是矩阵 长 宽 像素通道&#xff08;0-255 0 黑 255 亮&#xff09; 假设这里做一个10分类 行向量✖列向量是一个数 分类 最后的结果是一个各个分类的概率值 这里的b是偏置项&…
阅读更多...
学校节能降耗减排方案——能耗监管平台的建设及效果剖析

学校节能降耗减排方案——能耗监管平台的建设及效果剖析

摘要&#xff1a;作为崭新的校园能耗管理手段&#xff0c;能耗监测平台以传统管理方式无法企及的优势有力地提升了高校能源管理工作的水平&#xff0e;从而受到了相关管理者的青睐。本文梳理总结了高校能耗监测平台的基本组成和优势特点&#xff0c;同时对能耗平台建设和使用中…
阅读更多...
nginx设置重定向跳转后ip:[端口]/abc变成ip/abc而报错404

nginx设置重定向跳转后ip:[端口]/abc变成ip/abc而报错404

nginx设置重定向跳转后 ip:[端口]/abc 变成 ip/abc 而报错404nginx配置&#xff1a;server {listen 80;server_name _;client_max_body_size 300m;absolute_redirect off;location / {root html;index index.html index.htm;proxy_set_header X-Real-IP $remote_a…
阅读更多...
【nodejs-04】黑马nodejs学习笔记04-MySQL简介及安装

【nodejs-04】黑马nodejs学习笔记04-MySQL简介及安装

文章目录1.数据库的基本概念1.1什么是数据库1.2 常见的数据库及分类1.3 传统型数据库的数据组织结构2.安装并配置MySQL2.1 了解需要安装哪些MySQL相关的软件2.2 MySQL 在 Mac 环境下的安装2.3 MySQL 在 Windows 环境下的安装1.数据库的基本概念 1.1什么是数据库 数据库&#x…
阅读更多...
JavaWeb学习

JavaWeb学习

文章目录Tomcat 详解1 Tomcat 安装2 默认端口号3 面试题4 编写与发布一个网站Http 详解1 http 请求2 http 响应3 面试题Tomcat 详解 1 Tomcat 安装 进入Tomcat官网下载压缩包&#xff1a;https://tomcat.apache.org/ 将压缩包解压即可直接使用 启动Tomcat:bin目录下startup.b…
阅读更多...
【软件测试】如何在测试团队中工作游刃有余？你的测试技巧......

【软件测试】如何在测试团队中工作游刃有余？你的测试技巧......

目录&#xff1a;导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结&#xff08;尾部小惊喜&#xff09;前言 在测试团队中&#…
阅读更多...
基于数据库实现分布式锁

基于数据库实现分布式锁

分布式锁概述 前言 我们的系统都是分布式部署的&#xff0c;日常开发中&#xff0c;秒杀下单、抢购商品等等业务场景&#xff0c;为了防⽌库存超卖&#xff0c;都需要用到分布式锁。 分布式锁其实就是&#xff0c;控制分布式系统不同进程共同访问共享资源的一种锁的实现。如…
阅读更多...
xshell6运行报错：由于找不到mfc110u.dll、MSVCR110.dll无法继续执行代码

xshell6运行报错：由于找不到mfc110u.dll、MSVCR110.dll无法继续执行代码

今天给大家分享一下我刚装完系统遇到得问题，由于新盟的罗建雨【胡巴】老师帮我给电脑加了固态，又重装了系统，因此电脑里面得所有软件需要重装，在我重装的过程中遇到了一个小问题给大家分享一下，如果大家以后遇到也方便解决。 问题： 安装Xshell时电脑系统报错：“由于找…
阅读更多...
一、微服务架构介绍

一、微服务架构介绍

目录 一、微服务架构介绍 二、出现和发展 三、传统开发模式和微服务的区别 四、微服务的具体特征 五、SOA和微服务的区别 1、SOA喜欢重用&#xff0c;微服务喜欢重写 2、SOA喜欢水平服务&#xff0c;微服务喜欢垂直服务 3、SOA喜欢自上而下&#xff0c;微服务喜欢自下…
阅读更多...
为什么项目的时间跟踪管理很重要 ?

为什么项目的时间跟踪管理很重要 ?

项目通常被分解为需要完成的任务&#xff0c;以实现项目目标。时间跟踪可以帮助你了解每项任务需要多长时间&#xff0c;从而使你更准确地估计未来的项目。 除此以外&#xff0c;跟踪项目时间还有以下令人难以置信的好处&#xff1a; 1、提高生产力 通过记录在每项任务上花…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023