题目链接：https://leetcode.cn/problems/check-if-it-is-a-good-array/description/

思路

方法：数论

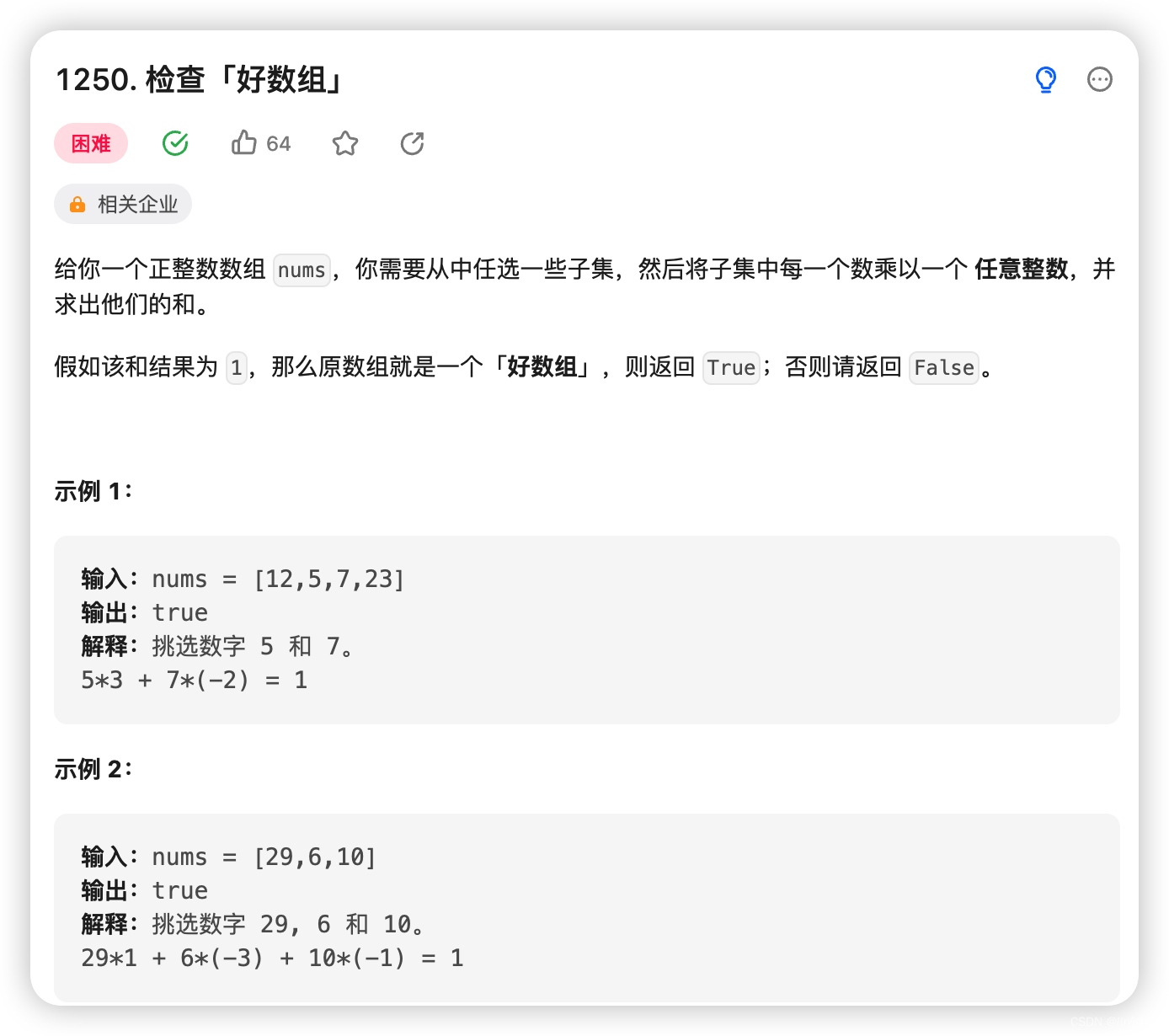
题目意思很简单，让你在数组 nums中选取一些子集，可以不连续，子集中的每个数再乘以任意的数的和是否为1，是则原数组就是个「好数组」

关键词：每个数相乘任意一个数相加，数论里「裴蜀定理」是一个关于最大公约数的定理。也是拥有类似的推导（具体证明可参考「裴蜀定理」OI Wiki）。

「裴(pei)蜀定理」：设 a,b 是不全为零的整数，则存在整数 x,y, 使得 ax+by= gcd(a,b).

「裴蜀定理」同样也可以推广到多个整数的情况。对于全不为 0 的任意 n 个整数 a₁, a₂, a₃, a₄ … a_n，记这 n 个整数的最大公约数为 0，则对于任意 n 个整数 x₁, x₂, x₃, x₄ … x_n都满足 ${\sum }_{i=1}^n{a}_i\ast x_i$ 是 g 的倍数。

推论：正整数 a₁ 到 a_n 的最大公约数是 1 的充分必要条件是存在 n 个整数 x₁ 到 x_n 满足 ${\sum }_{i=1}^n{a}_i\ast x_i=1$

回到原题，我们判断数组 nums 是否是个「好数组」。由「裴蜀定理」推导 0 < i < n，题目等价于求 nums 中的全部数字的最大公约数是否等于 1，若等于 1 则原数组为「好数组」，否则不是。

如何求数组 nums 的 最大公约数 g，初始化 g = nums[0]，遍历数组，更新 g = gcd(g, nums[i])，遍历完全部数字后，g 即为数组 nums 中全部的元素的最大公约数。然后判断其是否等于 1 即可。在实现过程中我们也可以进一步做优化：如果遍历过程中出现最大公约数等于 1 的情况，则由于 1 和任何正整数的最大公约数都是 1，此时可以提前结束遍历。

代码示例

func isGoodArray(nums []int) bool {
	// 有数据为[1]的情况
    if len(nums) == 1 && nums[0] == 1{
        return true
    }
    g := nums[0]
    for i := 1; i < len(nums); i++ {
        g = gcd(g, nums[i])
        if g == 1 {
            return true
        }
    }
    return false
}

func gcd(a, b int) int {
    if a % b == 0 {
        return b
    }
    return gcd(b, a % b)
}

复杂度分析

• 时间复杂度：O(n + $\log m$)，其中n表示数组 nums 长度，m 表示与最大公约数 g 迭代次数最长的数字，其中求单次最大公约数的时间复杂度为 O($\log m$)，两个数求最大公约数，其中最大公约数 g 自增不减，总的求最大公约数所需时间为O($\log m$)，所以总的所需时间O(n + $\log m$)
• 空间复杂度：O(1)，不需要额外申请空间