电子技术——多阶放大器

实际上的商用放大器是由多个单阶放大器联级而成的多阶放大器。首先第一阶（输入）通常提供一个较大的输出阻抗来保证较小的信号衰减。若是差分放大器，还要保证有较大的共模抑制比。中间各阶放大器负责提供电压增益，有时还提供差分到单端转换的功能。或是移动DC分量使得信号可以正负回摆。

最后，最后一阶（输出）放大器主要是提高一个较小的输出阻抗来保证较小的信号衰减。并且，最后一阶放大器还需要保证能提供需要的电流，来保证较大的输出功率，也就是说最后一阶放大器不应该损失较大的功率。我们已经学习过了一种输出放大器——源极（射极）跟随器，但是以后的章节我们会学习到源极（射极）跟随器具有较大的功率损失，以后的章节我们会学习更好的解决方案。

为了说明多阶放大器结构，我们将会举两个例子来说明：一个两阶的CMOS运算放大器和一个四阶的BJT运算放大器。

两阶的CMOS运算放大器

下图展示了一个两阶的CMOS运算放大器：

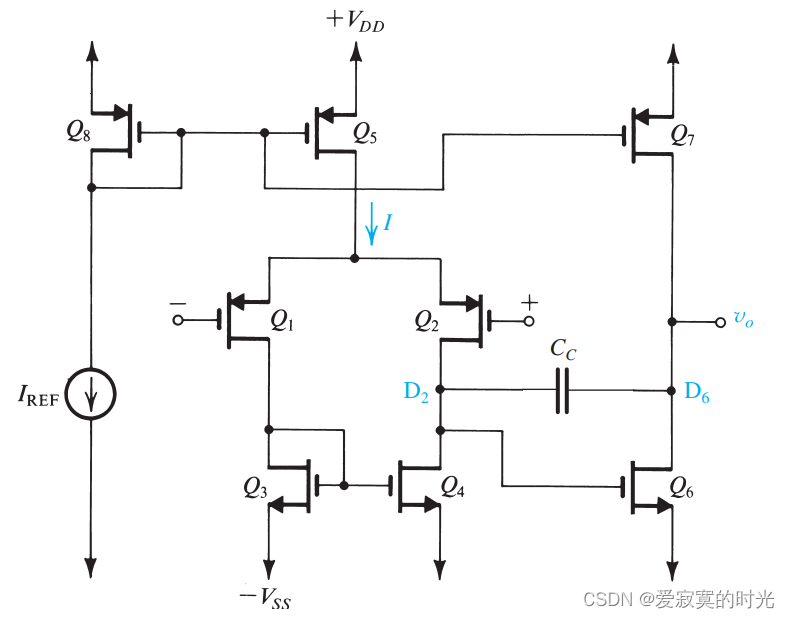
该运算放大器使用双电源方案，对于 $0.5\mu m$工艺可以使用 $\pm 2.5V$ 电源，而对于 $65nm$ 工艺降低至 $\pm 0.5V$ 。参考电流 $I_{REF}$ 由片外电路生成或是通过片内电路生成。参考电流生成电路会在以后的章节讨论。电流镜输出 $Q_5$ 为差分对 $Q_1$ 和 $Q_2$ 提供电流偏置。差分对使用电流镜 $Q_3$ 和 $Q_4$ 负载。

第二阶是 $Q_6$ 组成了一个共源极放大器，其中 $Q_7$ 作为主动负载。电容 $C_c$ 作为负反馈回路，我们将在以后学习。

上述方案一个严重的缺点是缺失低阻抗的输出阶，实际上的输出阻抗为 $(r_{o6}||r_{o7})$ 仍然很高。因此这个电路不适合低阻抗负载。尽管如此，该电路在VLSI设计上仍很受欢迎，特别是在驱动小容抗负载，例如我们之后要学习的开关电容电路。这个电路的优点是简单，可以在较小的IC区域中实现一个简单的运算放大器。

电压增益

我们已经计算过，第一阶的电压增益为：

$$A_1=-g_{m1}(r_{o2}||r_{o4})$$

第二阶是一个共源极放大器，其增益为：

$$A_2=-g_{m6}(r_{o6}||r_{o7})$$

则总开路增益为：

$$A_{vo}=A_1{A}_2=g_{m1}(r_{o2}||r_{o4})g_{m6}(r_{o6}||r_{o7})$$

输入偏移电压

电路任何时候都不是完美匹配的，因此存在输入偏移电压。因为电路的非理想因素是随机的，我们无法提前预知，这种输入偏移电压称为 随机偏移 。而对于即使电路不存在非理想，即电路是完美匹配的，此时的输入偏移电压称为 系统偏移 。系统偏移可以通过精心设计电路以降低至最小。

为了计算上述电路的系统偏移，我们将两个输入端置地。如果输入阶是完美平衡的，那么 $Q_4$ 的漏极电压应该为 $-V_{SS}+V_{GS4}$ ，因此 $Q_6$ 的 $V_{GS6}=V_{GS4}$ 。所以有：

$$I_6=\frac{(W/L{)}_6}{(W/L{)}_4}(I/2)$$

若想无偏移电压，那么必须保证此时 $Q_6$ 的电流等于 $Q_7$ 的电流，此时：

$$I_7=\frac{(W/L{)}_7}{(W/L{)}_5}I$$

现在：

$$\frac{(W/L{)}_6}{(W/L{)}_4}=2\frac{(W/L{)}_7}{(W/L{)}_5}$$

若上述条件满足，则无系统偏移。

四阶的BJT运算放大器

我们第二个例子是四阶的BJT运算放大器，如图所示：

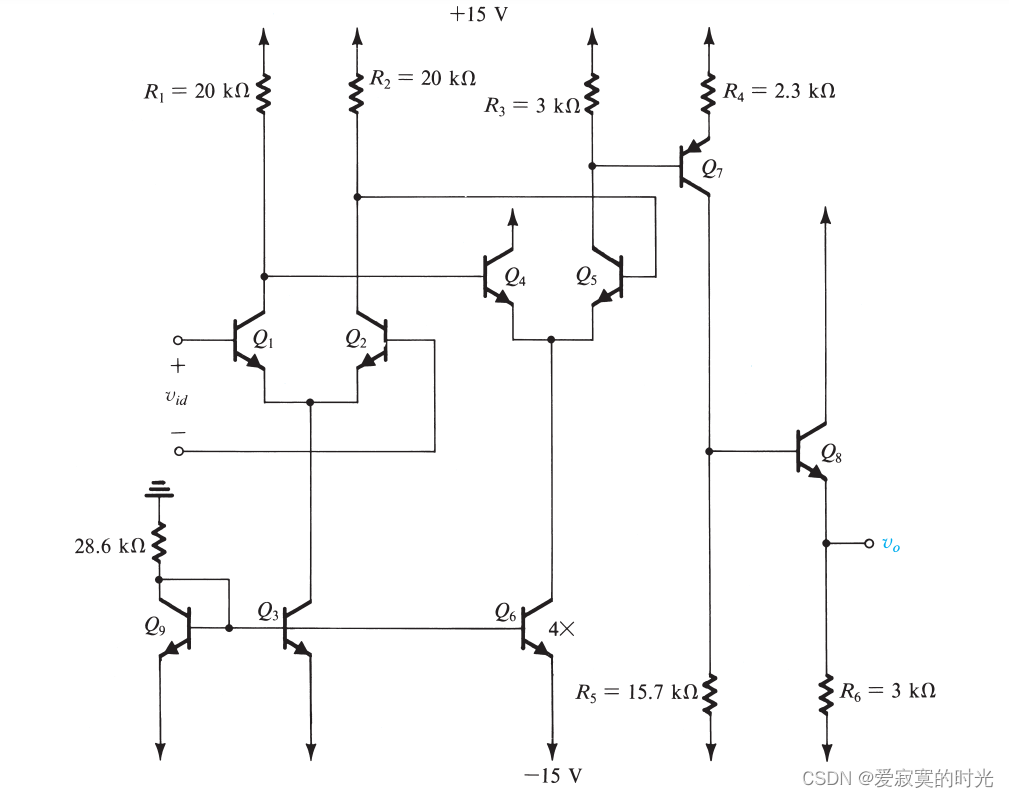
这个运算放大器由四阶组成，第一阶是差分输入，差分输出的 $Q_1$ 和 $Q_2$ 组成，通过电流镜 $Q_3$ 偏置。第二阶是差分输入，单端输出的 $Q_4$ 和 $Q_5$ ，通过 $Q_6$ 偏置。

为了提供更大的增益，第三阶 $Q_7$ 提供了移动DC分量的功能。因为 $Q_5$ 的集电极电压不可以低于基极电压（10V），但是通过PNP $Q_7$ 的转换， $Q_7$ 的集电极电压可以低于10V，将其DC分量下移，允许信号正负回摆。最后一阶是射极跟随器，提供较大的输出阻抗。

电流增益分析

存在一种更为简单的方法分析BJT放大器电路，使用电流增益或电流传导系数。下图是一个我们准备好的电路，我们只分析其中的小信号，如图：

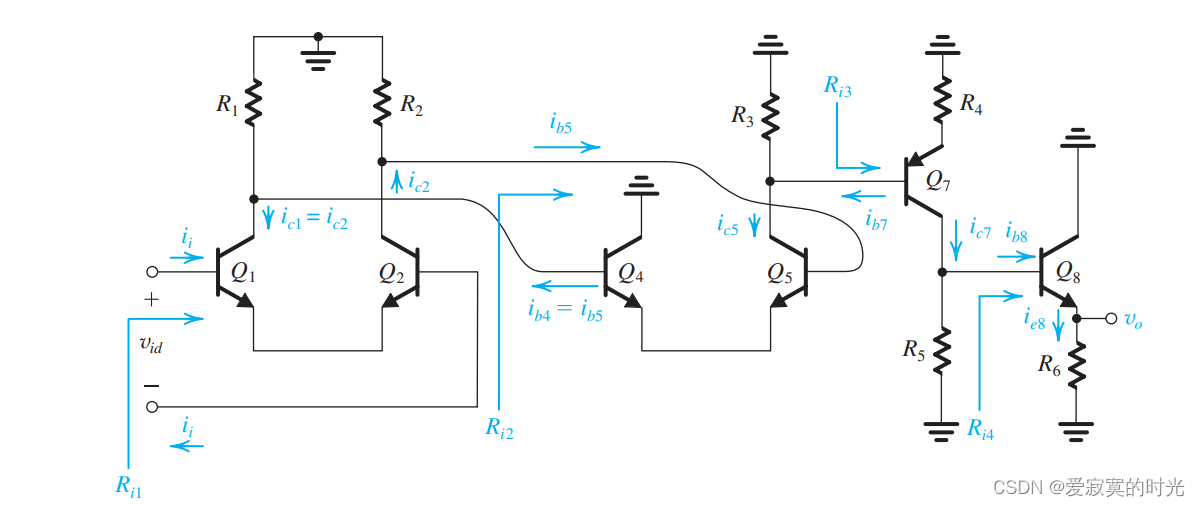
所有的支路电流我们都已经标出来了。目标是计算总的电压增益 $v_o/v_{id}$ ，我们从尾部向头部推进：

$$v_o=R_6{i}_{e8}$$

$$v_{id}=R_{i1}{i}_i$$

因此电压增益为：

$$\frac{v_o}{v_{id}}=\frac{R_6}{R_{i1}}\frac{i_{e8}}{i_i}$$

接下来我们将电流增益展开为：

$$\frac{i_{e8}}{i_i}=\frac{i_{e8}}{i_{b8}}\times \frac{i_{b8}}{i_{c7}}\times \frac{i_{c7}}{i_{b7}}\times \frac{i_{b7}}{i_{c5}}\times \frac{i_{c5}}{i_{b5}}\times \frac{i_{b5}}{i_{c2}}\times \frac{i_{c2}}{i_i}$$

右边的电流比要么是BJT的电流比，要么是电阻分流比，我们可以简单计算得到：

$$\frac{i_{e8}}{i_{b8}}={\beta }_8+1$$

$$\frac{i_{b8}}{i_{c7}}=\frac{R_5}{R_5+R_{i4}}$$

$$\frac{i_{c7}}{i_{b7}}={\beta }_7$$

$$\frac{i_{b7}}{i_{c5}}=\frac{R_3}{R_3+R_{i3}}$$

$$\frac{i_{c5}}{i_{b5}}={\beta }_5$$

$$\frac{i_{b5}}{i_{c2}}=\frac{(R_1+R_2)}{(R_1+R_2)+R_{i2}}$$

$$\frac{i_{c2}}{i_i}={\beta }_2$$

乘积就是整体电压增益。