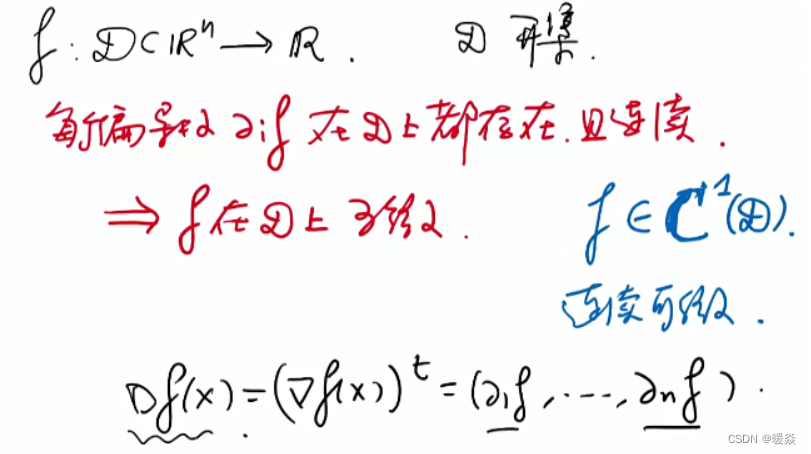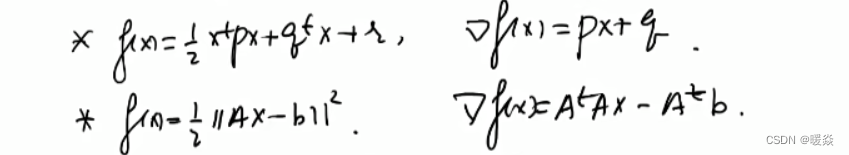高数
- 问题解决流程
- 引例:回归
- 回归
- 引例:分类
- 分类
- 线性可分
- FLD
- 线性不可分
- 智能计算讨论范围
- 下降法
- 为什么要用下降法?- 解析解很难写出公式或很复杂难计算
- 有哪些常用的下降法?- 梯度下降&高斯-牛顿法
- 梯度下降(Gradient Descent)- 本质:一阶泰勒展开式近似
- 如何找到一阶泰勒展开式的最优解(最小值)?- 柯西一施瓦兹不等式
- 结论:下降最快的方向为梯度的反方向,即梯度下降。
- 牛顿法 - 本质:二阶泰勒展开式近似
- 如何找到二阶泰勒展开式的最优解(最小值)?- 梯度=0
- 分类&回归
- 线性分析
- 常用不等式
- 绝对值不等式
- 柯西不等式
- 算术-几何平均不等式
- 数列极限
- 序列极限
- 上极限
- 下极限
- 级数
- 点集拓扑
- 开集
- 开集性质
- 闭集
- 闭集性质
- 紧集
- Heine-Borel定理
- 例题:判断 R n \mathbb{R^n} Rn和 ∅ \emptyset ∅是否开闭紧?
- 函数连续性
- 函数连续定义
- Lipshitz函数是连续函数
- Lipshitz函数与机器学习
- 连续函数逼近
- 拉格朗日插值定理
- 连续函数性质
- 最值定理
- 介值定理
- 不连续函数
- 导数
- 一元函数导数
- 定义
- 意义
- 性质
- 极值定理
- 微分中值定理
- 洛必达法则
- 常用公式
- C ∞ C^\infty C∞
- 多元多值函数
- 可微
- 梯度存在
问题解决流程
idea - math - optimization - algorithm
引例:回归

question:123456x,预测x值为多少?
idea:
f
(
x
i
)
=
a
t
x
i
+
b
,
f
(
x
i
)
≈
y
i
f(x_i)=a^tx_i+b, f(x_i)\approx y_i
f(xi)=atxi+b,f(xi)≈yi,使用
f
(
x
)
f(x)
f(x)预测新样本
x
x
x。
optimization:使用L1、L2范数度量
f
(
x
i
)
f(x_i)
f(xi)和
y
i
y_i
yi的差距,即loss function。如何求出参数使得loss function最小?- 偏导数为0。
algorithm:GD、Newton’s method
回归
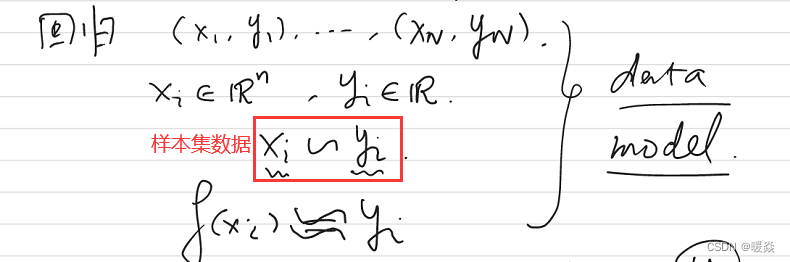



引例:分类
分类
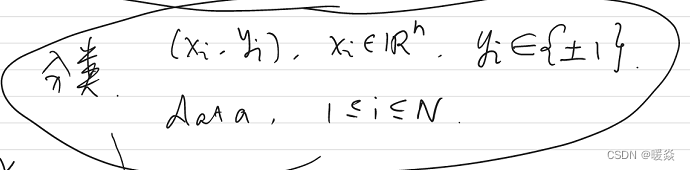
线性可分

FLD

FLD思想:同类点近,不同点远。
根据这个思想,实际的做法是找一条直线,其方向为 ω \omega ω,对线性可分的点进行投影,在该直线上,同类点的投影点更近,异类点的投影点更远。进而做一条垂直于该直线的分类线。
先找到投影λ与xi的关系,然后利用w与v垂直内积为0,求出投影λ的表达式,

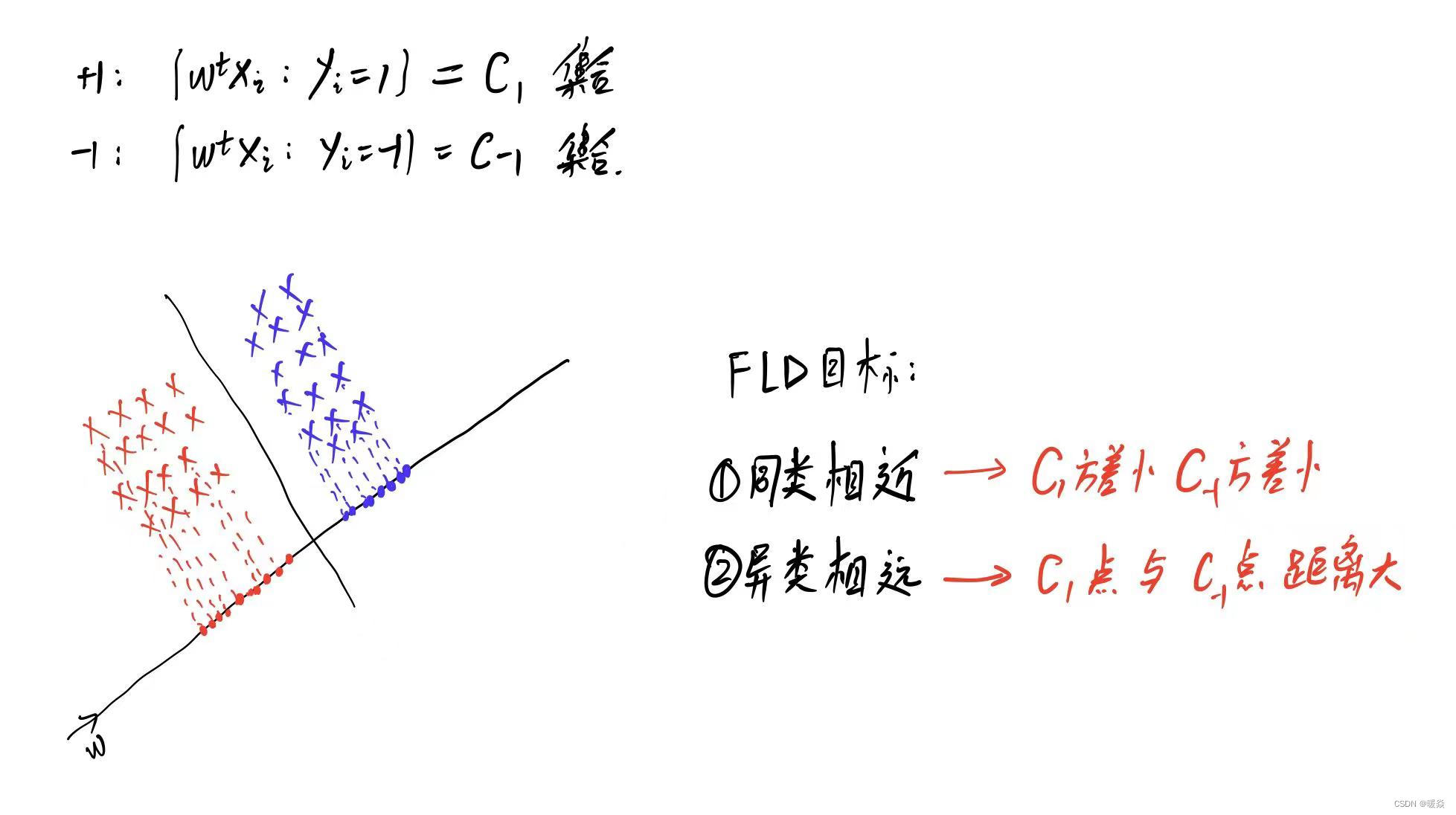

同类相近:要使得C1方差小和C-1的方差小,则将两个优化问题合并为一个优化问题。
异类相远:没有办法计算所有点,所以选择代表性的均值的距离作为两个集合的距离。
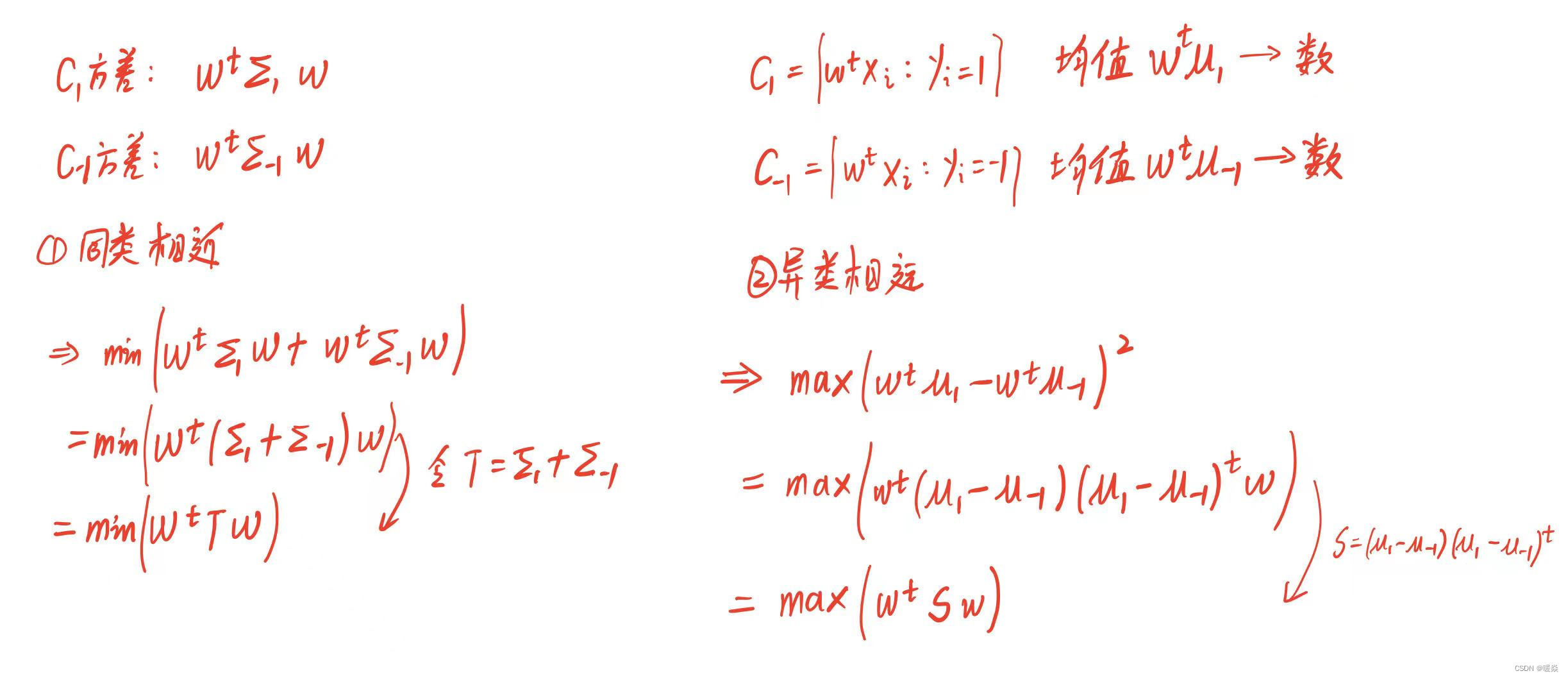
再次将两个优化目标合并为一个单优化目标进行优化。
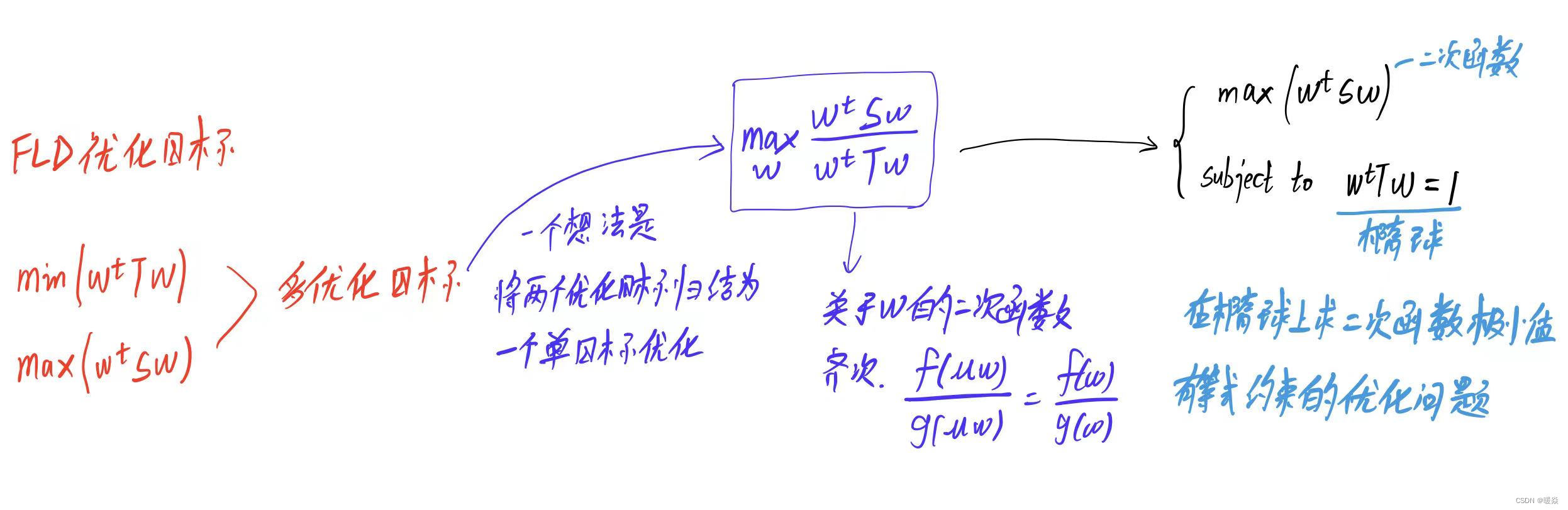
线性不可分
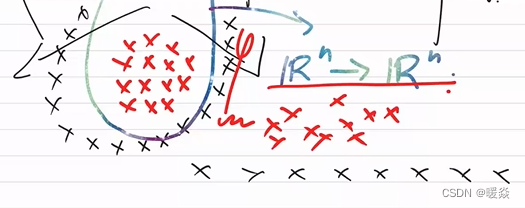
智能计算讨论范围
智能计算讨论的是问题解决流程中的math和optimization。

下降法
为什么要用下降法?- 解析解很难写出公式或很复杂难计算
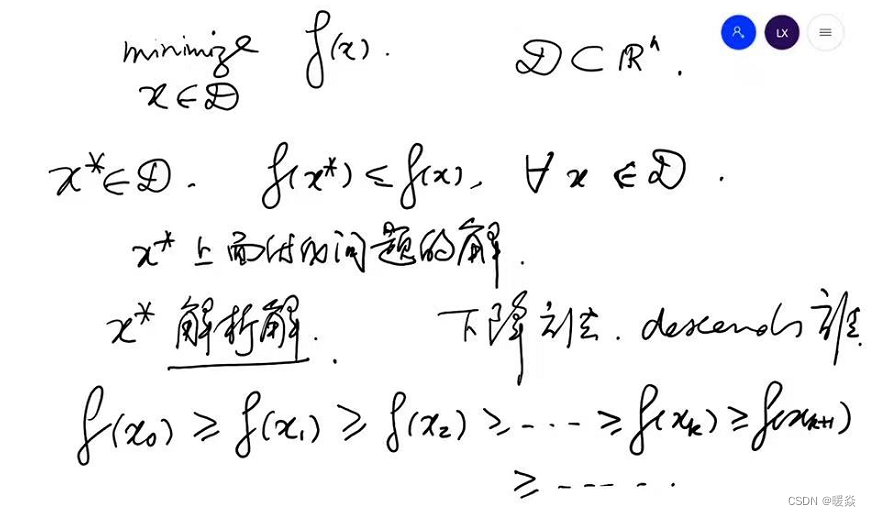
考虑求极值问题场景,需要找到一个 x ∗ x^* x∗使得 f ( x ∗ ) f(x^*) f(x∗)小于等于邻域内的任意 f ( x ) f(x) f(x), x ∗ x^* x∗是极小值问题的解,因为 x ∗ x^* x∗的解析解很难写出公式或者可以写出但是公式很复杂难计算,所以考虑使用下降法。
解析解:指通过严格的公式所求得的解。即包含分式、三角函数、指数、对数甚至无限级数等基本函数的解的形式。给出解的具体函数形式,从解的表达式中就可以算出任何对应值。解析解为一封闭形式的函数,因此对任一独立变量,皆可将其代入解析函数求得正确的相依变量。因此,解析解也称为闭式解。
解析法:用来求得解析解的方法称为解析法,解析法是常见的微积分技巧,如分离变量法等。
下降法亦称极小化方法,是一类重要的迭代法。这类方法将方程组求解问题转化为求泛函极小问题。
使用下降法,找出一系列函数值递减的 f ( x ) f(x) f(x)序列,这个下降过程不是一直持续下去的过程,根据一些停止条件得到一个 x k x_k xk时,这个 x k x_k xk即优化问题的解 x ∗ x^* x∗。
有哪些常用的下降法?- 梯度下降&高斯-牛顿法
梯度下降(Gradient Descent)- 本质:一阶泰勒展开式近似
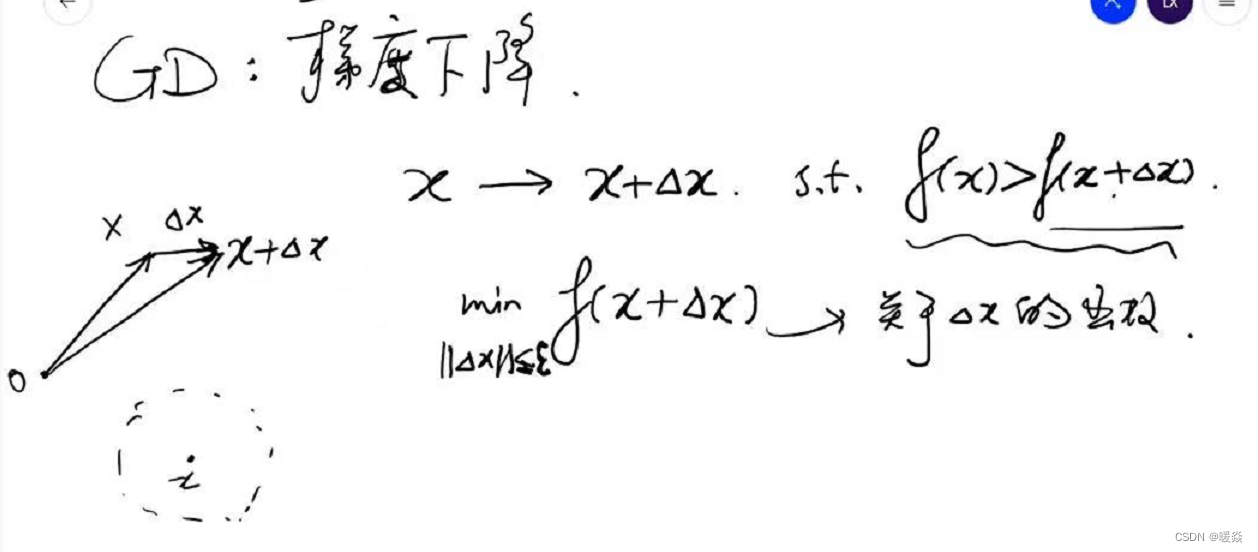
优化问题:在 x x x的邻域内,找到一个 x + Δ x x+ \Delta x x+Δx,使得 f ( x ) > f ( x + Δ x ) f(x)\gt f(x+\Delta x) f(x)>f(x+Δx),且 f ( x + Δ x ) f(x+\Delta x) f(x+Δx)在该邻域最小。
数学问题:如何找到该邻域最小 f ( x + Δ x ) f(x+\Delta x) f(x+Δx)?
问题难点:因为 f ( x ) f(x) f(x)优化问题的解析解不容易求解,因此 f ( x + Δ x ) f(x+\Delta x) f(x+Δx)优化问题的解析解也不容易求解。
解决方法:考虑 f ( x + Δ x ) f(x+\Delta x) f(x+Δx)的线性近似——一阶泰勒展开式。将 m i n ∣ ∣ Δ x ∣ ∣ ≤ ε f ( x + Δ x ) \underset {||\Delta x||\le \varepsilon}{min} f(x+\Delta x) ∣∣Δx∣∣≤εminf(x+Δx)问题转换为 m i n ∣ ∣ Δ x ∣ ∣ ≤ ε ( f ( x ) + a t Δ x ) \underset {||\Delta x||\le \varepsilon}{min} (f(x)+a^t \Delta x) ∣∣Δx∣∣≤εmin(f(x)+atΔx),因为 m i n ∣ ∣ Δ x ∣ ∣ ≤ ε ( f ( x ) + a t Δ x ) \underset {||\Delta x||\le \varepsilon}{min} (f(x)+a^t \Delta x) ∣∣Δx∣∣≤εmin(f(x)+atΔx)中 f ( x ) f(x) f(x)是固定的, Δ x \Delta x Δx是变量,所以问题可再次简化为 m i n ∣ ∣ Δ x ∣ ∣ ≤ ε a t Δ x \underset {||\Delta x||\le \varepsilon}{min} a^t \Delta x ∣∣Δx∣∣≤εminatΔx。
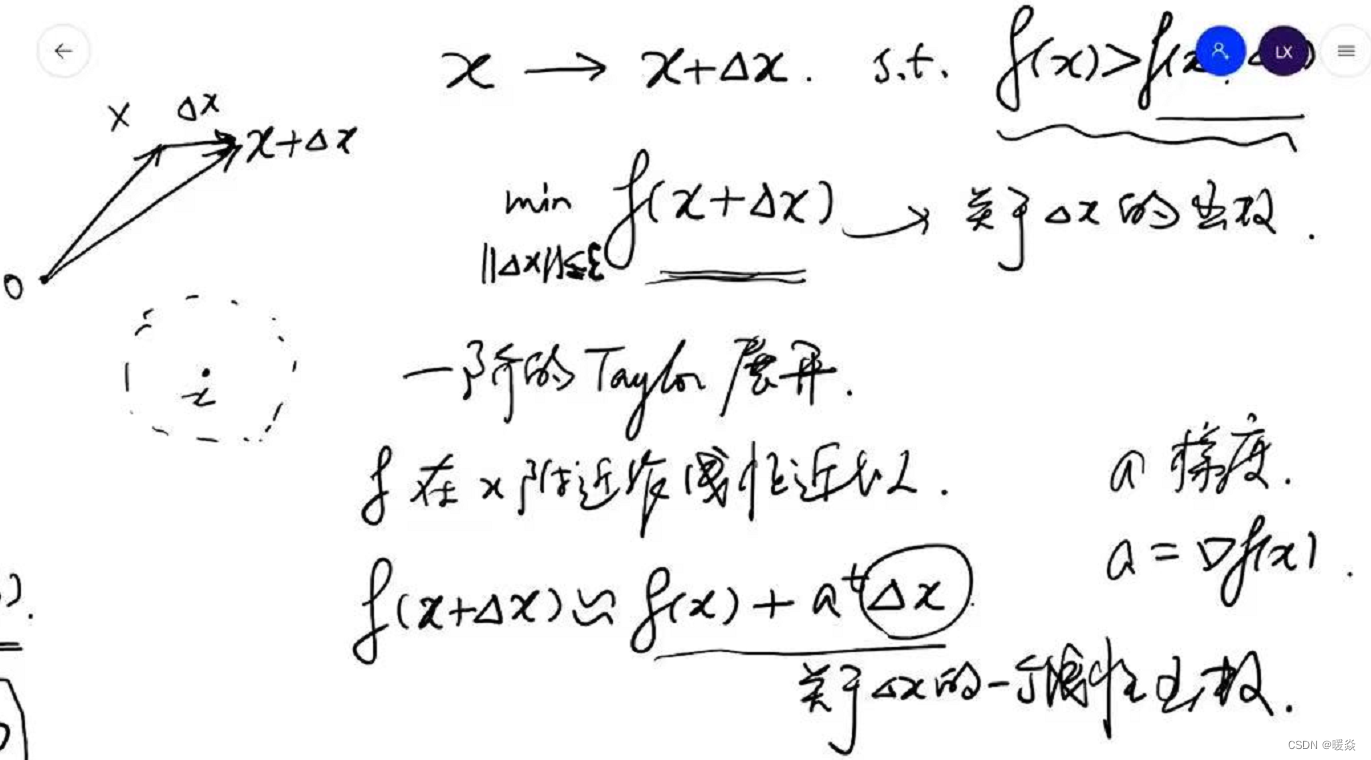
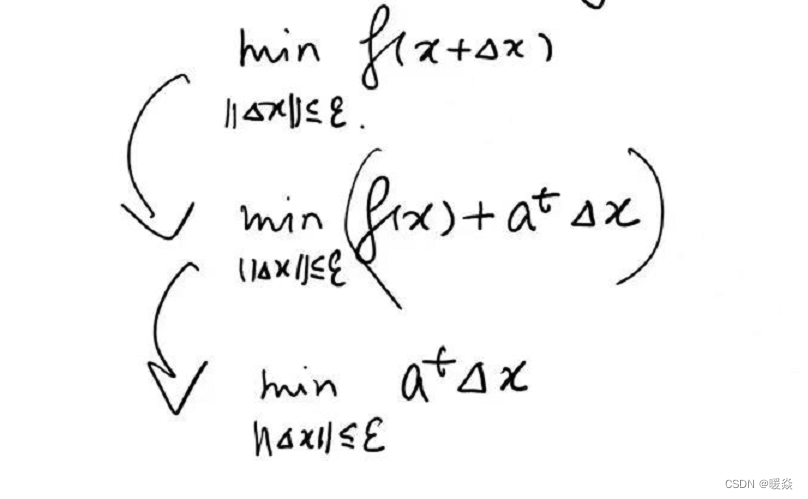
如何找到一阶泰勒展开式的最优解(最小值)?- 柯西一施瓦兹不等式
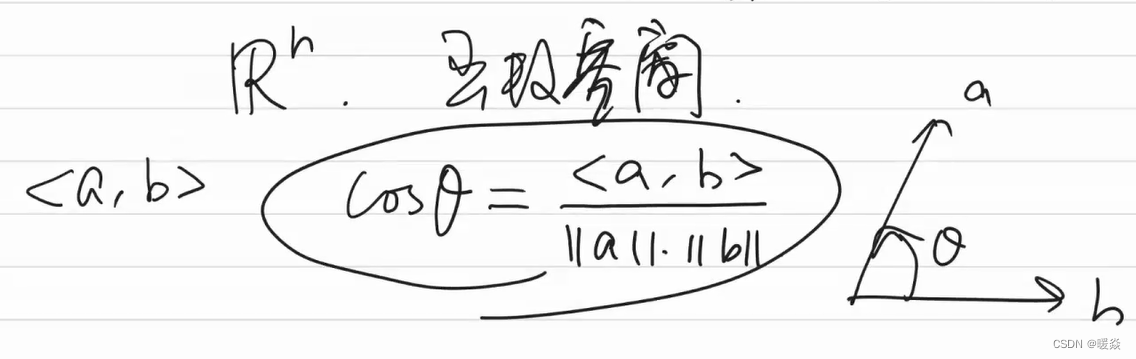
根据柯西一施瓦兹不等式(Cauchy-Schwarz inequality), a t Δ x a^t \Delta x atΔx 的最小值是显而易见的。
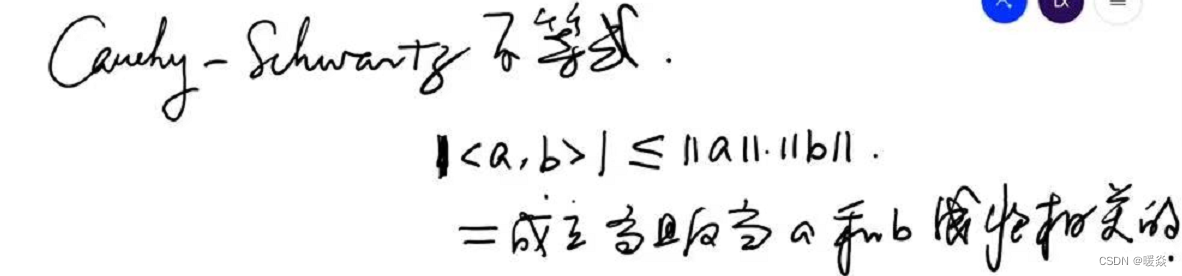
由以上不等式可得:
−
∣
∣
a
∣
∣
⋅
∣
∣
b
∣
∣
≤
<
a
,
b
>
≤
∣
∣
a
∣
∣
⋅
∣
∣
b
∣
∣
-||a||·||b|| \le <a,b> \le ||a||·||b||
−∣∣a∣∣⋅∣∣b∣∣≤<a,b>≤∣∣a∣∣⋅∣∣b∣∣。
当且仅当a和b共线同向时,a和b线性正相关,
<
a
,
b
>
≤
∣
∣
a
∣
∣
⋅
∣
∣
b
∣
∣
<a,b> \le ||a||·||b||
<a,b>≤∣∣a∣∣⋅∣∣b∣∣成立。
当且仅当a和b共线反向时,a和b线性负相关,
−
∣
∣
a
∣
∣
⋅
∣
∣
b
∣
∣
≤
<
a
,
b
>
-||a||·||b|| \le <a,b>
−∣∣a∣∣⋅∣∣b∣∣≤<a,b>成立。
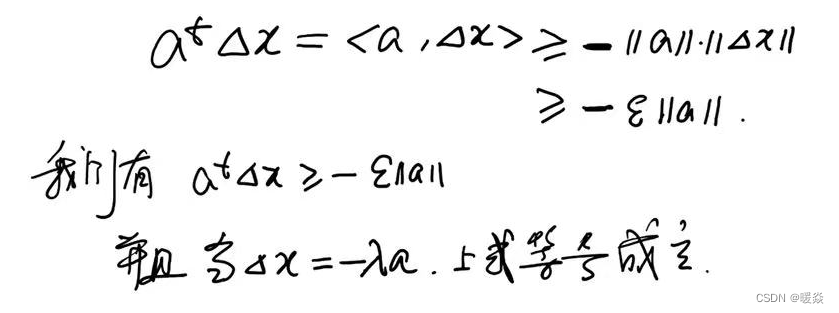
当 Δ x = − λ a \Delta x=-\lambda a Δx=−λa时,表示 Δ x \Delta x Δx与 a a a线性负相关,共线反向, a t Δ x = − ε ∣ ∣ a ∣ ∣ a^t \Delta x=-\varepsilon ||a|| atΔx=−ε∣∣a∣∣成立。
一阶泰勒展开式中,a表示梯度,所以下降最快的方向为梯度的反方向。
结论:下降最快的方向为梯度的反方向,即梯度下降。
λ \lambda λ即为学习率。
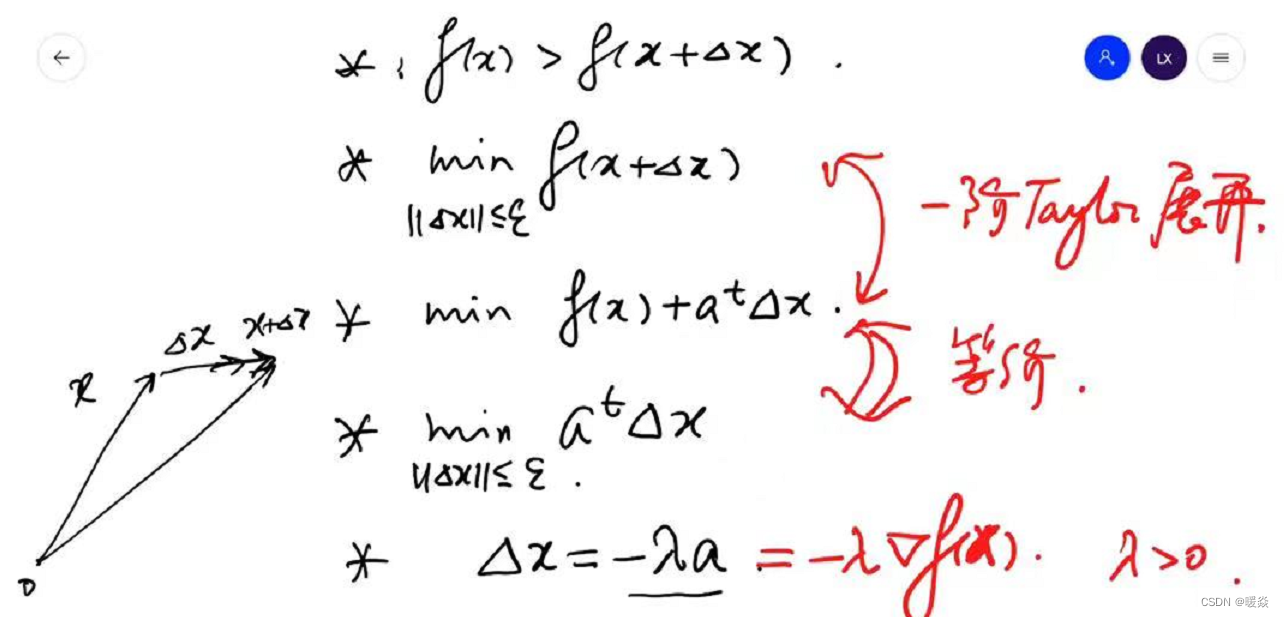
牛顿法 - 本质:二阶泰勒展开式近似
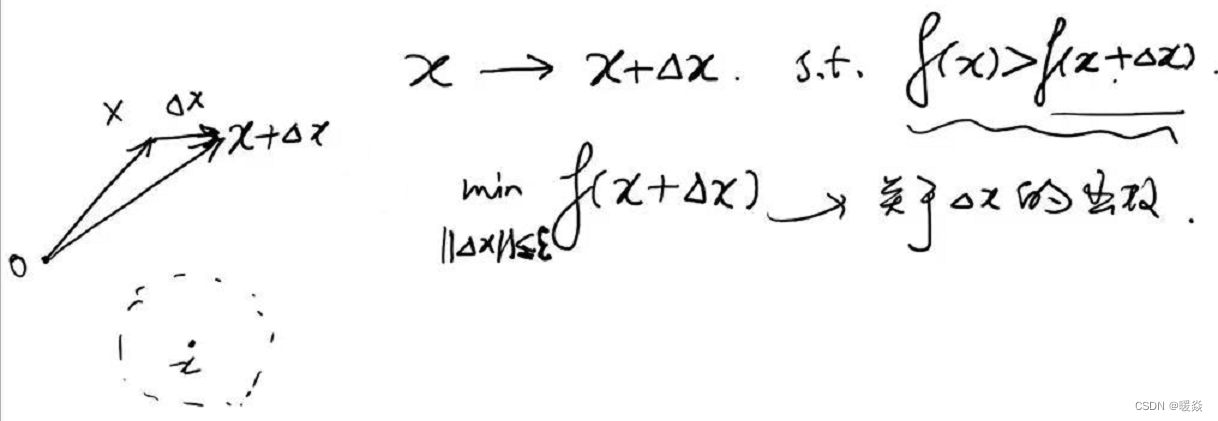
优化问题:在 x x x的邻域内,找到一个 x + Δ x x+ \Delta x x+Δx,使得 f ( x ) > f ( x + Δ x ) f(x)\gt f(x+\Delta x) f(x)>f(x+Δx),且 f ( x + Δ x ) f(x+\Delta x) f(x+Δx)在该邻域最小。
数学问题:如何找到该邻域最小 f ( x + Δ x ) f(x+\Delta x) f(x+Δx)?
问题难点:因为 f ( x ) f(x) f(x)优化问题的解析解不容易求解,因此 f ( x + Δ x ) f(x+\Delta x) f(x+Δx)优化问题的解析解也不容易求解。
解决方法:考虑 f ( x + Δ x ) f(x+\Delta x) f(x+Δx)的线性近似——二阶泰勒展开式。将 m i n ∣ ∣ Δ x ∣ ∣ ≤ ε f ( x + Δ x ) \underset {||\Delta x||\le \varepsilon}{min} f(x+\Delta x) ∣∣Δx∣∣≤εminf(x+Δx)问题转换为 m i n Δ x ( f ( x ) + a t Δ x + 1 2 ( Δ x ) t P Δ x ) \underset {\Delta x}{min} (f(x)+a^t \Delta x+\frac 1 2 (\Delta x)^t P \Delta x) Δxmin(f(x)+atΔx+21(Δx)tPΔx),其中 f ( x ) f(x) f(x)是固定的, Δ x \Delta x Δx是变量, a t Δ x a^t \Delta x atΔx是关于 Δ x \Delta x Δx一次函数, 1 2 ( Δ x ) t P Δ x ) \frac 1 2 (\Delta x)^t P \Delta x) 21(Δx)tPΔx)是 Δ x \Delta x Δx二次函数。
因为使用二阶泰勒展开式近似, f ( x + Δ x ) f(x+\Delta x) f(x+Δx)可看做一个二次函数,可以找到全局最优值,而不需要在邻域中讨论,所以可以删除 ∣ ∣ Δ x ∣ ∣ ≤ ε ||\Delta x||\le \varepsilon ∣∣Δx∣∣≤ε条件。
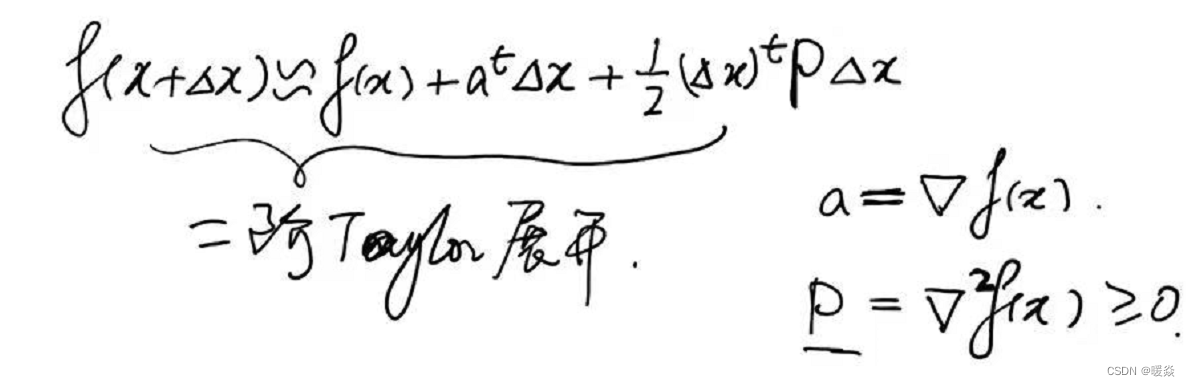
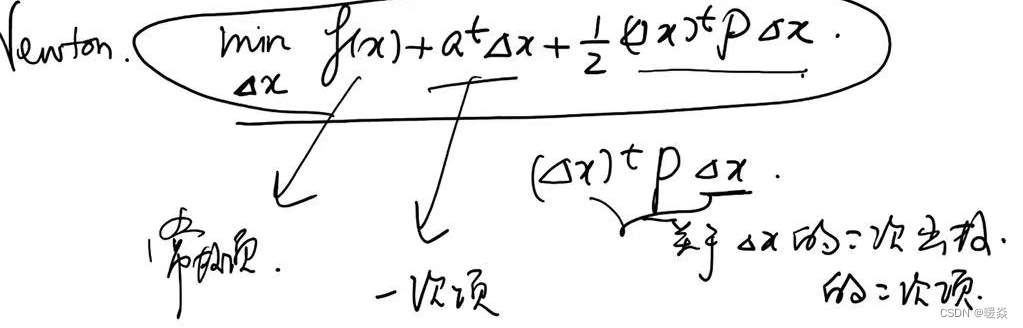
如何找到二阶泰勒展开式的最优解(最小值)?- 梯度=0
令 g ( Δ x ) = m i n Δ x ( f ( x ) + a t Δ x + 1 2 ( Δ x ) t P Δ x ) g(\Delta x)=\underset {\Delta x}{min} (f(x)+a^t \Delta x+\frac 1 2 (\Delta x)^t P \Delta x) g(Δx)=Δxmin(f(x)+atΔx+21(Δx)tPΔx),对 g ( Δ x ) g(\Delta x) g(Δx)求关于 Δ x \Delta x Δx的微分,即梯度 ∇ g \nabla g ∇g,令 ∇ g = 0 \nabla g = 0 ∇g=0,求出 Δ x = − P − 1 a = − ( ∇ 2 f ( x ) ) − 1 ( ∇ f ( x ) ) \Delta x = -P^{-1}a=-(\nabla^2f(x))^{-1}(\nabla f(x)) Δx=−P−1a=−(∇2f(x))−1(∇f(x))即为最优解。实际使用时,为了防止 ( ∇ 2 f ( x ) ) − 1 ( ∇ f ( x ) ) (\nabla^2f(x))^{-1}(\nabla f(x)) (∇2f(x))−1(∇f(x))过大,偏移过远,拟合不准确的问题,需要添加学习率 λ \lambda λ,即 Δ x = − λ ( ∇ 2 f ( x ) ) − 1 ( ∇ f ( x ) ) \Delta x =-\lambda(\nabla^2f(x))^{-1}(\nabla f(x)) Δx=−λ(∇2f(x))−1(∇f(x))。
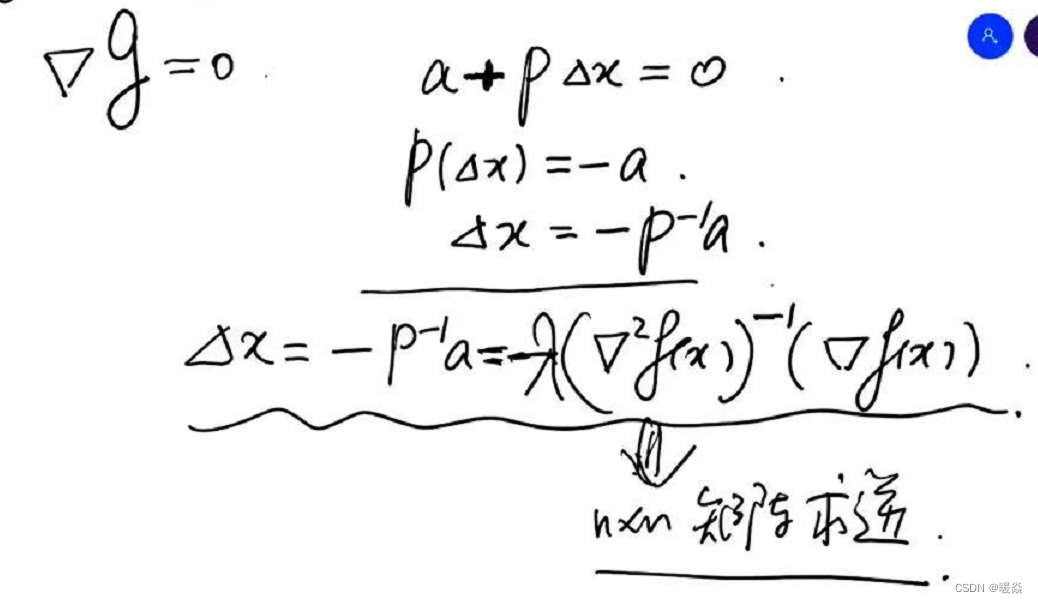
缺点:求解Hessian矩阵的复杂度很高。所以如果Hessian矩阵没有快速计算的方法就会导致迭代过慢,所以牛顿法没有梯度下降法使用频率高。
分类&回归
线性分析
常用不等式
绝对值不等式
∣ a 1 + ⋅ ⋅ ⋅ + a n ∣ ≤ ∣ a 1 ∣ + ⋅ ⋅ ⋅ + ∣ a n ∣ |a_1 + · · · + a_n| \le |a_1| + · · · + |a_n| ∣a1+⋅⋅⋅+an∣≤∣a1∣+⋅⋅⋅+∣an∣

柯西不等式
< a , b > ≤ ∣ ∣ a ∣ ∣ ⋅ ∣ ∣ b ∣ ∣ <a,b>\le||a|| \cdot ||b|| <a,b>≤∣∣a∣∣⋅∣∣b∣∣
( ∑ i = 1 n a i b i ) 2 ≤ ( ∑ i = 1 n a i 2 ) ( ∑ i = 1 n b i 2 ) (\sum_{i=1}^n a_i b_i)^2 \le (\sum_{i=1}^n a_i^2)(\sum_{i=1}^n b_i^2) (∑i=1naibi)2≤(∑i=1nai2)(∑i=1nbi2)
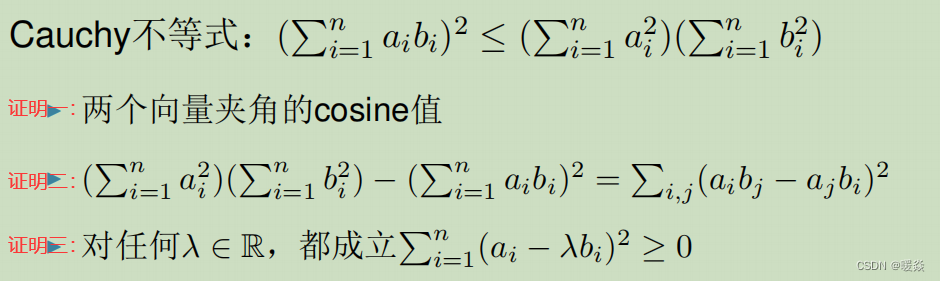

数学研究问题,从群(加)到线性空间(加乘),到赋范线性空间(距离)再到hilbert空间(几何(角度))。
内积的概念很重要,因为有了内积就有了几何结构。
算术-几何平均不等式


数列极限
序列极限
上极限
下极限

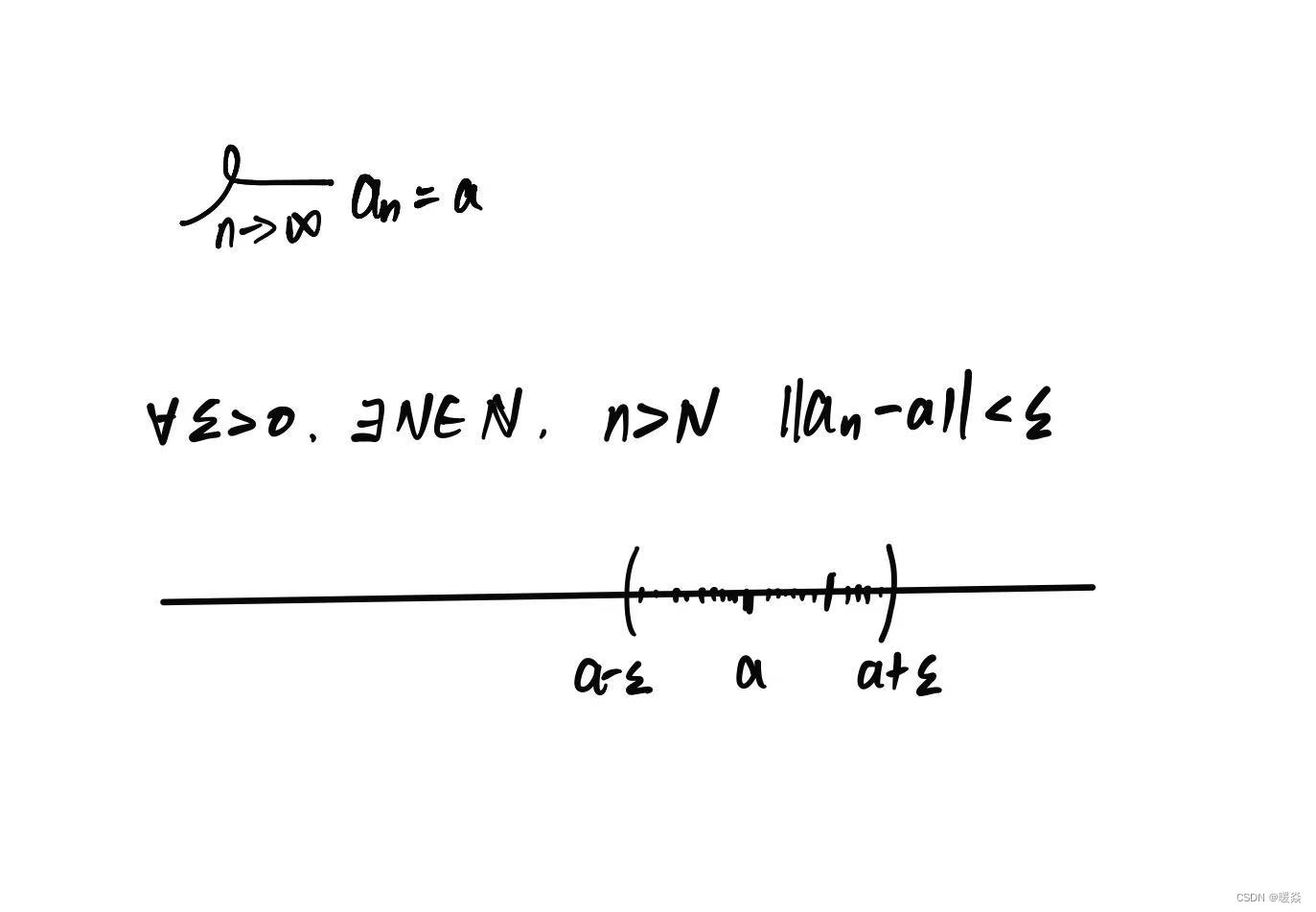
级数
无穷数列和。
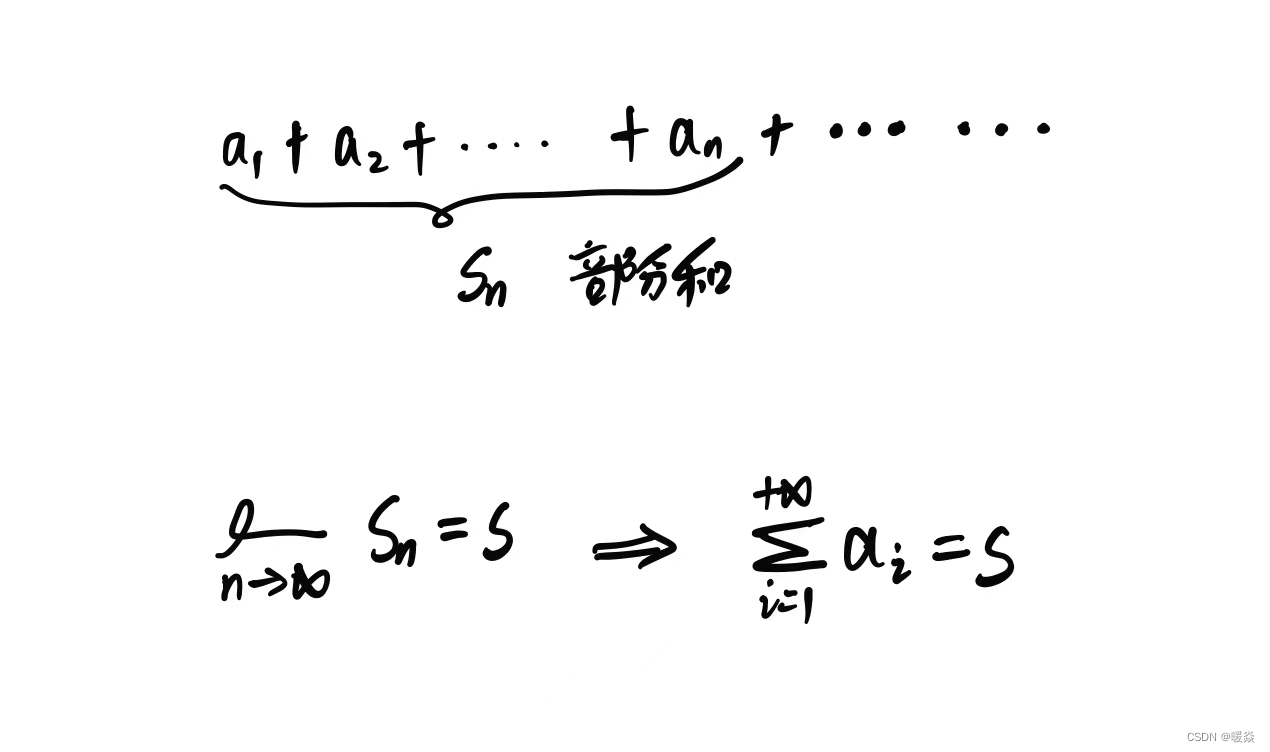

点集拓扑

开集
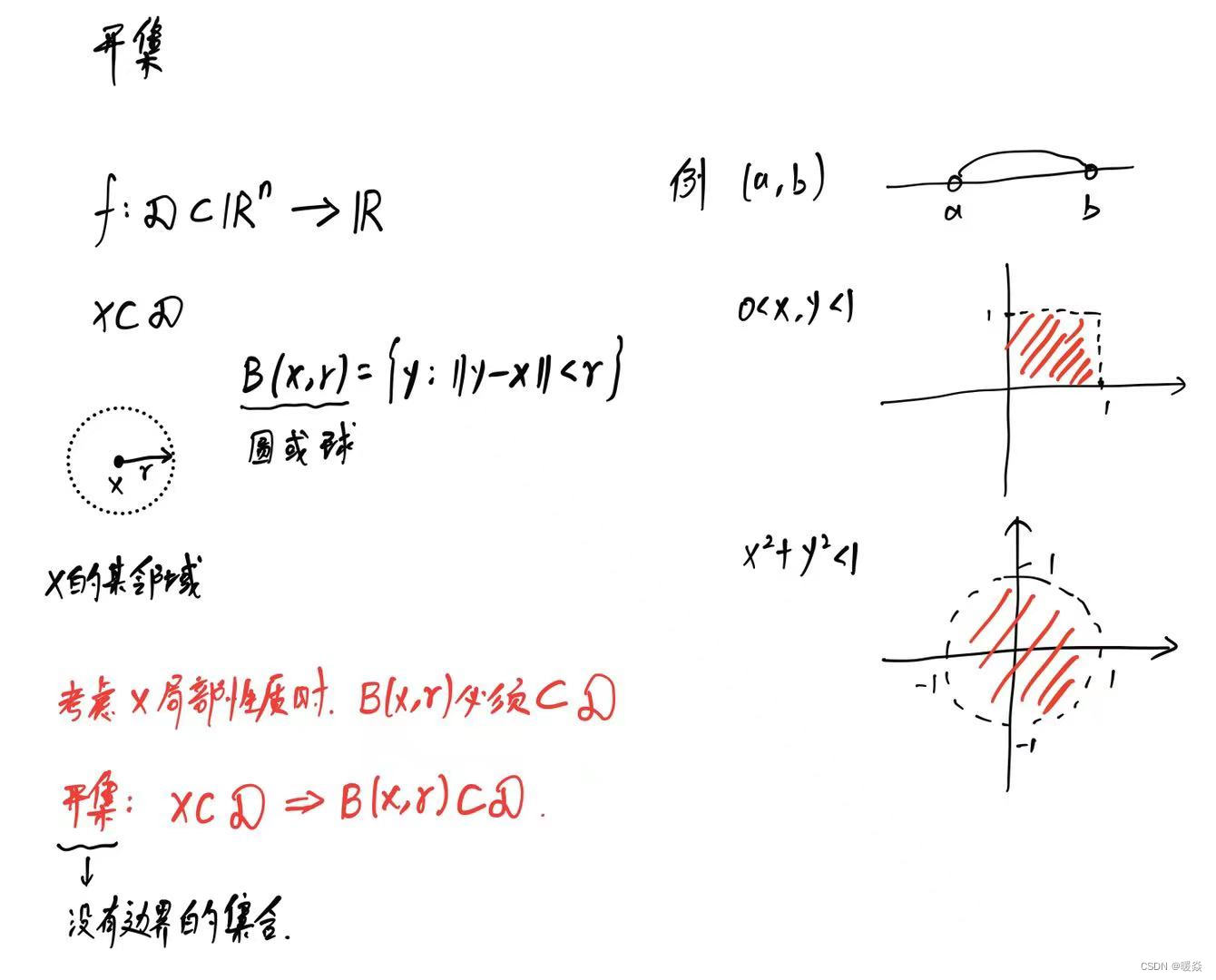
开集性质
任意个开集之并是开集,有限个开集之交是开集。
闭集
“闭”:包含极限点。

闭集性质
任意个闭集之交是闭集,有限个闭集之并是闭集。
紧集
有界闭集。
Heine-Borel定理
R n \mathbb{R^n} Rn 上紧集的任何开覆盖都存在有限子覆盖。
例题:判断 R n \mathbb{R^n} Rn和 ∅ \emptyset ∅是否开闭紧?

R n \mathbb{R^n} Rn 不是紧集,因为没有边界。
函数连续性
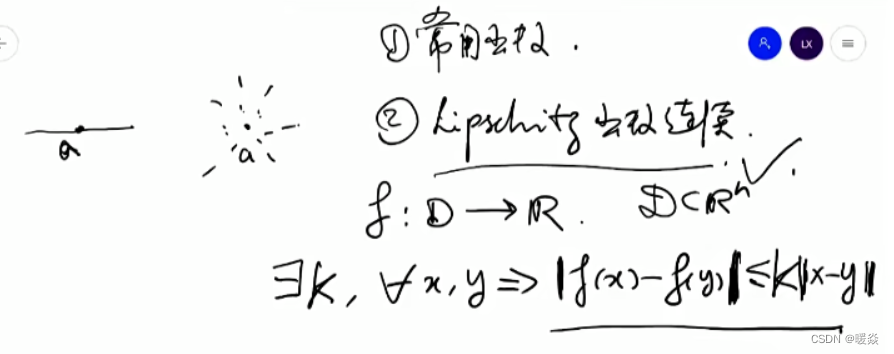
函数连续定义

Lipshitz函数是连续函数

Lipshitz函数与机器学习
参考:Lipschitz函数与机器学习 - gwave的文章 - 知乎
深度学习对输入很敏感,微小的扰动就可能对结果产生很大的影响,将少量精心选择的长臂猿梯度噪声混人熊猫的照片,算法就把熊猫误认为是长臂猿了,Lipschitz常数是种衡量网络稳定性的测度,bound住了输出变化对输入微扰的上限。



连续函数逼近

拉格朗日插值定理


连续函数性质
最值定理

波尔查诺-维尔斯特拉斯定理,又称为致密性定理。指有界数列必有收敛子列。从极限点的角度来叙述致密性定理,就是:有界数列必有极限点。
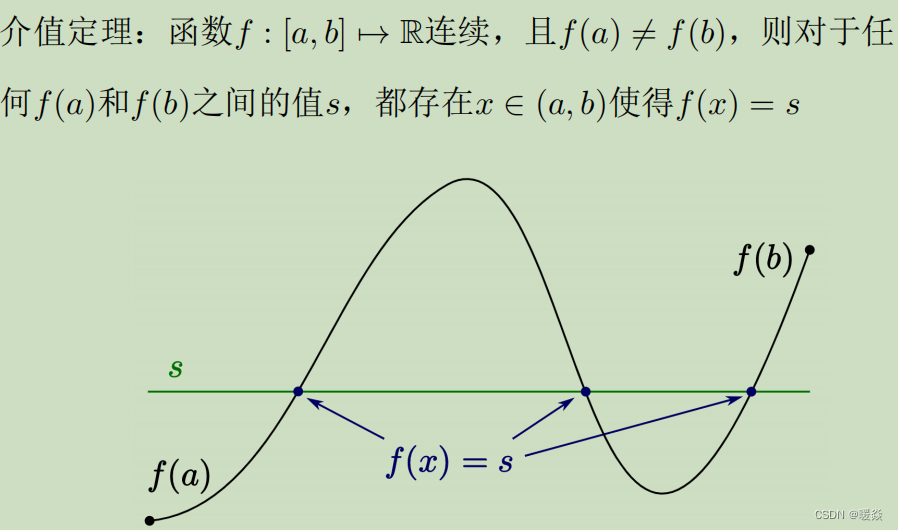
介值定理
不连续函数

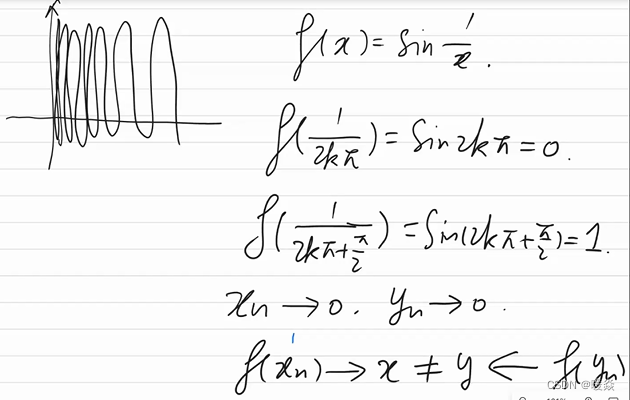
导数
一元函数导数
定义
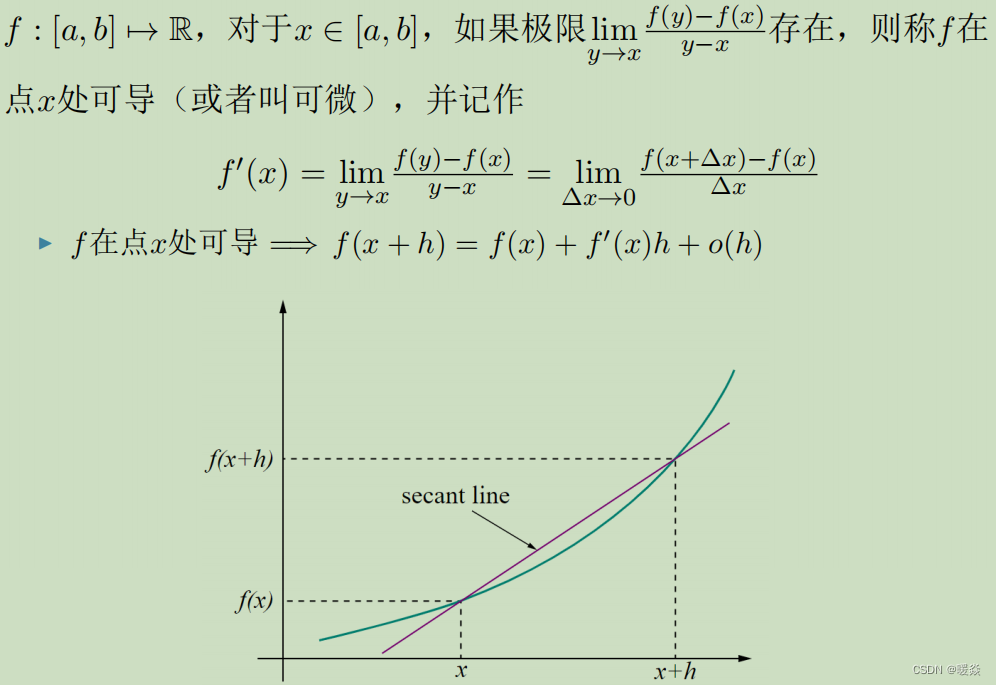
意义

性质
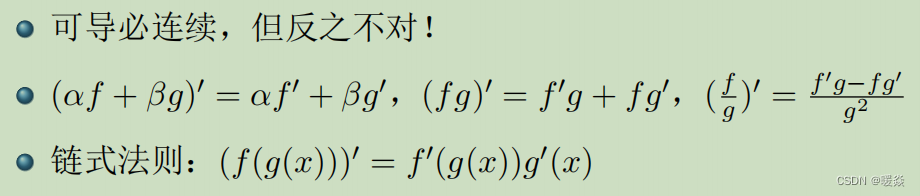
极值定理
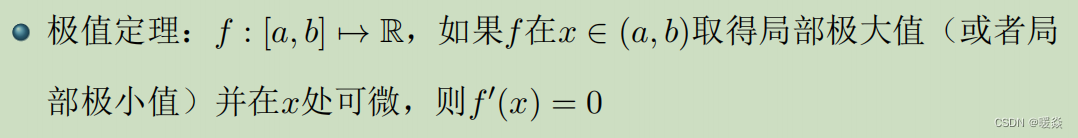
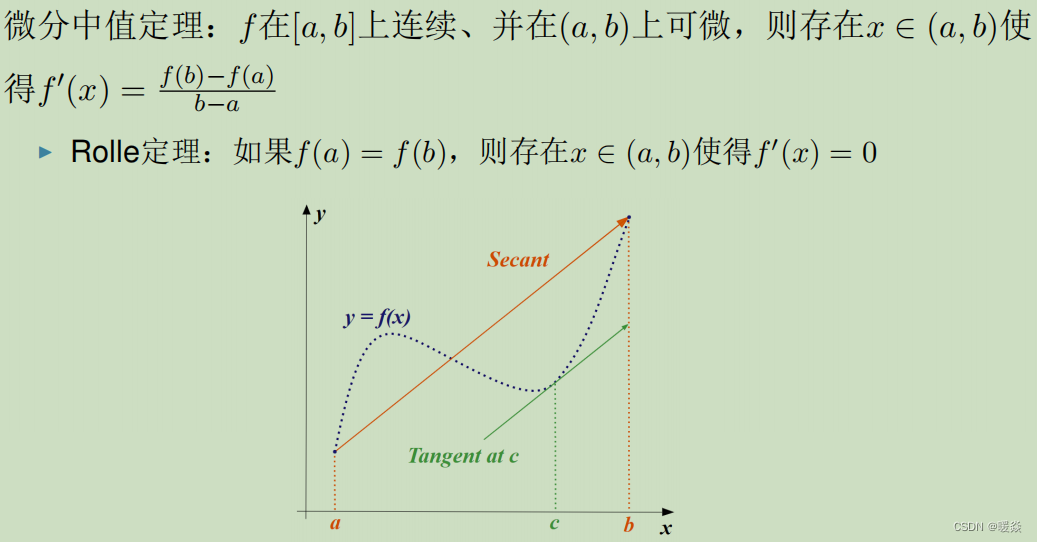
微分中值定理
洛必达法则

常用公式

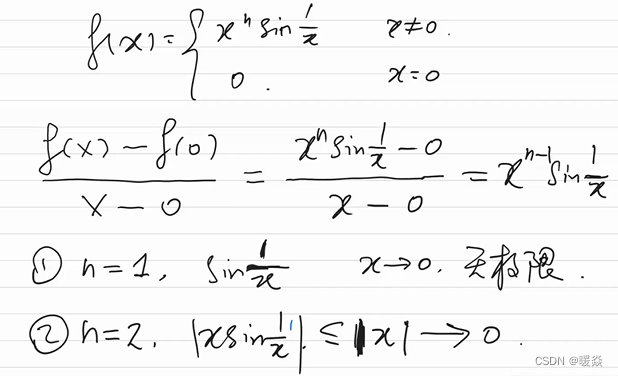
C ∞ C^\infty C∞
C
1
C^1
C1:函数一阶导数存在。
C
2
C^2
C2:函数二阶导数存在。
C
3
C^3
C3:函数三阶导数存在。
…
C
∞
C^\infty
C∞:函数任意阶导数都存在。
多元多值函数
可微
梯度存在
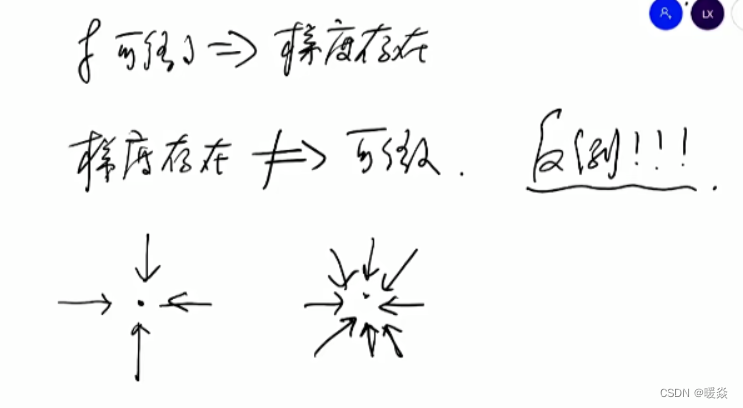
什么情况下梯度存在可以推出函数可微?