一直对np的线性运算不太清晰，正好上课讲到了，做一个笔记整个理解一下 

1.向量和矩阵

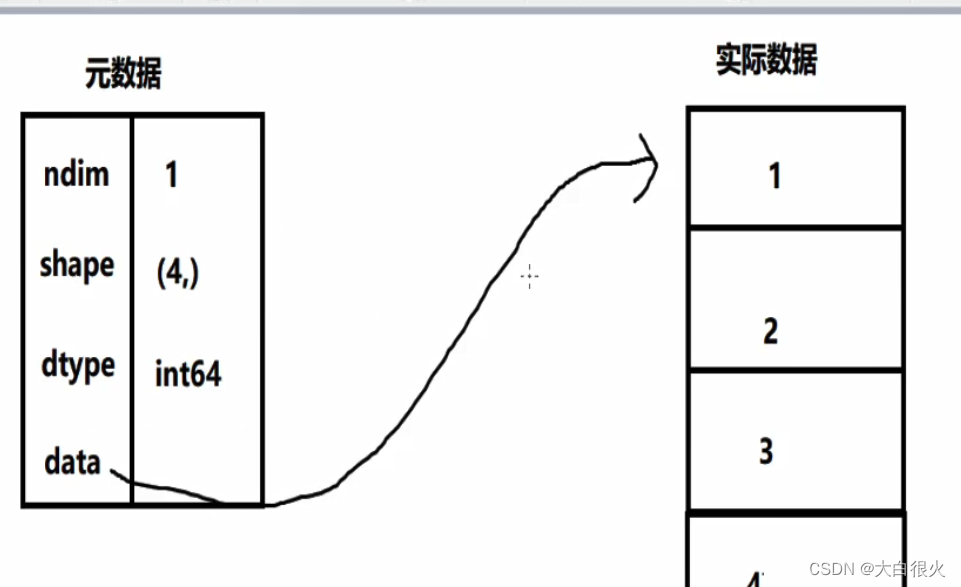
在numpy中，一重方括号表示的是向量vector，vector没有行列的概念。二重方括号表示矩阵matrix，有行列。

 

代码显示如下：

import numpy as np
a=np.array([1,2,3])
a.shape
#(3,)
b=np.array([[1,2,3],[3,4,5]])
b.shape
#(2, 3)
c=np.array([[1],[2],[3]])
c.shape
#(3, 1)

即使[1,2,3]、[[1,2,3]]看起来内容一样 使用过程中也会有完全不一样的变化。下面以向量乘法为例解释。

2.向量和向量乘法

1.* 对应对应位置相乘

普通的*：在numpy里表示普通的对应位置相乘，注意相乘的两个向量、矩阵要保证维数相同

a1=np.array([1,2,3])
a2=np.array([1,2,3])
a1*a2
#array([1, 4, 9])

b1=np.array([[1,2,3]])
b2=np.array([[1,2,3]])
b1*b2
#array([[1, 4, 9]])

b1=np.array([[1,2,3],[3,4,5]])
b2=np.array([[1,2,3],[3,4,5]])
b1*b2
# array([[ 1,  4,  9],
#        [ 9, 16, 25]])

2.广播机制

如果单纯出现维数对不上，python会报error

b1=np.array([[1,2]])
b2=np.array([[1,2,3]])
b1*b2
#operands could not be broadcast together with shapes (1,2) (1,3) 

但是，还有一种情况会出现乘出来一个好大的矩阵，这个情况常出现在无意之中把行、列的数字搞反的情况下。被称为广播机制，需要两个乘子都有一个维数是1，如果是对不上且不为1就会报错

Numpy中的广播机制，你确定正确理解了吗？ - 腾讯云开发者社区-腾讯云

在普通的对应位置相乘，会出现 

a1=np.array([1,2,3])
a3=np.array([[1],[2],[3]])
a1*a3#broadcast together
# array([[1, 2, 3],
#        [2, 4, 6],
#        [3, 6, 9]])

倒过来也会出现

a1=np.array([1,2,3])
a3=np.array([[1],[2],[3]])
a3*a1#broadcast together
# array([[1, 2, 3],
#        [2, 4, 6],
#        [3, 6, 9]])

3.向量点乘np.dot

必须要(行向量，列向量）形式的输入

a1=np.array([1,2,3])
a3=np.array([[1],[2],[3]])
np.dot(a3,a1)
#array([14])
#ValueError: shapes (3,1) and (3,) not aligned: 1 (dim 1) != 3 (dim 0)

 都是行向量，不行

b1=np.array([[1,2,3]])
b2=np.array([[1,2,3]])
np.dot(b1,b2) 
#shapes (1,3) and (1,3) not aligned: 3 (dim 1) != 1 (dim 0)

都是列向量，触发广播机制

a1=np.array([[1,2,3]])
a3=np.array([[1],[2],[3]])
np.dot(a3,a1)
# array([[1, 2, 3],
#        [2, 4, 6],
#        [3, 6, 9]])

3.矩阵和向量乘法

1.对应位置相乘

如果单纯采用*的方式进行矩阵和向量乘法，那就是广播机制

矩阵+向量

A1=np.array([[1,2,3],[2,3,4]])
b1=np.array([1,2,3])
A1*b1 #broadcast together
# array([[ 1,  4,  9],
#        [ 2,  6, 12]])

 对应的向量如果是矩阵形式，结果相同

A2=np.array([[1,2,3],[2,3,4]])
b2=np.array([[1,2,3]])
A2*b2 #broadcast together
# array([[ 1,  4,  9],
#        [ 2,  6, 12]])

相似的，如果维数对不上，不会触发广播机制

A3=np.array([[1,2,3],[2,3,4]])
b3=np.array([[1],[2],[3]])
A3*b3 #operands could not be broadcast together with shapes (2,3) (3,1) 

2.矩阵乘法

如果真正想要算矩阵*向量的矩阵乘法，要用np.dot

A4=np.array([[1,2,3],[2,3,4]])
b4=np.array([1,2,3])
np.dot(A4,b4)#dot product
#array([14, 20])

列向量也有类似结果

A4=np.array([[1,2,3],[2,3,4]])
b4=np.array([[1],[2],[3]])
np.dot(A4,b4)#dot product
# array([[14],
#        [20]])

4.矩阵矩阵乘法：

1.直接相乘

同样，也是对应位置相乘

A4=np.array([[1,2,3],[2,3,4]])
B4=np.array([[1,2,3],[4,5,6]])
A4*B4
# array([[ 1,  4,  9],
#        [ 8, 15, 24]])

 有广播机制

A4=np.array([[1,2,3],[2,3,4]])
B4=np.array([[1,2,3]])
A4*B4
# array([[ 1,  4,  9],
#        [ 2,  6, 12]])

2.np.dot:

需要第一个的列数和第二个的行数相对应

A4=np.array([[1,2,3],[2,3,4]])
B4=np.array([[1,2,3],[4,5,6]])
np.dot(A4,B4.T)
# array([[14, 32],
#        [20, 47]])

A5=np.array([[1,2,3],[2,3,4]])
B5=np.array([[1,2,3],[4,5,6],[7,8,9]])
np.dot(A5,B5)
# array([[30, 36, 42],
#        [42, 51, 60]])

对不上会报错

A4=np.array([[1,2,3],[2,3,4]])
B4=np.array([[1,2,3],[4,5,6]])
np.dot(A4,B4)
# shapes (2,3) and (2,3) not aligned: 3 (dim 1) != 2 (dim 0)