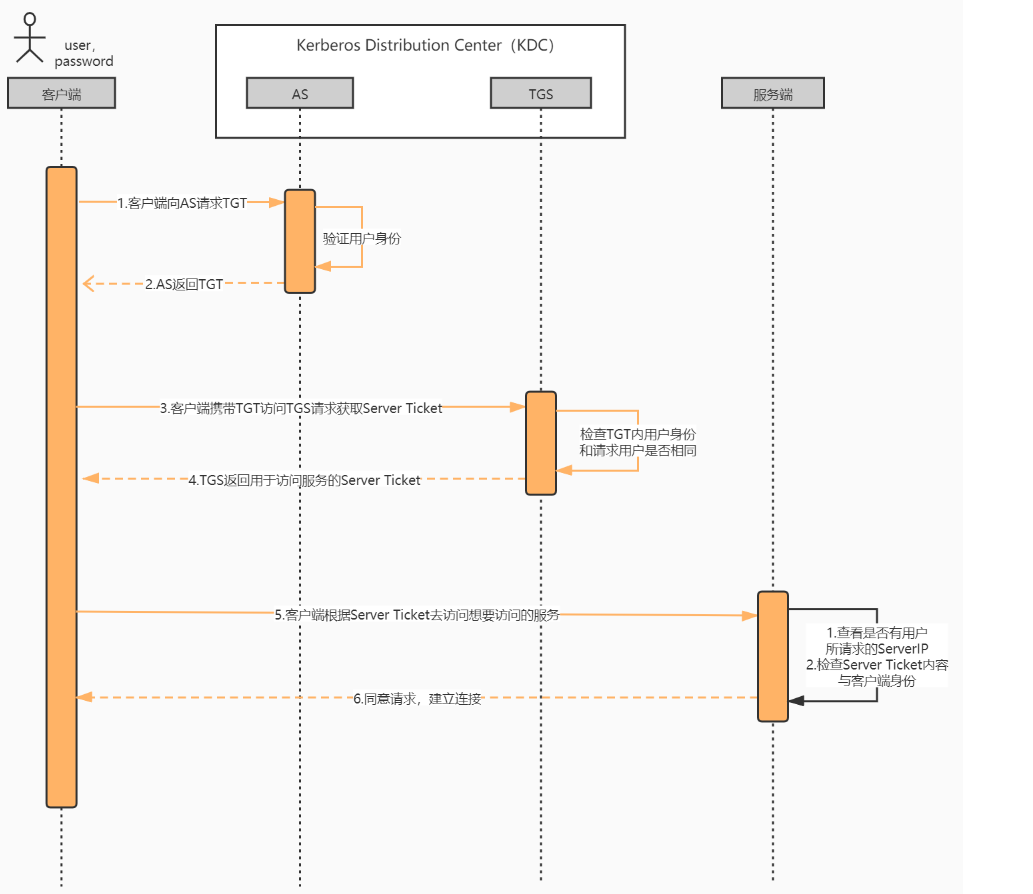
之前我们就讲过队列，栈的基础知识，笔者之前有过详细的介绍，感兴趣的可以根据笔者的个人主页进行查找：https://blog.csdn.net/weixin_64308540/?type=lately

225. 用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

• void push(int x) 将元素 x 压入栈顶。

• int pop() 移除并返回栈顶元素。

• int top() 返回栈顶元素。

• boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

• 你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。

• 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：

["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]

输出：

[null, null, null, 2, 2, false]

解释：

MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

提示：

• 1 <= x <= 9

• 最多调用100 次 push、pop、top 和 empty

• 每次调用 pop 和 top 都保证栈不为空

进阶：你能否仅用一个队列来实现栈。

首先我们需要知道的是：

队列：先进先出  栈：先进后出模式，所以，一个队列不能实现栈，只能用两个队列！！

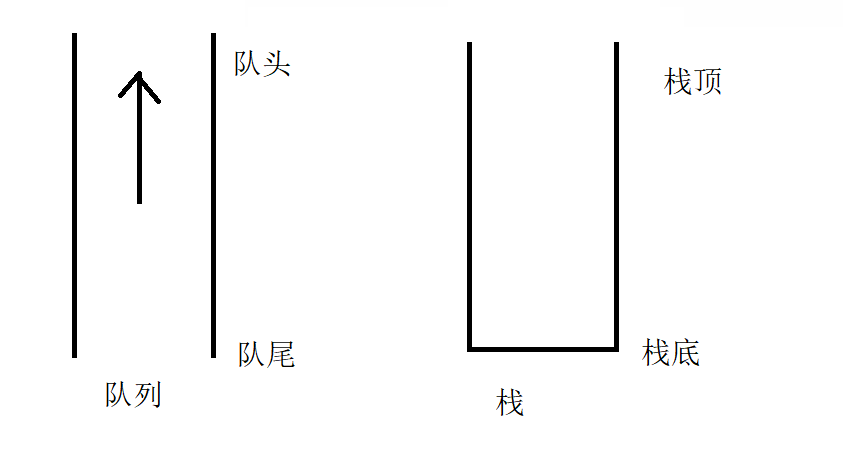
我们在MyStack文件：

首先，我们需要定义一个两个队列：

 private Queue<Integer> qu1;
 private Queue<Integer> qu2;    

然后，我们需要对这两个队列进行初始化：

   //初始化两个队列
    public MyStack(){
        qu1=new LinkedList<>();
        qu2=new LinkedList<>();
    }
    

接下来，我们就需要进入真正的主题了：

1. 将元素压入栈

    // 将元素压入栈  找不为空的队列
    public void push(int x){
        if (!qu1.isEmpty()){
            qu1.offer(x);
        }else if (!qu2.isEmpty()){
            qu2.offer(x);
        }else {
            qu1.offer(x);
        }
    }

将元素压入栈，这个思路很简单！！（主要还是要找不为空的队列）

qu1与qu2两个队列，哪个队列不为空，就放哪个，如果两个队列都为空，则放qu1队列！！

2. 移除并且返回栈顶元素

    //移除并且返回栈顶元素
    //出栈并返回，出size-1个元素，到另一个队列中
    public int pop(){
        if (empty()){
            return -1;//如果两个队列都为空，则说明，当前栈为空
        }
        if (!qu1.isEmpty()){
            int size=qu1.size();
            for (int i = 0; i < size-1; i++) {
                int val=qu1.poll();
                qu2.offer(val);
            }
            return qu1.poll();
            //最后qu1剩余1个，就是我们想要移除的
        }else {
            int size=qu2.size();
            for (int i = 0; i < size-1; i++) {
                int val=qu2.poll();
                qu1.offer(val);
            }
            return qu2.poll();
            //最后qu2剩余1个，就是我们想要移除的
        }
    }

在这个思路中，我们需要将第一个栈（不为空）的size个元素，移到第二个栈（为空）的里面，最后所剩余的哪一个，就是我们想要移除的元素！

在这里，我们用到了：判断栈是否为空：

  //如果栈是空的，则返回true,否则，返回false
    public boolean empty(){
        return qu1.isEmpty() && qu2.isEmpty();
        //确保两个队列都不为空
    }

3. 返回栈顶元素（peek()偷看）

    //返回栈顶元素（peek()偷看）
    public int pop(){
        if (empty()){
            return -1;
        }
        if (!qu1.isEmpty()){
            int size=qu1.size();
            int val=-1;
            for (int i = 0; i < size; i++) {
                val=qu1.poll();
                qu2.offer(val);
            }
            return val;
        }else {
            int size=qu2.size();
            int val=-1;
            for (int i = 0; i < size; i++) {
                val=qu2.poll();
                qu1.offer(val);
            }
            return val;
        }
    }

主要的思路：判断是否为空：若qu1不为空，则通过val将qu1中的数据全部转移到qu2中，最后一次转移的值，就是我们想要的！

232. 用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

• void push(int x) 将元素 x 推到队列的末尾

• int pop() 从队列的开头移除并返回元素

• int peek() 返回队列开头的元素

• boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

• 你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。

• 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：

["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]

输出：

[null, null, null, 1, 1, false]

解释：

MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

提示：

• 1 <= x <= 9

• 最多调用 100 次 push、pop、peek 和 empty

• 假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）

进阶：

• 你能否实现每个操作均摊时间复杂度为 O(1) 的队列？换句话说，执行 n 个操作的总时间复杂度为 O(n) ，即使其中一个操作可能花费较长时间。

初始准备阶段:准备两个栈：

   private Stack<Integer> stack1;
    private Stack<Integer> stack2;

然后我们在对准备好的两个栈，进行初始化：

  public MyQueue() {
        stack1=new Stack<>();
        stack2=new Stack<>();
    }

下面，我们就开始步入正轨：

1. 将元素x 推到队列的队尾：

  //将元素x推到队列的末尾
    public void push(int x){
        stack1.push(x);
        //往栈中放入元素，全部放入第一个栈中
    }

2. 从队列的开头移除并返回元素：

  //从队列的开头移除并返回元素：
    public int pop(){
        if (empty()){
            return -1;
        }
        if (stack2.empty()){
            while (!stack1.empty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();//将第2个栈的栈顶元素出栈
    }

在这个过程中：我们规定，第一个栈：输入栈，第二个栈：输出栈，当第二个栈为空时，则将第一个栈的所有元素都导入第二个栈中

3. 在这个代码中，我们自己定义了一个：判断栈是否为空的函数：

 //如果队列为空，返回true,否则返回false
    public boolean empty(){
        return stack1.empty() && stack2.empty();
    }

4. 返回队列开头的元素（偷看）

   //返回队列开头的元素（偷看）
    public int peek(){
        if (empty()){
            return -1;
        }
        if (stack2.empty()){
            while (!stack1.empty()){
                stack2.push(stack1.pop());
            }
        }
        //偷看，第2个栈的栈顶元素
        return stack2.peek();
    }

在上述的两个列题中，我们分别用用队列实现栈，用栈实现队列，作为两个小小的列题，我们最后可以得出一下规律：

- 用队列实现栈：

- 优点：因为栈是后进先出的结构，用队列可以有效的实现这一性质，即添加元素为一个队列的末端，而移除元素只允许从另一个队列的末端移除。

- 缺点：实现较为复杂，需要两个队列来进行实现，还需要额外的空间来存储数据。

- 用栈实现队列：

- 优点：实现简单，只需要用一个栈来存储数据，另一个栈仅仅用于存储另一个栈的临时元素。

- 缺点：由于栈只能实现先进后出的结构，它不能有效的实现队列的先进先出的特性。