加入bing体验chatGPT大军中来吧，它来了！

news2024/11/14 19:12:45

1 第一步：加入候选名单

1、首先需要加入候选名单

  • https://www.microsoft.com/zh-cn/edge?form=MA13FJ
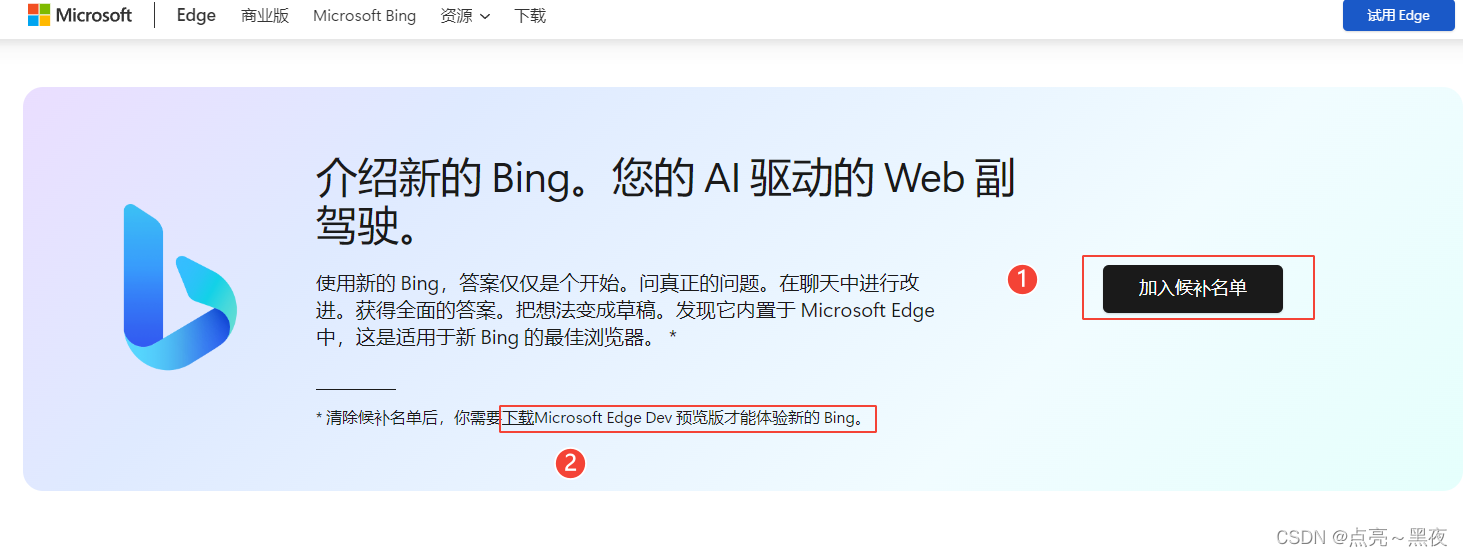
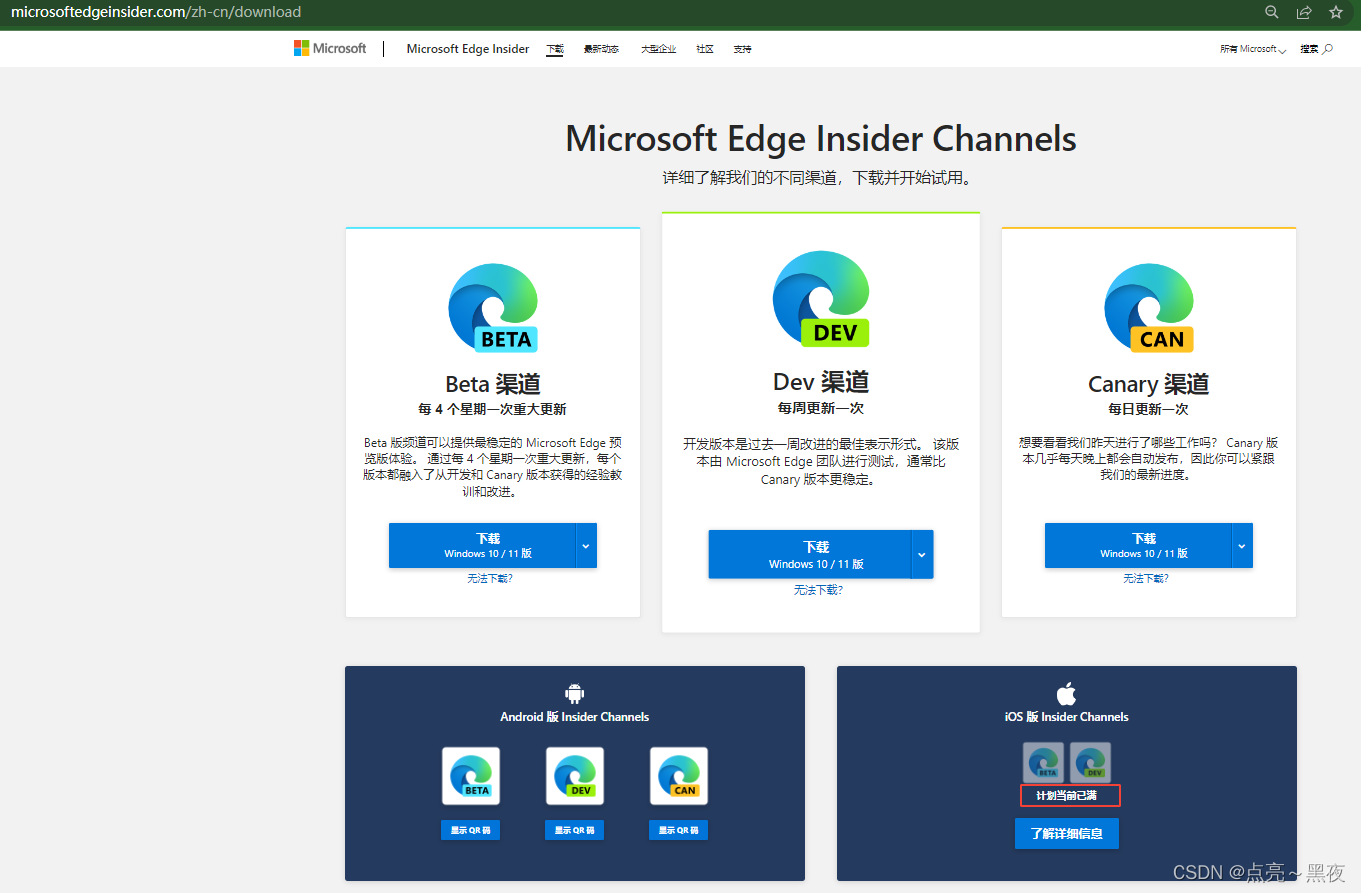
    在这里插入图片描述

2、下载最新的Edge浏览器、androd、iOS都有试用版本（可以看到iOS加护当前已满）

这里我下载的是dev版本，Canary版本由于是每日更新，可能会有bug，而且当前Canary还不支持设置为默认浏览器！
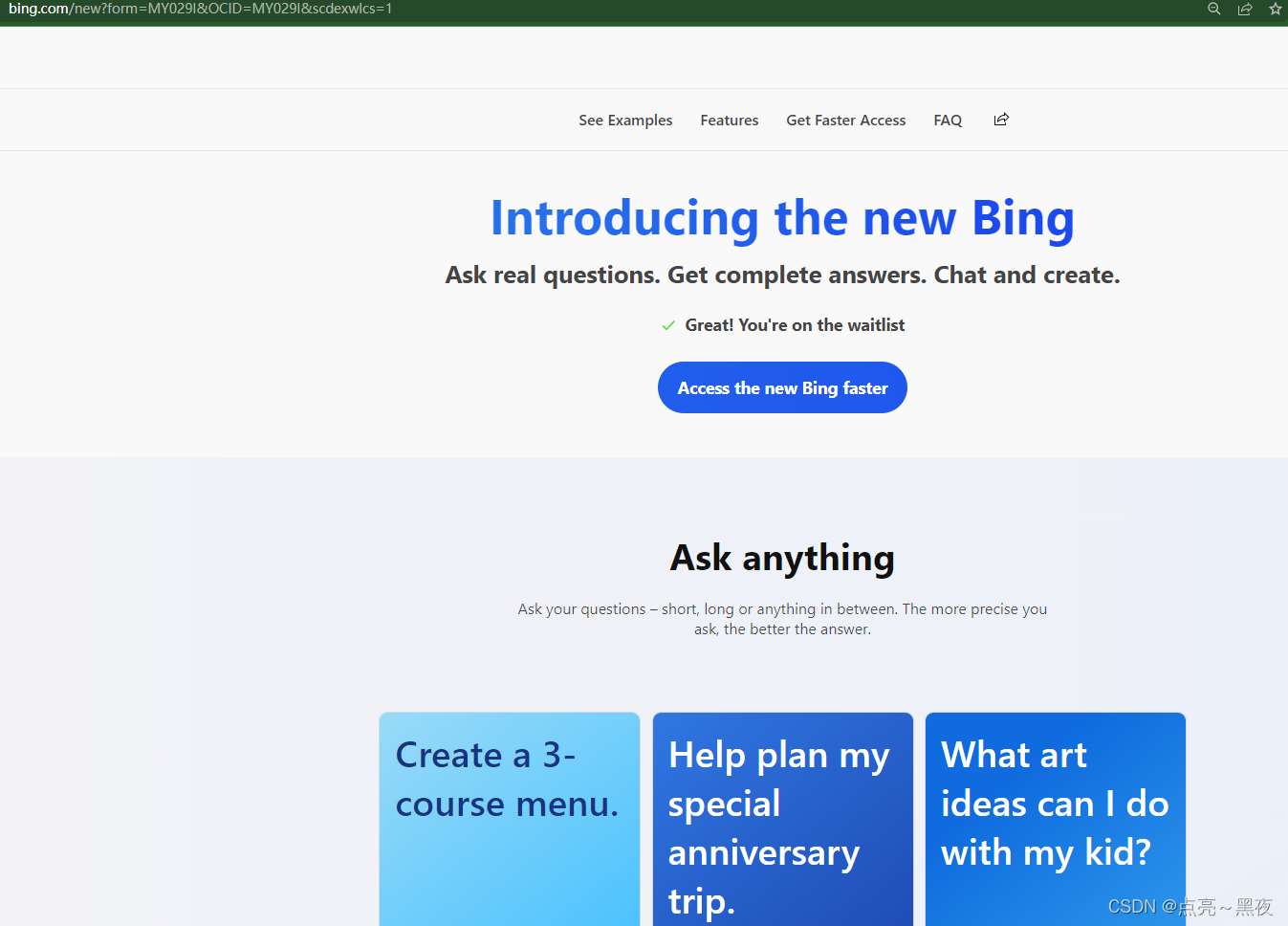
在这里插入图片描述

3、我已经加入排队的大军（https://www.bing.com/new?form=MY029I&OCID=MY029I&scdexwlcs=1）

在这里插入图片描述

4、下载Edge dev浏览器，安装好之后，把Edge设置为默认浏览器
在这里插入图片描述

4、打开安装的浏览器，可以看到我已经进入后补名单，后面就等待体验吧！
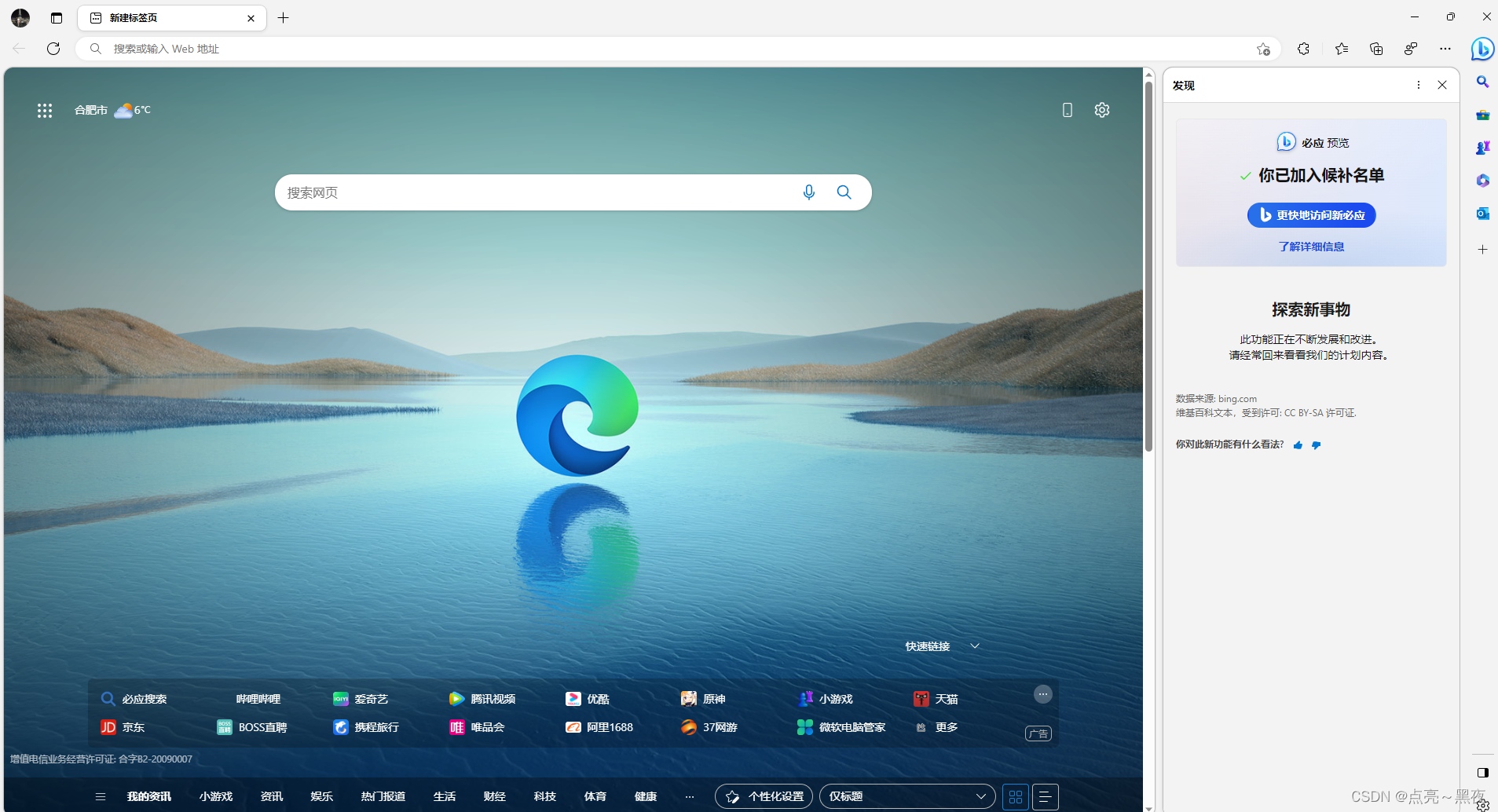
在这里插入图片描述

2 第二步：开始体验

waiting…

The countdown from 20230209 15:52

它来了，2023.02.13 ！！！

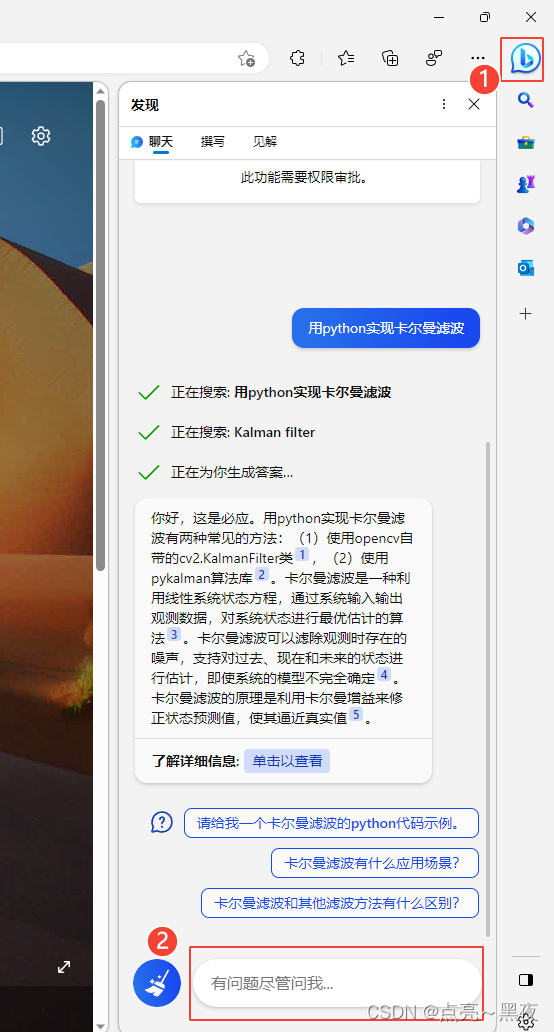
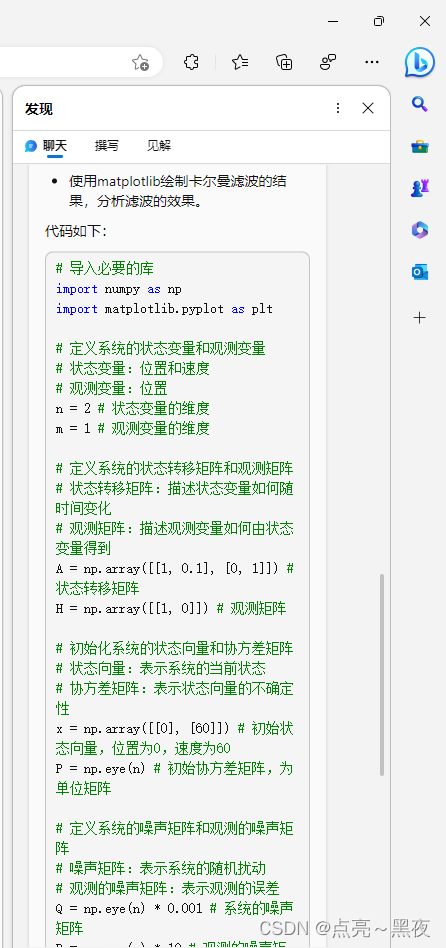
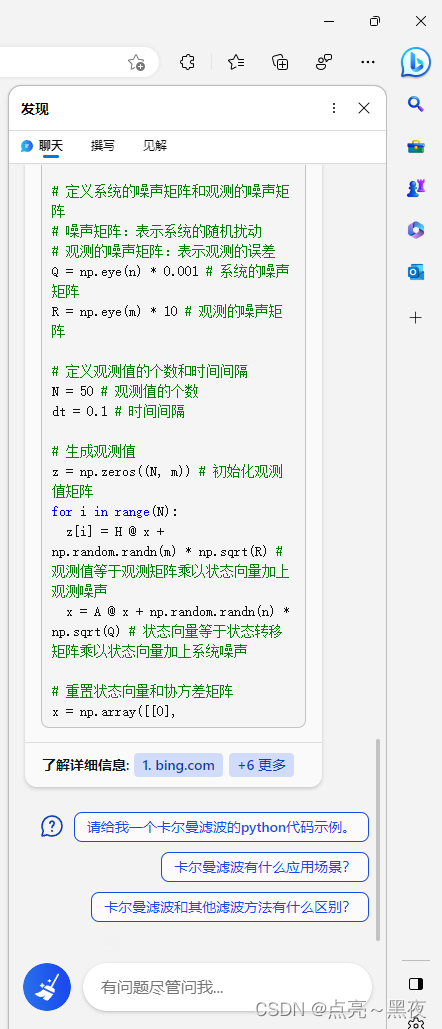
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/341420.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

50. Pow(x, n)

50. Pow(x, n)

50. Pow(x, n) 一、题目描述： 实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。 示例 1： 输入：x 2.00000, n 10 输出：1024.00000 示例 2： 输入：x 2…
阅读更多...
决策树分类算法（一）（信息熵，信息增益，基尼指数计算）

决策树分类算法（一）（信息熵，信息增益，基尼指数计算）

目录一、信息量二、信息熵三、信息增益四、基尼指数五、代码：信息熵，信息增益，基尼指数计算（splitInfo.py）例子： 一、信息量 : I(x)log⁡21p−log⁡2pI(x)\log_{2}{\frac{1}{p}}-\log_{2}{p}I(x)log2​p1…
阅读更多...
傻白探索Chiplet，Modular Routing Design for Chiplet-based Systems（十一）

傻白探索Chiplet，Modular Routing Design for Chiplet-based Systems（十一）

阅读了Modular Routing Design for Chiplet-based Systems这篇论文，是关于多chiplet通信的，个人感觉核心贡献在于实现了 deadlock-freedom in multi-chiplet system，而不仅仅是考虑单个intra-chiplet的局部NoC可以通信，具体的一些…
阅读更多...
如何判断两架飞机在汇聚飞行？（如何计算两架飞机的航向夹角？）内含程序源码

如何判断两架飞机在汇聚飞行？（如何计算两架飞机的航向夹角？）内含程序源码

ok，在开始一切之前，让我先猜一猜，你是不是想百度“二维平面下如何计算两个移动物体的航向夹角？”如果是，那就请继续往下看。 首先，我们要明确一个概念：航向角≠航向夹角！&#xff0…
阅读更多...
微信小程序图书馆座位预约管理系统

微信小程序图书馆座位预约管理系统

开发工具：IDEA、微信小程序服务器：Tomcat9.0， jdk1.8项目构建：maven数据库：mysql5.7前端技术：vue、uniapp服务端技术：springbootmybatis本系统分微信小程序和管理后台两部分，项目采用…
阅读更多...
家政服务小程序实战教程05-集成腾讯地图

家政服务小程序实战教程05-集成腾讯地图

我们在用户注册数据源部分设计了一个地图字段，地图字段在生成页面的时候对应着地图定位组件 要调用地图定位组件，需要先创建API，点击新建API 选择腾讯地图 创建API的时候需要输入API key 进入到腾讯位置服务里申请Key 首先需要创建一个应用 创…
阅读更多...
Go 全栈博客实战项目 gin-vue-blog

Go 全栈博客实战项目 gin-vue-blog

Go 全栈博客 gin-vue-blog写在前面博客介绍在线预览项目介绍技术介绍目录结构环境介绍线上环境开发环境VsCode 插件快速开始拉取项目前的准备 (Windows)方式一：Docker Compose 一键运行方式二：常规运行项目部署总结鸣谢后续计划写在前面 这个项目其实已经…
阅读更多...
Dubbo和Zookeeper集成

Dubbo和Zookeeper集成

分布式理论 什么是分布式系统？ 在《分布式系统原理与范型》一书中有如下定义：“分布式系统是若干独立计算机的集合，这些计算机对于用户来说就像单个相关系统”； 分布式系统是由一组通过网络进行通信、为了完成共同的任务而协调…
阅读更多...
分享111个助理类简历模板，总有一款适合您

分享111个助理类简历模板，总有一款适合您

分享111个助理类简历模板，总有一款适合您 111个助理类简历模板下载链接：https://pan.baidu.com/s/1JafYuLPQMmq37K4V0wiqWA?pwd8y54 提取码：8y54 Python采集代码下载链接：https://wwgn.lanzoul.com/iKGwb0kye3wj 设计师助理…
阅读更多...
浅析SCSI协议（1）基本介绍

浅析SCSI协议（1）基本介绍

概述 SCSI即小型计算机接口（Small Computer System Interface），指的是一个庞大协议体系，到目前为止经历了SCSI-1/SCSI-2/SCSI-3变迁。SCSI协议定义了一套不同设备（磁盘、磁带、处理器、光设备、网络设备等&#xff09…
阅读更多...
C/C++工业数据分析与文件信息管理系统[2023-02-12]

C/C++工业数据分析与文件信息管理系统[2023-02-12]

C/C工业数据分析与文件信息管理系统[2023-02-12] 程序设计基础A课程设计 工业数据分析与文件信息管理系统 题目背景 智能制造是以工业生产数据分析、自动化技术为基础，具有信息深度自感知、智慧优化自决策、精准控制自执行等功能，使制造活动达到安全…
阅读更多...
[golang gin框架] 2.Gin HTML模板渲染以及模板语法,自定义模板函数,静态文件服务

[golang gin框架] 2.Gin HTML模板渲染以及模板语法,自定义模板函数,静态文件服务

一.Gin HTML 模板渲染全部模板放在一个目录里面的配置方法首先在项目根目录新建 templates 文件夹&#xff0c;然后在文件夹中新建 对应的index.html<!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta http…
阅读更多...
图像处理-边缘检测-文献阅读笔记

图像处理-边缘检测-文献阅读笔记

[1]李华琛. 基于opencv图像边缘检测技术[J]. 数字技术与应用, 2016(11):2. 高斯滤波有效抑制噪声&#xff1b;原理&#xff1a;识别图像中亮度改变较为明显的点&#xff0c;本质是采用不同的算子进行边缘检测并进行修整。算子&#xff1a;Laplacian 算子、Scharr 算子、Canny 算…
阅读更多...
Kerberos简单介绍及使用

Kerberos简单介绍及使用

Kerberos作用 简单来说安全相关一般涉及以下方面&#xff1a;用户认证&#xff08;Kerberos的作用&#xff09;、用户授权、用户管理.。而Kerberos功能是用户认证&#xff0c;通俗来说解决了证明A是A 的问题。 认证过程&#xff08;时序图&#xff09; 核心角色/概念 KDC&…
阅读更多...
电子学会2022年12月青少年软件编程（图形化）等级考试试卷（四级）答案解析

电子学会2022年12月青少年软件编程（图形化）等级考试试卷（四级）答案解析

目录 一、单选题(共15题&#xff0c;共30分) 二、判断题(共10题&#xff0c;共20分) 三、编程题(共3题&#xff0c;共50分) 青少年软件编程&#xff08;图形化&#xff09;等级考试试卷&#xff08;四级&#xff09; 一、单选题(共15题&#xff0c;共30分) 1. 运行下列程序…
阅读更多...
day39【代码随想录】动态规划之不同路径、不同路径||、最小路径和

day39【代码随想录】动态规划之不同路径、不同路径||、最小路径和

文章目录前言一、不同路径&#xff08;力扣62&#xff09;二、不同路径||&#xff08;力扣63&#xff09;三、最小路径和&#xff08;力扣64&#xff09;前言 1、不同路径 2、不同路径|| 3、最小路径和 一、不同路径&#xff08;力扣62&#xff09; 一个机器人位于一个 m x n…
阅读更多...
Spark09: Spark之checkpoint

Spark09: Spark之checkpoint

一、checkpoint概述 checkpoint&#xff0c;是Spark提供的一个比较高级的功能。有时候&#xff0c;我们的Spark任务&#xff0c;比较复杂&#xff0c;从初始化RDD开始&#xff0c;到最后整个任务完成&#xff0c;有比较多的步骤&#xff0c;比如超过10个transformation算子。而…
阅读更多...
使用Python，Opencv检测图像，视频中的猫

使用Python，Opencv检测图像，视频中的猫

使用Python&#xff0c;Opencv检测图像&#xff0c;视频中的猫&#x1f431; 这篇博客将介绍如何使用Python&#xff0c;OpenCV库附带的默认Haar级联检测器来检测图像中的猫。同样的技术也可以应用于视频流。这些哈尔级联由约瑟夫豪斯&#xff08;Joseph Howse&#xff09;训练…
阅读更多...
Ubuntu最新版本(Ubuntu22.04LTS)安装Tftp服务及其使用教程

Ubuntu最新版本(Ubuntu22.04LTS)安装Tftp服务及其使用教程

目录 一、概述 二、在Ubuntu安装Tftp服务器  &#x1f356;2.1 安装tftp服务端&#xff08;tftpd-hpa&#xff09;  &#x1f356;2.2 配置&#xff0c;修改/etc/default/tftpd-hpa  &#x1f356;2.3 创建tftp服务的下载目录  &#x1f356;2.4 重启tftp服务器 三、在Ubun…
阅读更多...
C++高级篇学习笔记

C++高级篇学习笔记

文章目录 前言 本文记录C一些面试难点问题剖析。 1. 左右值和右值引用的作用 左值&#xff1a;可以在左边&#xff0c;表达式结束后依然存在的持久对象&#xff0c;一般有名字&#xff0c;可以取地址。 提示&#xff1a; 前置自加/自减 可以做左值&#xff1b; 右值在右边&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023