目录
- 一、信息量
- 二、信息熵
- 三、信息增益
- 四、基尼指数
- 五、代码:信息熵,信息增益,基尼指数计算(splitInfo.py)
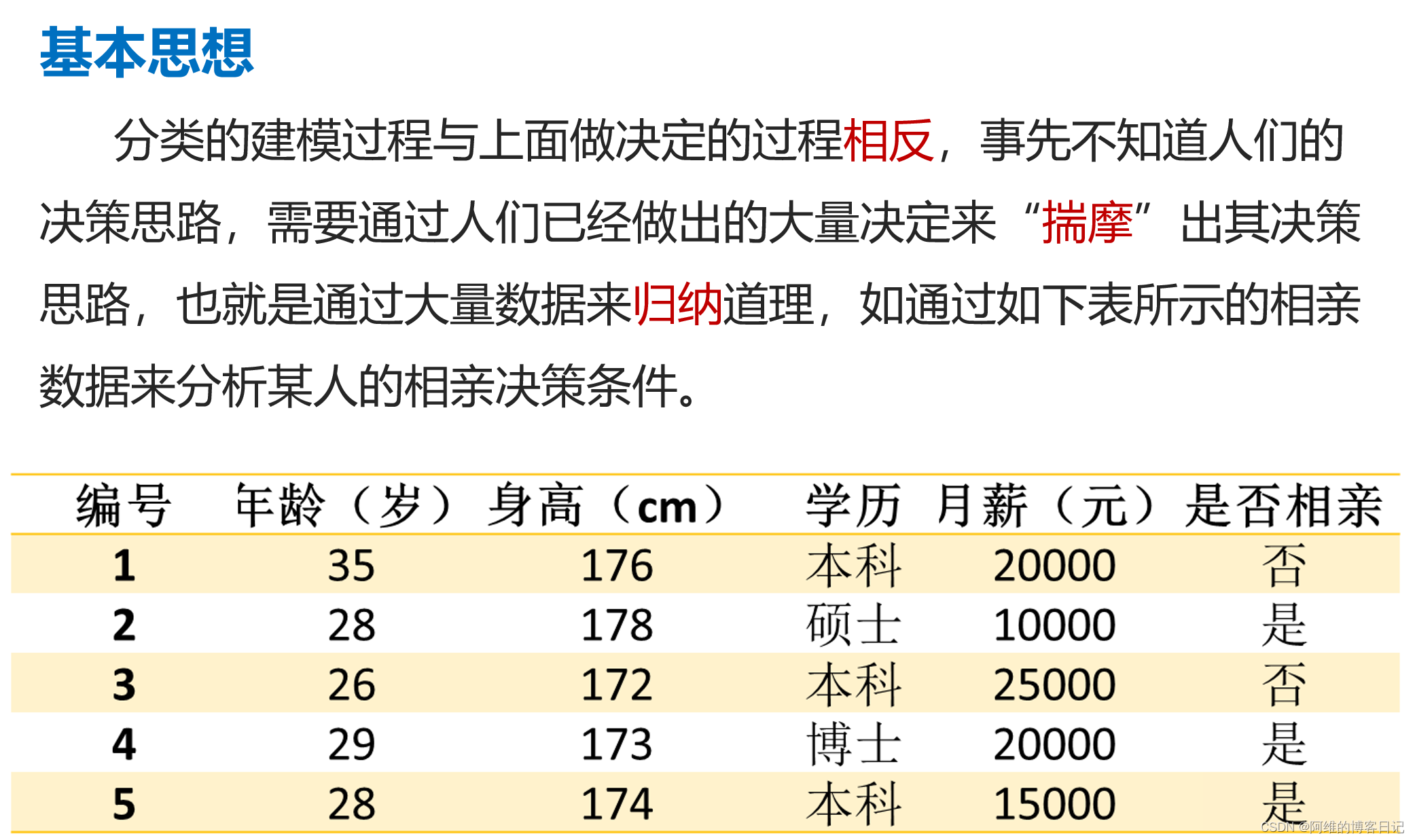
例子:
一、信息量

:
假设中国足球队和巴西足球队曾经有过8次比赛,其中中国队胜1次。以U表示未来的中巴比赛中国队胜的事件,那么U的先验概率就是1/8,因此其信息量就是
如果以 U ‾ \overline{U} U 表示巴西队胜,那么 U ‾ \overline{U} U的先验概率是 7 8 \frac{7}{8} 87,其信息量就是
:
二、信息熵

:

三、信息增益

解释:先把样本分为本科(
3
5
\frac{3}{5}
53)和硕博(
2
5
\frac{2}{5}
52),然后3个本科里面2个不相亲,1个相亲(
2
3
×
log
2
2
3
+
1
3
×
log
2
1
3
\frac{2}{3}\times\log_{2}{\frac{2}{3}}+\frac{1}{3}\times\log_{2}{\frac{1}{3}}
32×log232+31×log231),2个硕博里面都相亲
log
2
1
\log_{2}{1}
log21
:
四、基尼指数

此概率的基尼分布指数为:
对于样本集A,其基尼指数为:


利用学历特征的决策值为“硕士”时划分样本集为两个子集,基尼指数为
五、代码:信息熵,信息增益,基尼指数计算(splitInfo.py)
# coding:UTF-8
import math
def sum_of_each_label(samples):
'''
统计样本集中每一类标签label出现的次数
para samples:list,样本的列表,每样本也是一个列表,样本的最后一项为label
retrurn sum_of_each_label:dictionary,各类样本的数量
'''
labels = [sample[-1] for sample in samples] #sample是相亲的一个人的个人信息,最后一个代表是否相亲成功
sum_of_each_label = dict([(i,labels.count(i)) for i in labels])#labels是列表,count(i)是计算i在列表labels里面出现的次数
return sum_of_each_label
#返回一个字典,
# 字典内容如 0->2,1->3,表示0出现2次,1出现3次
def info_entropy(samples):
'''
计算样本集的信息熵
para samples:list,样本的列表,每样本也是一个列表,样本的最后一项为label
return infoEntropy:float,样本集的信息熵
'''
# 统计每类标签的数量
label_counts = sum_of_each_label(samples)
# 计算信息熵 infoEntropy = -∑(p * log(p))
infoEntropy = 0.0
sumOfSamples = len(samples)
print('len(samples)=',len(samples))
for label in label_counts:
p = float(label_counts[label])/sumOfSamples
infoEntropy -= p * math.log(p,2)
return infoEntropy
def split_samples(samples, f, fvalue):
'''
切分样本集
para samples:list,样本的列表,每样本也是一个列表,样本的最后一项为label,其它项为特征
para f: int,切分的特征,用样本中的特征次序表示
para fvalue: float or int,切分特征的决策值
output lsamples: list, 切分后的左子集
output rsamples: list, 切分后的右子集
'''
lsamples = []
rsamples = []
for s in samples:#s是相亲的一个人的个人信息,f是切分特征
if s[f] < fvalue:
lsamples.append(s)
else:
rsamples.append(s)
return lsamples, rsamples
def info_gain(samples, f, fvalue):
'''
计算切分后的信息增益
para samples:list,样本的列表,每样本也是一个列表,样本的最后一项为label,其它项为特征
para f: int,切分的特征,用样本中的特征次序表示
para fvalue: float or int,切分特征的决策值
output : float, 切分后的信息增益
'''
lson, rson = split_samples(samples, f, fvalue)
return info_entropy(samples) - (info_entropy(lson)*len(lson) + info_entropy(rson)*len(rson))/len(samples)
def gini_index(samples):
'''
计算样本集的Gini指数
para samples:list,样本的列表,每样本也是一个列表,样本的最后一项为label,其它项为特征
output: float, 样本集的Gini指数
'''
sumOfSamples = len(samples)
if sumOfSamples == 0:
return 0
label_counts = sum_of_each_label(samples)
gini = 0
for label in label_counts:
gini = gini + pow(label_counts[label], 2)
return 1 - float(gini) / pow(sumOfSamples, 2)
def gini_index_splited(samples, f, fvalue):
'''
计算切分后的基尼指数
para samples:list,样本的列表,每样本也是一个列表,样本的最后一项为label,其它项为特征
para f: int,切分的特征,用样本中的特征次序表示
para fvalue: float or int,切分特征的决策值
output : float, 切分后的基尼指数
'''
lson, rson = split_samples(samples, f, fvalue)
return (gini_index(lson)*len(lson) + gini_index(rson)*len(rson))/len(samples)
if __name__ == "__main__":
# 表3-1 某人相亲数据,依次为年龄、身高、学历、月薪特征和是否相亲标签
blind_date = [[35, 176, 0, 20000, 0],
[28, 178, 1, 10000, 1],
[26, 172, 0, 25000, 0],
[29, 173, 2, 20000, 1],
[28, 174, 0, 15000, 1]]
# 计算集合的信息熵
print(info_entropy(blind_date))
# OUTPUT:0.9709505944546686
# 计算集合的信息增益
print(info_gain(blind_date,1,175)) # 按身高175切分
# OUTPUT:0.01997309402197478
print(info_gain(blind_date,2,1)) # 按学历是否硕士切分
# OUTPUT:0.4199730940219748
print(info_gain(blind_date,3,10000)) # 按月薪10000切分
# OUTPUT:0.0
# 计算集合的基尼指数
print(gini_index(blind_date))
# OUTPUT:0.48
# 计算切分后的基尼指数
print(gini_index_splited(blind_date,1,175)) # 按身高175切分
# OUTPUT:0.4666666666666667
print(gini_index_splited(blind_date,2,1)) # 按学历是否硕士切分
# OUTPUT:0.26666666666666666
print(gini_index_splited(blind_date,3,10000)) # 按月薪10000切分
# OUTPUT:0.48
print(gini_index_splited(blind_date,0,30)) # 按年龄30切分
# OUTPUT:0.3

![C/C++工业数据分析与文件信息管理系统[2023-02-12]](https://img-blog.csdnimg.cn/img_convert/086357f99012573e1a28840d77f5e1d7.png)
![[golang gin框架] 2.Gin HTML模板渲染以及模板语法,自定义模板函数,静态文件服务](https://img-blog.csdnimg.cn/img_convert/26e0c230782b5595d30ae31609607a05.png)