简单的密码加密

news2025/1/12 6:03:19

用户的密码必须被加密后再存储到数据库, 否则就存在用户账号安全问题

用户使用的原始密码通常称之为"原文"或"明文", 经过算法的运算, 得到的结果通常称之为"密文"

在处理密码加密时, 不可以使用任何加密算法, 因为所有加密算法都是可以被逆向运算的, 也就是说, 当密文、算法、加密参数作为已知条件的情况下, 是可以根据密文计算得到原文的

提示: 加密算法通常是用于保障数据传输过程的安全的, 并不适用于存储下来的数据的安全!

对存储的数据进行加密处理, 通常使用消息摘要算法

消息摘要算法的特点:

· 消息(原文、原始数据)相同, 则摘要相同

· 无论消息多长, 每个算法的摘要结果长度固定

· 消息不同, 则摘要极大概率不会相同

注意: 任何消息摘要算法都是不可逆向运算的算法! 即你永远不可能根据摘要(密文)逆向计算得到消息(原文)!

常见的消息摘要算法有:

· SHA系列: SHA-1、SHA-256、SHA-384、SHA-512

· MD家族: MD2、MD4、MD5

Spring框架内有DigestUtils的工具类, 提供了MD5的API, 例如:

package cn.tedu.csmall.product;

import org.junit.jupiter.api.Test;
import org.springframework.util.DigestUtils;

public class MessageDigestTests {

    @Test
    public void testMd5() {
        String rawPassword = "123456";
        String encodedPassword = DigestUtils
                .md5DigestAsHex(rawPassword.getBytes());
        System.out.println("原文：" + rawPassword);
        System.out.println("密文：" + encodedPassword);
        System.out.println();

        rawPassword = "123456";
        encodedPassword = DigestUtils
                .md5DigestAsHex(rawPassword.getBytes());
        System.out.println("原文：" + rawPassword);
        System.out.println("密文：" + encodedPassword);
        System.out.println();

        rawPassword = "1234567890ABCDEFGHIJKLMN";
        encodedPassword = DigestUtils
                .md5DigestAsHex(rawPassword.getBytes());
        System.out.println("原文：" + rawPassword);
        System.out.println("密文：" + encodedPassword);
    }

}

以上测试运行的结果为:

提示: 在项目中添加commons-codec的依赖项, 可以使用更多消息摘要算法的API

扩展

在算法的学术领域中, 如果算法的计算结果的长度是固定, 会根据结果是由多少位数二进制数来组成的方式来确定这是多少位的算法, 以MD5算法为例, 其计算结果是由128个二进制位数组成的, 所以, MD5算法是128位算法, 通常, 会将二进制结果转换成十六进制来表示, 所以会是32位长度的十六进制数!

常见的消息摘要算法中, MD系列的都是128位算法, SHA-1是160位算法, SHA-256是256位算法, SHA-384是384位算法, SHA-512是512位算法

理论上来说，如果某个消息摘要算法的结果只是1位（1个二进制数），最多使用2 + 1个不同的原文，必然发生“碰撞”（即完全不同的原文对应相同的摘要），同理，如果算法的结果有2位（2个二进制数组成），最多使用4 + 1个不同的原文必然后发生碰撞，如果算法的结果有3位，最多使用8 + 1个不同的原文必然发生碰撞，而MD5是128位算法，理论上，最多需要使用2的128次方 + 1个不同的原文才能保证必然发生碰撞！

2的128次方的值是：340282366920938463463374607431768211456。

当使用MD5处理密码加密时，理论上，需要尝试340282366920938463463374607431768211456 + 1个不同的原密码，才能试出2个不同的原密码都可以登录同一个账号！由于需要尝试的次数太多，按照目前的计算机的算力，这是不可能实现的！所以，大致可以视为“找不到2个不同的原文对应相同的结果”。

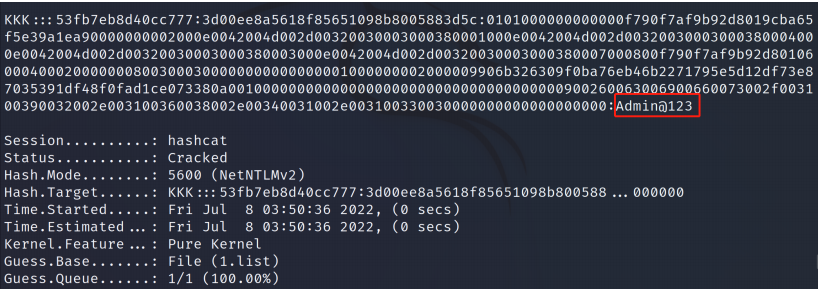
通过，对于使用消息摘要算法处理密码加密的结果，如果需要破解，只能尽可能的穷举原密码（消息/原文）与加密后的密码（摘要/密文）之间的对应关系，当执行“破解”时，从记录下来的结果中进行搜索即可！例如：