本篇文章讲述Java数据结构中关于二叉树相关知识及常见的二叉树OJ题做法讲解(包含非递归遍历二叉树)
目录
一、二叉树
1.1二叉树概念
1.2特殊的二叉树
1.3二叉树性质
1.4二叉树基本性质定理题
1.5二叉树遍历基本操作
1.6二叉树遍历的前中后非递归写法
1.7二叉树有关的基本操作
二、二叉树常见的OJ题
2.1相同的树
2.2对称二叉树
2.3反转二叉树
2.4二叉树的公共祖先
2.5二叉树的层序遍历
2.6根据二叉树前序与中序序列构造二叉树
一、二叉树
1.1二叉树概念
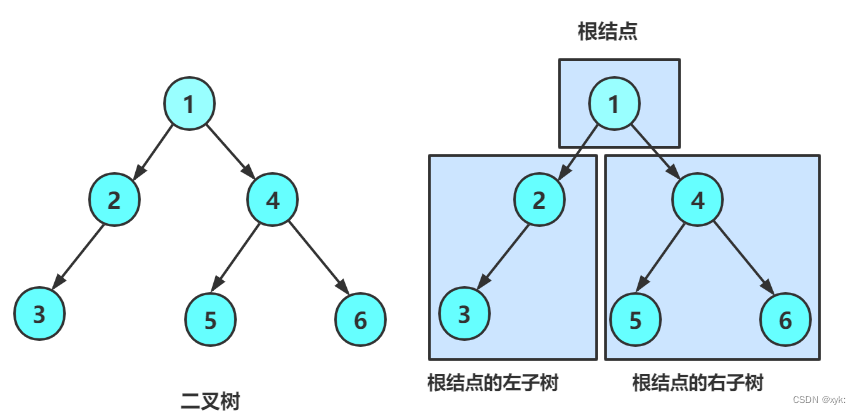
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。3. 二叉树不存在度大于2的结点
4. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树

1.2特殊的二叉树
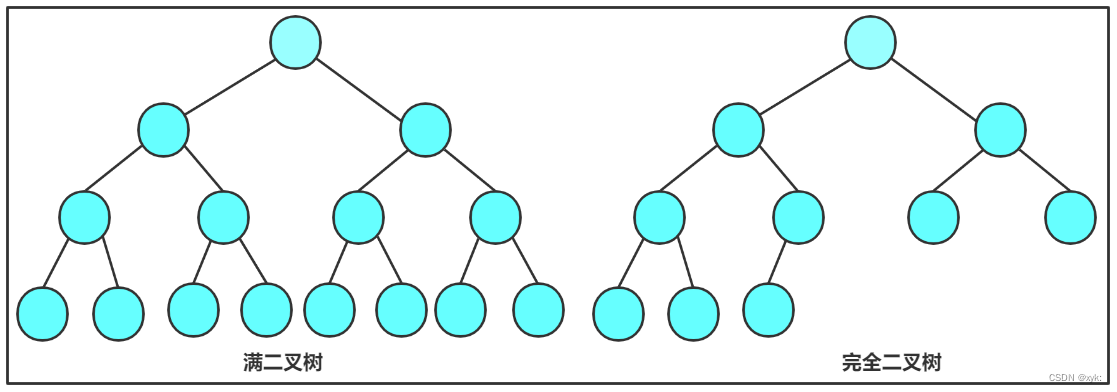
1. 满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
2. 完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
1.3二叉树性质
1. 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2^i-1 (i>0)个结点。
2. 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 2^k-1(k>=0)。
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1。
4. 具有n个结点的完全二叉树的深度k为log2(n+1)上取整。
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子
6.当完全二叉树有偶数个节点时,n1 = 1;
7.当完全二叉树有奇数个节点时,n1 = 0;
8.n层k叉树共有节点(k^n-1)/ (k-1);
1.4二叉树基本性质定理题
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( B)
A 不存在这样的二叉树
B 200
C 198
D 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )
A n
B n+1
C n-1
D n/23.一个具有767个节点的完全二叉树,其叶子节点个数为(B)
A 383
B 384
C 385
D 386
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为(B )
A 11
B 10
C 8
D 12
1.5二叉树遍历基本操作
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
- 代码实现:
- NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
- LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
- LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
public class TestBinaryTree {
static class TreeNode {
public char val;
public TreeNode left;//左孩子的引用
public TreeNode right;//右孩子的引用
public TreeNode(char val) {
this.val = val;
}
}
/**
* 创建一棵二叉树 返回这棵树的根节点
*
* @return
*/
public TreeNode createTree() {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
E.right = H;
//this.root = A;
return A;
}
// 前序遍历
public void preOrder(TreeNode root) {
if (root == null) {
return;
}
System.out.println(root.val + " ");
preOrder(root.left);
preOrder(root.right);
}
// 中序遍历
void inOrder(TreeNode root) {
if (root == null) {
return;
}
inOrder(root.left);
System.out.println(root.val + " ");
inOrder(root.right);
}
// 后序遍历
void postOrder(TreeNode root) {
if (root == null) {
return;
}
inOrder(root.left);
inOrder(root.right);
System.out.println(root.val + " ");
}1.6二叉树遍历的前中后非递归写法
//前序遍历非递归
public List<Integer> PreOrder(TreeNode root){
List<Integer> list = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()){
while (cur != null){
list.add(cur.val);
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
cur = cur.right;
}
return list;
}
//中序遍历非递归
public List<Integer> InorderTravelSal(TreeNode root){
if (root == null){
return new ArrayList<>();
}
List<Integer> list = new ArrayList<>();
LinkedList<TreeNode> stack = new LinkedList<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
list.add(cur.val);
cur = cur.right;
}
return list;
}
//后序遍历非递归
public List<Integer> PostOrder(TreeNode root){
if (root == null){
return new ArrayList<>();
}
List<Integer> list = new ArrayList<>();
Deque<TreeNode> stack = new LinkedList<>();
TreeNode cur = root;
TreeNode prev = null;
while (cur != null || !stack.isEmpty()){
while (cur != null){
stack.push(cur);
cur = cur.left;
}
TreeNode node = stack.peek();
if (node.right == null || node.right == prev){
list.add(node.val);
stack.pop();
prev = node;
}else {
cur = cur.right;
}
}
return list;
}1.7二叉树有关的基本操作
/**
* 获取树中节点的个数:遍历思路
*/
void size(TreeNode root) {
if (root == null) {
return;
}
nodeSize++;
size(root.left);
size(root.right);
}
/*
获取叶子节点的个数:子问题
*/
int getLeafNodeCount2(TreeNode root) {
if (root == null) {
return 0;
}
if (root.left == null && root.right == null) {
return 1;
}
int leftSize = getLeafNodeCount2(root.left);
int rightSize = getLeafNodeCount2(root.right);
return leftSize + rightSize;
}
/*
获取第K层节点的个数
*/
int getKLevelNodeCount(TreeNode root, int k) {
if (root == null) {
return 0;
}
if (k == 1) {
return 1;
}
int leftSize = getKLevelNodeCount(root.left, k - 1);
int rightSize = getKLevelNodeCount(root.right, k - 1);
return leftSize + rightSize;
}
/*
获取二叉树的高度
时间复杂度:O(N)
*/
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return (leftHeight > rightHeight) ?
(leftHeight + 1) : (rightHeight + 1);
}
// 检测值为value的元素是否存在
TreeNode find(TreeNode root, char val) {
if (root == null) {
return null;
}
if (root.val == val) {
return root;
}
TreeNode leftTree = find(root.left, val);
if (leftTree != null) {
return leftTree;
}
TreeNode rightTree = find(root.right, val);
if (rightTree != null) {
return rightTree;
}
return null;//没有找到
}二、二叉树常见的OJ题
2.1相同的树
100. 相同的树 - 力扣(LeetCode)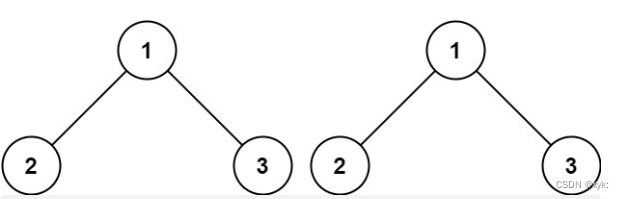
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p == null && q == null){
return true;
}
if(p != null && q == null || p == null && q != null){
return false;
}
if(p.val != q.val){
return false;
}
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
}2.2对称二叉树
101. 对称二叉树 - 力扣(LeetCode)
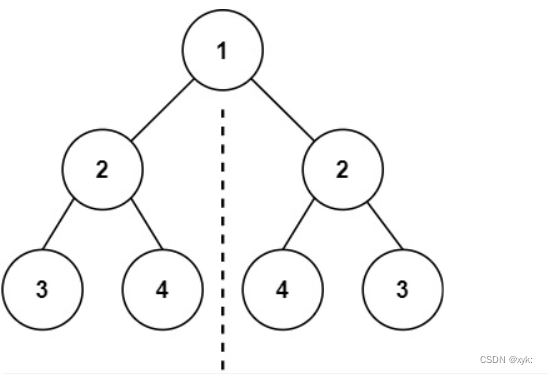
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null){return true;}
return isSymmetricChild(root.left,root.right);
}
public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){
if (leftTree != null && rightTree == null ||
leftTree == null && rightTree != null){
return false;
}
if (leftTree == null && rightTree == null){
return true;
}
if (leftTree.val != rightTree.val){
return false;
}
return isSymmetricChild(leftTree.left,rightTree.right) &&
isSymmetricChild(leftTree.right,rightTree.left);
}
}与上一道相同的树原理一致。
2.3反转二叉树
226. 翻转二叉树 - 力扣(LeetCode)
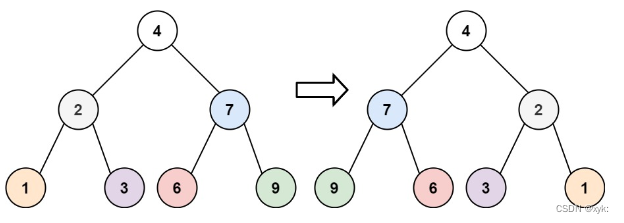
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null){
return null;
}
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
invertTree(root.left);
invertTree(root.right);
return root;
}
}注意将子节点的每个节点都要反转
2.4二叉树的公共祖先
最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)
236. 二叉树的最近公共祖先 - 力扣(LeetCode)
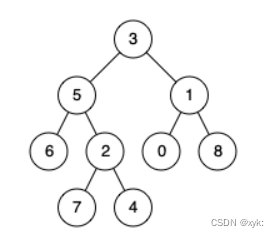
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null){
return null;
}
if(root == q || root == p){
return root;
}
TreeNode leftRet = lowestCommonAncestor(root.left,p,q);
TreeNode rightRet = lowestCommonAncestor(root.right,p,q);
if(leftRet != null && rightRet != null){
return root;
}else if(leftRet != null){
return leftRet;
}else if(rightRet != null){
return rightRet;
}
return null;
}
}注意在左右子树中寻找节点,如果找到并返回节点,否则返回空
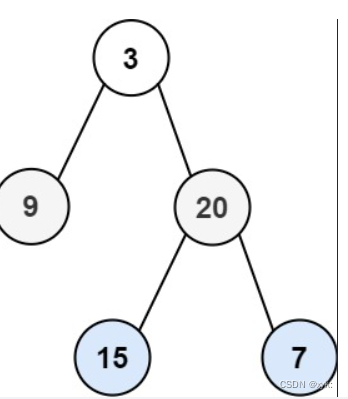
2.5二叉树的层序遍历
102. 二叉树的层序遍历 - 力扣(LeetCode)
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> list = new ArrayList<>();
if (root == null) {
return list;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
List<Integer> tmp = new ArrayList<>();
while (size > 0) {
TreeNode cur = queue.poll();
tmp.add((int) cur.val);
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
size--;
}
list.add(tmp);
}
return list;
}
}本题需要注意层序遍历要使用队列,先进先出。
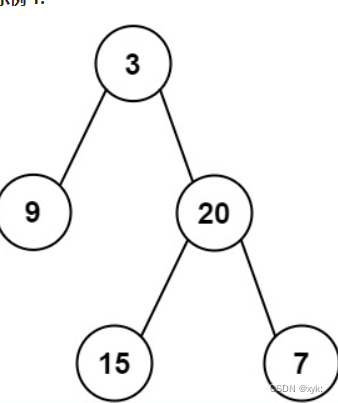
2.6根据二叉树前序与中序序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return buildTreechild(preorder,inorder,0,inorder.length-1);
}
int i = 0;
public TreeNode buildTreechild(int[] preorder,int[] inorder,int inbegin,int inend){
if(inbegin > inend){
return null;
}
TreeNode root = new TreeNode(preorder[i]);
int rootIndex = findIndex(inorder,inbegin,inend,preorder[i]);
i++;
root.left = buildTreechild(preorder,inorder,inbegin,rootIndex-1);
root.right = buildTreechild(preorder,inorder,rootIndex+1,inend);
return root;
}
public int findIndex(int[] inorder,int inbegin,int inend,int key){
for(int i = inbegin;i <= inend;i++){
if(inorder[i]==key){
return i;
}
}
return -1;
}
}本题需要注意的点是只有给出前序或后续序列才能确定中序中根的位置