目录
题目描述
输入描述
输出描述
用例
题目解析
算法源码
题目描述
现在有一队小朋友,他们高矮不同,我们以正整数数组表示这一队小朋友的身高,如数组{5,3,1,2,3}。
我们现在希望小朋友排队,以“高”“矮”“高”“矮”顺序排列,每一个“高”位置的小朋友要比相邻的位置高或者相等;每一个“矮”位置的小朋友要比相邻的位置矮或者相等;
要求小朋友们移动的距离和最小,第一个从“高”位开始排,输出最小移动距离即可。
例如,在示范小队{5,3,1,2,3}中,{5, 1, 3, 2, 3}是排序结果。
{5, 2, 3, 1, 3} 虽然也满足“高”“矮”“高”“矮”顺序排列,但小朋友们的移动距离大,所以不是最优结果。
移动距离的定义如下所示:
第二位小朋友移到第三位小朋友后面,移动距离为1,若移动到第四位小朋友后面,移动距离为2;
输入描述
排序前的小朋友,以英文空格的正整数:
4 3 5 7 8
注:小朋友<100个
输出描述
排序后的小朋友,以英文空格分割的正整数:4 3 7 5 8
备注:4(高)3(矮)7(高)5(矮)8(高), 输出结果为最小移动距离,只有5和7交换了位置,移动距离都是1。
用例
| 输入 | 4 1 3 5 2 |
| 输出 | 4 1 5 2 3 |
| 说明 | 无 |
| 输入 | 1 1 1 1 1 |
| 输出 | 1 1 1 1 1 |
| 说明 | 相邻位置可以相等 |
| 输入 | xxx |
| 输出 | [ ] |
| 说明 | 出现非法参数情况, 返回空数组。 |
题目解析
感觉本题的用例1是存在问题的
4 1 3 5 2
的最小移动距离应该是1,即让5和2交换位置,变为:4 1 3 2 5,这样的话,也满足:高 矮 高 矮 高。
而用例输出的逻辑是先让3和5交换,变为 4 1 5 3 2,再让3和2交换,变为 4 1 5 2 3,这样的话也满足:高 矮 高 矮 高,但是却交换了两次,也就是说移动距离是2。
难道说,用例逻辑是,必须要从第一个小朋友开始,每当遇到不符合要求的排队顺序,就必须交换位置吗?
那么题目描述中又为何要强调最小距离呢?
感觉这题有点自相矛盾。
我这里按照符合用例要求的逻辑写的代码,示意图如下
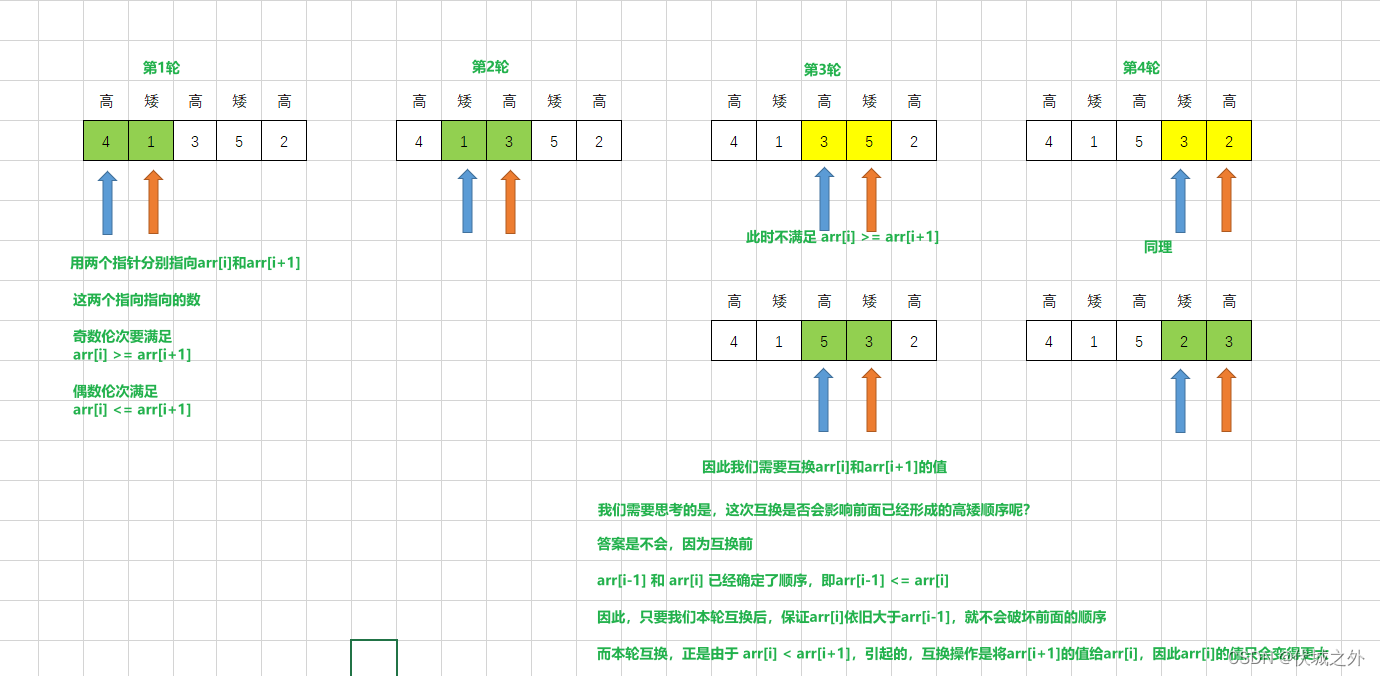
但是这种算法是不满足最小距离要求的。
算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
if (!/(\d\s)+/.test(line)) return console.log("[]");
const arr = line.split(" ").map(Number);
let flag = true;
for (let i = 0; i < arr.length - 1; i++) {
if (arr[i] !== arr[i + 1] && arr[i] > arr[i + 1] !== flag) {
let tmp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = tmp;
}
flag = !flag;
}
console.log(arr.join(" "));
});