算法笔记(五)
排序算法
- 算法笔记(五)
- 前言
- 一、冒泡排序
- 1.什么是冒泡排序
- 2.实际需求
- 3.代码实现
- 二、选择排序
- 1.什么是选择排序
- 2.需求规则
- 三.插入排序
- 1.了解插入排序
- 2.需求规则
- 3.代码实现
- 四.希尔排序
- 1.什么是希尔排序
- 2.需求规则
- 3.代码实现
- 五.快速排序
- 1.什么是快速排序
- 2.需求规则
- 3.代码演示
- 六.归并排序
- 1.什么是归并排序
- 2.需求规则
- 3.代码展示
- 总结
前言
基础数据结构告一段落,现在开始一起学习排序算法
一、冒泡排序
1.什么是冒泡排序
冒泡排序(Bubble Sor)是把一组数据从左边开始进行两两比较交换,小的放前面,大的放后面,通过反复比较一直到没有数据需要交换为止。该排序方法由于很像水里的泡泡,从水底冒出的小泡泡升到水面变成大的,体现了从小到大的排序过程(如图所示)。

2.实际需求
(1)从队首开始,两两比较数值,把大的往后交换,一直到队尾,第一个最大值固定到最后。
(2)再从队首开始,依次两两比较,把次最大放到倒数第二位置。
(3)依次循环比较,直到完成所有数的比较和交换,完成冒泡排序。
人工图示演示
第一步,1=[9,0,6,5,3,10,36,2,1]列表传入自定义函数bubblesort(), n=9。
第二步,i=0, j=0, s:[0]=9, s[1]=0, s[0]>s[1]为真, 则把0放前面9放后面;然后,9与6进行比较,6放前面9放后面; 9与5比较,5放前面9放后面; 9与3比较,3放前面9放后面;9与10比较,无须交换; 10 与36比较,无须交换位置; 36 与2比较,2放前面36放后面; 36与1比较,1放前面36放最后。第一次循环比较结果如图4.2所示,最大的数36放到了最后。
第三步,i=1,j=0, s:[0]-0, s:[1]=6,0与6比较,无须交换位置: 6与5比较,5放前面6放后面: 6与3比较,3放前面6放后面; 6与9比较,无须交换位置: 9与10比较,无须交换位置:10与2比较,2放前面10放后面: 10与1比较,1放前面10放后面。第二次循环结束,如图所示。

3.代码实现
def bubblesort(s1):
n = len(s1)
for i in range(n): # 冒泡循环次数控制
for j in range(n - i - 1): # 冒泡循环一次,范围往前面缩1
if s1[j] > s1[j + 1]:
c1 = s1[j] # 把大的赋给c1
s1[j] = s1[j + 1] # 把小的换到前一位
s1[j + 1] = c1 # 把c1赋给后一位
l1 = [9, 0, 6, 5, 3, 10, 36, 2, 1]
print("排序之前的顺序", l1)
bubblesort(l1)
print("排序之后的顺序", l1)
运行结果

二、选择排序
1.什么是选择排序
选择排序是另外一一种简单的排序 方法。在数据集合里,通过轮循环找到最小值,把它放到第一个位置,然后在剩余的数据中再我最小值,放到第二个位置。以此类推,直到将所有值排序完成。
2.需求规则
(1)输入n个数值的列表,开始0到n-1轮的循环。
(2) 每轮循环记住最小值的下标,当前循环结束, 把最小值放到最前面。
(3)接着进行下一 轮循环,把最小值下标进行标记, 最后把最小值放到当前轮循环开始的位置。
(4)一直到第n-1轮,结束所有最小值的选择。
人工图示
第一步,把列表s1传入SeletSor(arr)自定义函数。
第二步 i = 0到5, j=i到S进行循环,每循环一次选择一个最小值,放到循环的最前面,循环比较过程如图

def selectsort(s1):
n = len(s1)
if n == 1:
return 1
for i in range(n):
mid = i # 获得每次循环第一个比较值的下标
for j in range(i, n - 1): # 每次循环里寻找最小值
if s1[mid] > s1[j + 1]: # 循环过程判断最小值
mid += 1 # 获得更小值的下标
s1[i], s1[mid] = s1[mid], s1[i] # 把最小的放到最前面
s1 = [3, 18, 0, 32, 2, 1]
print("排序之前:", s1)
selectsort(s1)
print("排序之后:", s1)
运行结果

三.插入排序
1.了解插入排序
插入排序(Insertion Sort)的原理是数列前而为排序完成的值,数列后面为未排序的值。取已
排序的值右边第一个 未排序的值CI,与已经排序的值进行比较,当C1大于当前值时,把当前值向后
移动1位,继续往前比较,当c小于当前值时,在当前位置插入Ci并把当前值向后移动1位,
完成一个循环的插入比较。接着进行下一轮的循环插入比较,一直 到所有未排序的值都完成插入
操作。第一次循环时,可以把数列第一。个值作为已经排序的数来看待,从第二个值开始进行插入
操作。
2.需求规则
(1)输入n个数值的列表。
2)先进行下标是0和1的数值比较,把大的放后面,小的插入前面,第1轮插入比较结束。
(3)继续选择下标是2的数值和下标是1的数值进行比较,大的后移1位,小的放到临时变量c中;然后继续比较c1和下标是0的数值,大的后移1位,小的插入前面。
(4)依次比较插入,一直到n-1轮结束比较, 获得最终排序结果。
人工图示演示

3.代码实现
def insertsort(arr):
n = len(arr)
if n == 1:
return 1
for i in range(1, n):
c1 = arr[i]
j = i
while j > 0 and c1 < arr[j - 1]:
arr[j] = arr[j - 1]
j -= 1
arr[j] = c1
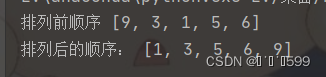
l2 = [9, 3, 1, 5, 6]
print("排列前顺序", l2)
insertsort(l2)
print("排列后的顺序:", l2)
运行结果
四.希尔排序
1.什么是希尔排序
希尔排序(Sel Sor)又叫作缩小增量排序算法,是插入排序的一种更高效的改进算法。
2.需求规则
希尔排序的基本思想是:在n个元素的数列里,取增量spcn/数列开始值和增量尾值之间进行比较,小的放前面,大的放后面:把增量前后的数值都比较一遍, 然后增量数space减1,继续从头到尾做比较,并调整大小;一直到space=1,就完成了所有元素的大小调整和排序。
增量space的取法有各种方案。最初Shell提出取space=n//2向下取整,space =space//2 向下取整,直到increment=1。但由于直到最后一步,奇数位置的元素才会与偶数位置的元素进行比较,这祥使用这个序列的效率会很低。后来Knuth提出取spacen/3向下取整+1,还有人提出都取奇数也有人提出space互质。使用不同的序列会使希尔排序算法的性能有很大的差异。
人工演示图
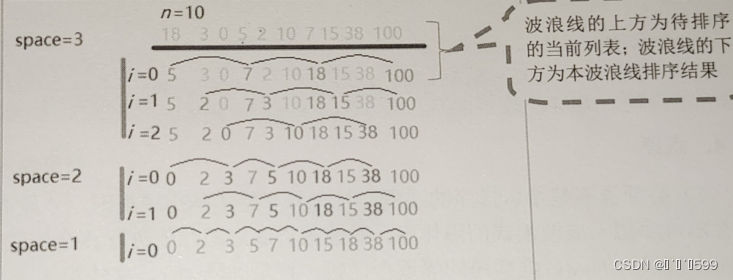
3.代码实现
def sellsort(arr):
n = len(arr)
endi = 0 # 最后修改下标
if n == 1:
return 1
space = n // 3 # 以列表中1/3作为增量
while space > 0:
for i in range(space): # 控制一个变量循环space次
key = arr[i]
j = 0 # 控制每个key元素在列表里比较次数
while i + (j + 1) * space < n:
print(f'交换开始下标数{j},交换结束{i + (j + 1) * space}')
if space > 1:
if arr[i + (j + 1) * space] < key:
arr[i + j * space] = arr[i + (j + 1) * space]
endi = i + (j + 1) * space
else: # 当增量为1时,相邻元素比较并调整
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
j += 1
if arr[i] != key: # 必须考虑无需交换情况
arr[endi] = key
space -= 1
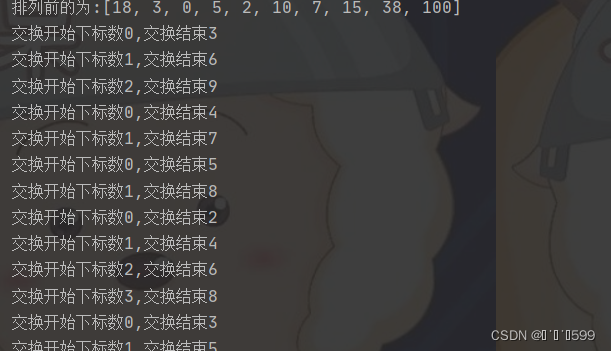
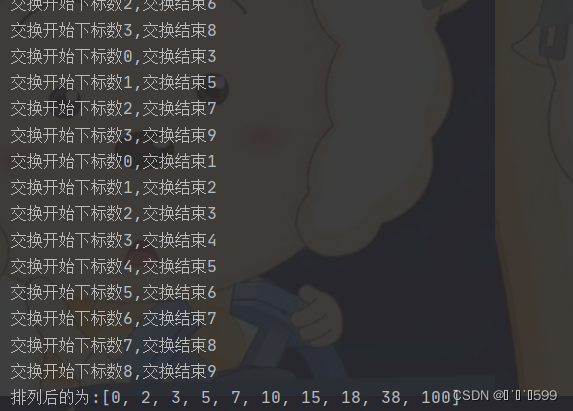
s1 = [18, 3, 0, 5, 2, 10, 7, 15, 38, 100]
print(f"排列前的为:{s1}")
sellsort(s1)
print(f"排列后的为:{s1}")
运行结果
五.快速排序
1.什么是快速排序
快速排序(Quick Sort)是对冒泡排序的一种改进, 由C.A.R.Hoare在1960年提出。它的基本思想是:通过一轮排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,直到整个数据变成有序序列。分割时,先选择一个元素作 为比较大小的基准(Pivot) 数。把数列里小于Pivot 数的元素放到前面,大于Pivot数的元素放到后面。这个基准数可以任意取一一个, 一般取开始、结束或中间位置的一个元素。
由于该算法需要把不同部分的两部分数据迭代缩小排序,所以采用了递归排序方法,通过空间换时间,实现快速排序。
2.需求规则
(1)选取列表最后一个数值作为基准数P, 把比P小的数放前面, 比P大的数放后面。
(2)分别对前面部分和后面部分的数据按照(1)的原则进行排列。
(3)一直到每部分的下标low==high,完成快速排序。
图示演示

3.代码演示
def movepivot(arr, low, hight):
pivot = arr[hight]
imove = (low - 1)
for i in range(low, hight):
if arr[i] <= pivot:
imove += 1
arr[imove], arr[i] = arr[i], arr[imove]
arr[imove + 1], arr[hight] = arr[hight], arr[imove + 1]
return imove + 1
def quicksort(arr, low, hight):
if low < hight:
pivot = movepivot(arr, low, hight)
quicksort(arr, low, pivot - 1)
quicksort(arr, pivot + 1, hight)
s1 = [10, 3, 28, 4, 12, 20]
print(f"排序前{s1}")
h = len(s1)
quicksort(s1, 0, h - 1)
print(f"排序后的结果{s1}")
结果如下

六.归并排序
1.什么是归并排序
归并排序(Merge Sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
2.需求规则
分治法先把数列分成相对均衡的两部分n/2,
然后再把左边的(eft) 子数列和右边的(right)
的子数列再各分成两部分:继续如此等分,直到只有一个元素。
等分过程采用递归方法,每分次, 在内存开辟临时的记录区域。所有元素分完后,开始大小比较归并,从两个元素比较归并到n/比较归并。
s1=[1,9,10,4,50,6,7,90,21,23,45],其数量长度为n=11
第一次分割, n//2=5,通过递归,把左边left[:5]存储到临时空间,右边right[:5]也如此。
第二次分制,把左边lelt[:5]分别为 left1[:2]、right1[2:] 右边right[5:]分割为left2[:7]、right2[7:]
第三次分割,在第二次分割的基础上再分别递归分割。
第四次分割,完成了所有元素的分割,分割为最小单元1.
接下来对分割完成的各个数列进行并归排序操作。
第一次并归,分别完成1和9的比较合并、4和50的比较合并,在前面合并的基础上生成了1、9、10、4、50子数组;同时完成了7和90比较合并、23和45比较合并。
第二次并归,实现了1、4、9、10、50的比较和并归,6、7、21、23、45、90的比较和并归。
第三次并归,实现了1、4、6、7、9、10、21、23、45、50、90所有元素的最终排序过程。
图示演示

3.代码展示
def mergesort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = mergesort(arr[:mid])
right = mergesort(arr[mid:])
return merge(left, right)
def merge(left, right):
r, l = 0, 0
temp = []
lmax = len(left)
rmax = len(right)
while l < lmax and r < rmax:
if left[l] <= right[r]:
temp.append(left[l])
l += 1
else:
temp.append(right[r])
r += 1
temp += list(left[l:])
temp += list(right[r:])
return temp
s1 = [1,9,10,4,50,6,7,90,21,23,45]
print(f"排列之前为{s1}")
print(f"排列之后为{mergesort(s1)}")
运行结果如下

总结
到此,排序算法就结束了,大家可以点击这里一起探讨吧,下章将带上检索算法的笔记