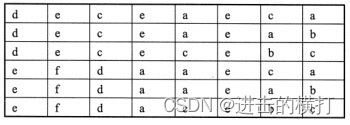
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/search-a-2d-matrix-ii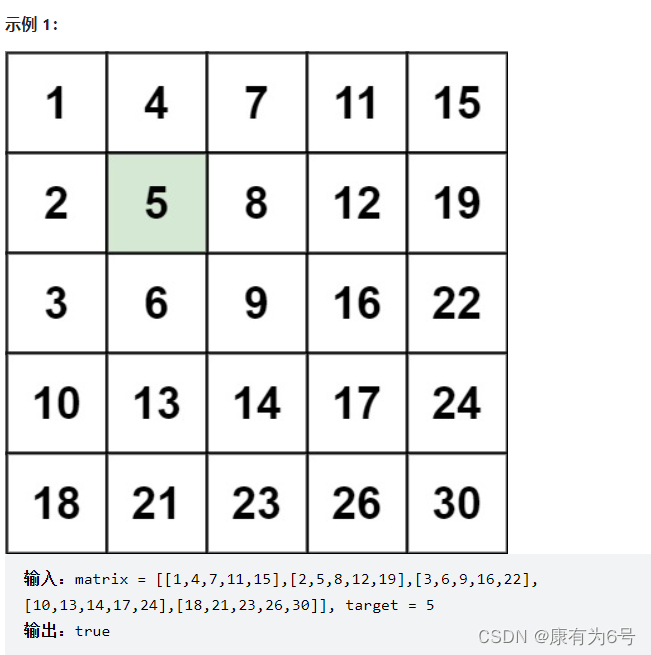

 

方法1：暴力搜索

非常不好的方法，无脑搜

遍历整个二维数组去搜索

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        for (int[] row : matrix) {
            for (int element : row) {
                if (element == target) {
                    return true;
                }
            }
        }
        return false;
    }
}

可以看出效果不好 

方法2：二分搜索

由于矩阵matrix 中每一行的元素都是升序排列的，因此我们可以对每一行都使用一次二分查找，判断 target 是否在该行中，从而判断target 是否出现。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        for (int[] row : matrix) {
            int index = search(row, target);
            if (index >= 0) {
                return true;
            }
        }
        return false;
    }

    public int search(int[] nums, int target) {
        int low = 0, high = nums.length - 1;
        while (low <= high) {
            int mid = (high - low) / 2 + low;
            int num = nums[mid];
            if (num == target) {
                return mid;
            } else if (num > target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return -1;
    }
}

效果有所提高，但还是太好 

方法3：二分搜索优化

在对每一行进行二分搜索之前，先进行判断：

1.如果这一行的头比目标值大，那这一行不可能有目标值，下面几行也不可能有，直接false

2.如果这一行的尾比目标值小，那这一行不可能有目标值，去下面几行找

加上上面的这两个判断，程序的时间复杂度会优化很多

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        for (int i = 0; i < m; i++) {
            //头不能比target大
            if (matrix[i][0] > target){
                return false;
            }
            //尾不能比target小
            if (matrix[i][n-1] < target)continue;
            //合适的就二分搜索
            int left = 0;
            int right = n-1;

            while (true){
                int middle = (left+right)/2;
                if (target == matrix[i][middle])return true;
                else if (target > matrix[i][middle]){
                    left = middle;
                }else if (target < matrix[i][middle]){
                    right = middle;
                }
                if (left+1 == right){
                    if (target == matrix[i][left] || target == matrix[i][right])return true;
                    else break;
                }
            }

        }
        return false;
    }
}

不错，优化了很多