目录
1 知识一网打尽
2 蚂蚁狮子优化算法在电力系统经济调度中的应用
3 运行结果
4 Matlab代码实现

1 知识一网打尽
这里总结一位博主的电力系统经济调度目录
| 蚂蚁狮子优化算法(完整Matlab代码实现) |
| 多目标蚂蚁狮子优化算法(Matlab代码实现) |
| 粒子群算法求解电力系统环境经济调度+微电网调度(风、光、电动车、柴油机、主网)(Python代码实现) |
| 改进的多目标差分进化算法在电力系统环境经济调度中的应用(Python代码实现)【电气期刊论文复现】 |
| 多目标灰太狼算法求解环境经济调度问题(IEEE30)(Matlab实现) |
| 改进粒子群算法求解电力系统经济调度问题(Matlab实现) |
| 多元宇宙算法求解电力系统多目标优化问题(Matlab实现)【电气期刊论文复现】 |
2 蚂蚁狮子优化算法在电力系统经济调度中的应用
蚁狮或所谓的涂鸦虫是蚁蛉科家族的成员,属于神经翅目(网翅昆虫)。蚁狮的生命有两个关键阶段:幼虫和成虫。成年期仅持续 3-5 周,用于繁殖。另一方面,生命周期的延长阶段,即幼虫阶段,大部分用于猎杀他们最喜欢的猎物,即蚂蚁。蚁狮幼虫的狩猎行为独特而迷人。如图1所示,是蚂蚁狮子和它的狩猎机制。

它们沿着圆形路径移动,并用它们巨大的下颚扔出沙子,在沙质土壤中形成小的(1-3 英寸长)漏斗形坑,如图2所示,以诱捕蚂蚁。

他们躲在坑底下,等待蚂蚁或小昆虫被困。漏斗形坑的边缘非常锋利,小昆虫无法逃脱,很容易掉到陷阱底部,如图3所示。蚁狮还不断将沙子扔向陷阱的外缘,以阻止猎物的任何逃跑尝试。

最后,昆虫滑入坑底,被拉到土壤下并被蚁狮吃掉。猎物的残骸被扔到坑外。之后,蚁狮为后续的目标猎物修改坑。蚁狮的饥饿程度越高,它们挖的陷阱就越大。通过这种方式,蚁狮已经进化和调整,以提高它们的生存前景。
详细的数学模型见第一部分的知识一网打尽。
部分代码:
clc;
clear;
close all;
warning off;
%% 基于MOALO求解具有阀点效应的环境经济调度问题
% 数有 5 列数据分别为燃料成本系数a,b,c和发电机组上下限约束。
% 1.a ($/MW^2) 2. b $/MW 3. c ($) 4.机组下限(MW) 5.机组上限(MW)
%行数表示发电机台数(n)
data=[0.007 7 240 100 500
0.0095 10 200 50 200
0.009 8.5 220 80 300
0.009 11 200 50 150
0.008 10.5 220 50 200
0.0075 12 120 50 120];
%% 网损系数
B=1e-4*[0.14 0.17 0.15 0.19 0.26 0.22
0.17 0.6 0.13 0.16 0.15 0.2
0.15 0.13 0.65 0.17 0.24 0.19
0.19 0.16 0.17 0.71 0.3 0.25
0.26 0.15 0.24 0.3 0.69 0.32
0.22 0.2 0.19 0.25 0.32 0.85
];
%% 负荷需求(MW)
Pd=700;
%% 目标函数
ObjectiveFunction=@eldnba; %调用目标函数
dim=length(data(:,1));
lb=0;
ub=1;
obj_no=1;
if size(ub,2)==1
ub=ones(1,dim)*ub;
lb=ones(1,dim)*lb;
end
%% 初始化蚁狮优化算法参数
max_iter=100;
N=100;
ArchiveMaxSize=100;
Archive_X=zeros(100,dim);
Archive_F=ones(100,obj_no)*inf;
Archive_member_no=0;
r=(ub-lb)/2;
V_max=(ub(1)-lb(1))/10;
Elite_fitness=inf*ones(1,obj_no);
Elite_position=zeros(dim,1);
Ant_Position=initialization(N,dim,ub,lb);
fitness=zeros(N,2);
V=initialization(N,dim,ub,lb);
iter=0;
position_history=zeros(N,max_iter,dim);
for iter=1:max_iter
for i=1:N %首先计算所有的目标值
Particles_F(i,:)=ObjectiveFunction(Ant_Position(:,i)');
if dominates(Particles_F(i,:),Elite_fitness)
Elite_fitness=Particles_F(i,:);
Elite_position=Ant_Position(:,i);
end
end
[Archive_X, Archive_F, Archive_member_no]=UpdateArchive(Archive_X, Archive_F, Ant_Position, Particles_F, Archive_member_no);
if Archive_member_no>ArchiveMaxSize
Archive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);
[Archive_X, Archive_F, Archive_mem_ranks, Archive_member_no]=HandleFullArchive(Archive_X, Archive_F, Archive_member_no, Archive_mem_ranks, ArchiveMaxSize);
else
Archive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);
end
Archive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);
index=RouletteWheelSelection(1./(Archive_mem_ranks+1e-20));
if index==-1
index=1;
end
Elite_fitness=Archive_F(index,:);
Elite_position=Archive_X(index,:)';
Random_antlion_fitness=Archive_F(1,:);
Random_antlion_position=Archive_X(1,:)';
for i=1:N
index=0;
neighbours_no=0;
RA=Random_walk_around_antlion(dim,max_iter,lb,ub, Random_antlion_position',iter);
[RE]=Random_walk_around_antlion(dim,max_iter,lb,ub, Elite_position',iter);
Ant_Position(:,i)=(RE(iter,:)'+RA(iter,:)')/2;
Flag4ub=Ant_Position(:,i)>ub';
Flag4lb=Ant_Position(:,i)<lb';
Ant_Position(:,i)=(Ant_Position(:,i).*(~(Flag4ub+Flag4lb)))+ub'.*Flag4ub+lb'.*Flag4lb;
end
display(['在迭代时 ', num2str(iter), ', ', num2str(Archive_member_no), ' 非支配解决方案为']);
K(iter)=Elite_fitness;
end
[F P Pl]=eldnba(Elite_position)
plot(K)
grid
title('迭代次数与最佳函数值');
xlabel('迭代次数')
ylabel('函数值')
clc;
clear;
close all;
warning off;
%% 基于MOALO求解具有阀点效应的环境经济调度问题
% 数有 5 列数据分别为燃料成本系数a,b,c和发电机组上下限约束。
% 1.a ($/MW^2) 2. b $/MW 3. c ($) 4.机组下限(MW) 5.机组上限(MW)
%行数表示发电机台数(n)
data=[0.007 7 240 100 500
0.0095 10 200 50 200
0.009 8.5 220 80 300
0.009 11 200 50 150
0.008 10.5 220 50 200
0.0075 12 120 50 120];
%% 网损系数
B=1e-4*[0.14 0.17 0.15 0.19 0.26 0.22
0.17 0.6 0.13 0.16 0.15 0.2
0.15 0.13 0.65 0.17 0.24 0.19
0.19 0.16 0.17 0.71 0.3 0.25
0.26 0.15 0.24 0.3 0.69 0.32
0.22 0.2 0.19 0.25 0.32 0.85
];
%% 负荷需求(MW)
Pd=700;
%% 目标函数
ObjectiveFunction=@eldnba; %调用目标函数
dim=length(data(:,1));
lb=0;
ub=1;
obj_no=1;
if size(ub,2)==1
ub=ones(1,dim)*ub;
lb=ones(1,dim)*lb;
end
%% 初始化蚁狮优化算法参数
max_iter=100;
N=100;
ArchiveMaxSize=100;
Archive_X=zeros(100,dim);
Archive_F=ones(100,obj_no)*inf;
Archive_member_no=0;
r=(ub-lb)/2;
V_max=(ub(1)-lb(1))/10;
Elite_fitness=inf*ones(1,obj_no);
Elite_position=zeros(dim,1);
Ant_Position=initialization(N,dim,ub,lb);
fitness=zeros(N,2);
V=initialization(N,dim,ub,lb);
iter=0;
position_history=zeros(N,max_iter,dim);
for iter=1:max_iter
for i=1:N %首先计算所有的目标值
Particles_F(i,:)=ObjectiveFunction(Ant_Position(:,i)');
if dominates(Particles_F(i,:),Elite_fitness)
Elite_fitness=Particles_F(i,:);
Elite_position=Ant_Position(:,i);
end
end
[Archive_X, Archive_F, Archive_member_no]=UpdateArchive(Archive_X, Archive_F, Ant_Position, Particles_F, Archive_member_no);
if Archive_member_no>ArchiveMaxSize
Archive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);
[Archive_X, Archive_F, Archive_mem_ranks, Archive_member_no]=HandleFullArchive(Archive_X, Archive_F, Archive_member_no, Archive_mem_ranks, ArchiveMaxSize);
else
Archive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);
end
Archive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);
index=RouletteWheelSelection(1./(Archive_mem_ranks+1e-20));
if index==-1
index=1;
end
Elite_fitness=Archive_F(index,:);
Elite_position=Archive_X(index,:)';
Random_antlion_fitness=Archive_F(1,:);
Random_antlion_position=Archive_X(1,:)';
for i=1:N
index=0;
neighbours_no=0;
RA=Random_walk_around_antlion(dim,max_iter,lb,ub, Random_antlion_position',iter);
[RE]=Random_walk_around_antlion(dim,max_iter,lb,ub, Elite_position',iter);
Ant_Position(:,i)=(RE(iter,:)'+RA(iter,:)')/2;
Flag4ub=Ant_Position(:,i)>ub';
Flag4lb=Ant_Position(:,i)<lb';
Ant_Position(:,i)=(Ant_Position(:,i).*(~(Flag4ub+Flag4lb)))+ub'.*Flag4ub+lb'.*Flag4lb;
end
display(['在迭代时 ', num2str(iter), ', ', num2str(Archive_member_no), ' 非支配解决方案为']);
K(iter)=Elite_fitness;
end
[F P Pl]=eldnba(Elite_position)
plot(K)
grid
title('迭代次数与最佳函数值');
xlabel('迭代次数')
ylabel('函数值')
完整代码:评论区回复关键字
3 运行结果
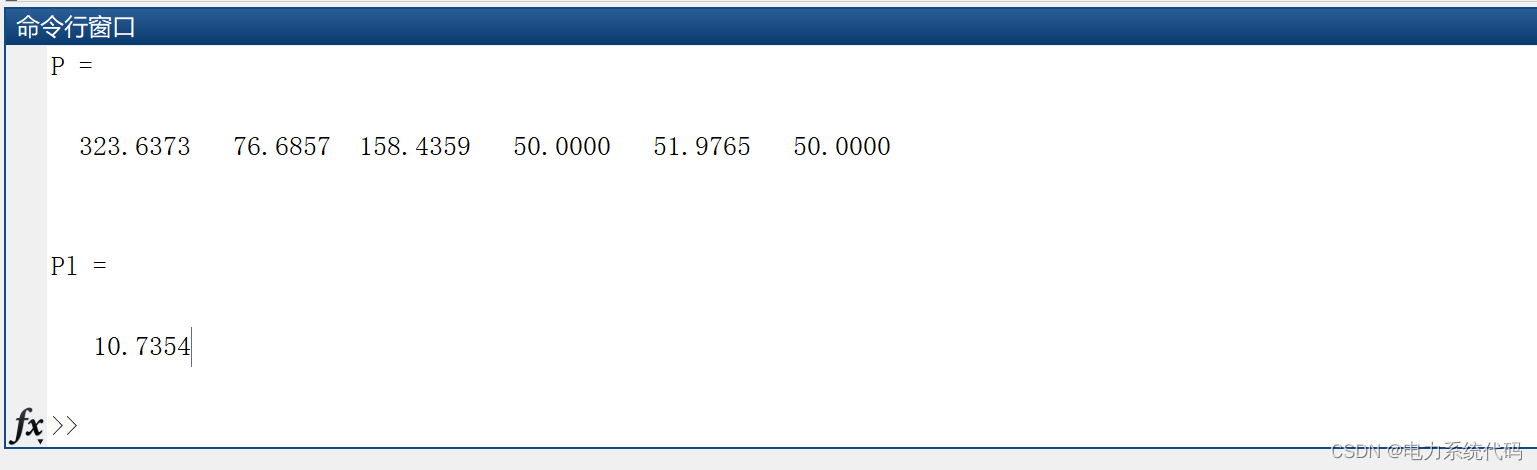


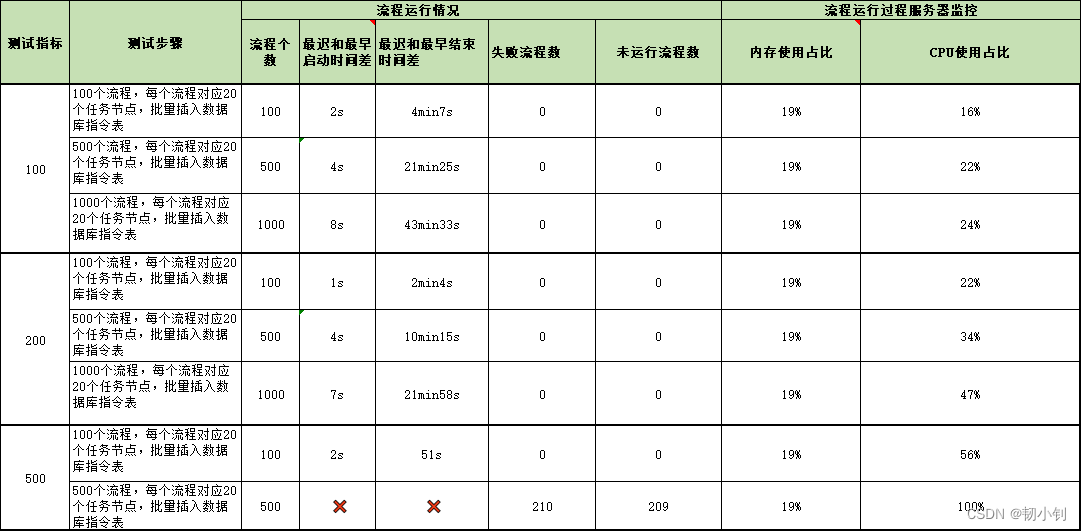





![[附源码]Python计算机毕业设计出版社样书申请管理系统](https://img-blog.csdnimg.cn/52e37ea1aaa44fb79b9fdcc135c11ebb.png)
