我们给出了一个(轴对齐的)二维矩形列表 rectangles 。 对于 rectangle[i] = [xi1, yi1, xi2, yi2], 表示第 i 个矩形的坐标, (xi1, yi1) 是该矩形 左下角 的坐标, (xi2, yi2) 是该矩形 右上角 的坐标。
计算平面中所有 rectangles 所覆盖的总面积 。任何被两个或多个矩形覆盖的区域应只计算 一次 。
返回 总面积 。因为答案可能太大,返回 109 + 7 的 模 。
示例 1:
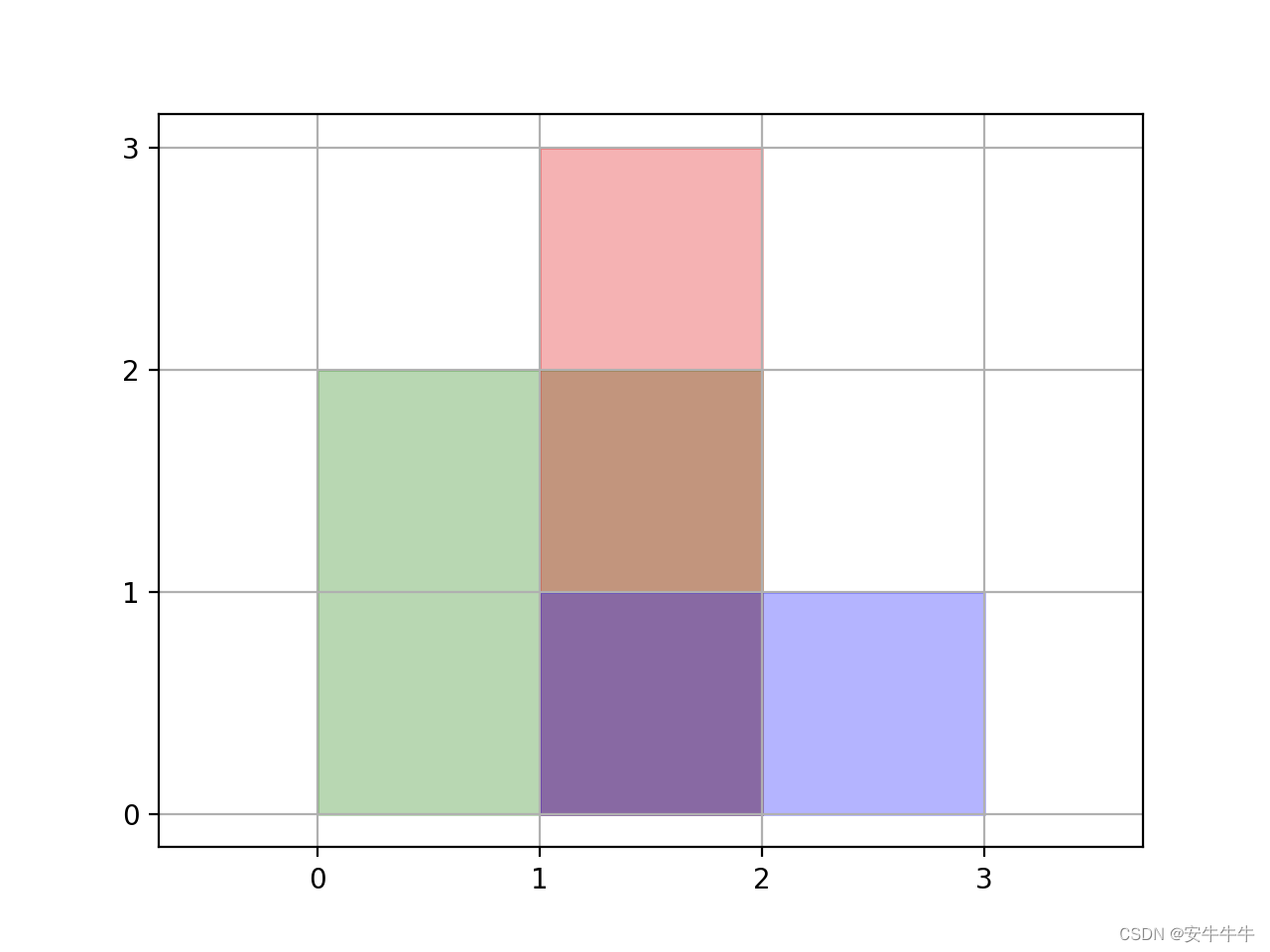
输入:rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出:6
解释:如图所示,三个矩形覆盖了总面积为6的区域。
从(1,1)到(2,2),绿色矩形和红色矩形重叠。
从(1,0)到(2,3),三个矩形都重叠。
示例 2:
输入:rectangles = [[0,0,1000000000,1000000000]]
输出:49
解释:答案是 10^18 对 (10^9 + 7) 取模的结果, 即 49 。
提示:
- 1 <= rectangles.length <= 200
- rectanges[i].length = 4
- 0 <= xi1, yi1, xi2, yi2 <= 109
- 矩形叠加覆盖后的总面积不会超越 263 - 1 ,这意味着可以用一个 64 位有符号整数来保存面积结果。
方案一:O(n2logn)的时间复杂度
- 获取所有矩形的两条竖边的 x 坐标,按 x 从小到大排序。
- 遍历 x 坐标,值相同的跳过(可以在第一步做一个去重), 找到两个不同的坐标 x1 , x2。
- 遍历所有的矩形,记录下横坐标区间覆盖了 x1, x2 的矩形的两个 y 坐标。
- 统计出这些 y 坐标的总长度(高度),乘以 x2 - x1 (宽度),就是(x1, x2) 区间中矩形的面积
- 继续遍历,遍历完所有的区间,就是所有矩形的总面积
例:
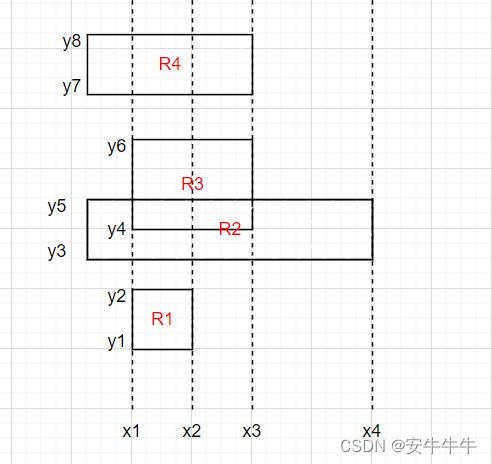
遍历到 (x1, x2) 区间时, 有 4 个矩形覆盖了这个区间:R1、R2、R3、R4;统计出来的高度为:H = (y2 - y1) + (y6 - y3) + (y8 - y7)。面积为: H * (x2 - x1)。(R2 和 R3 重复的面积没有算,统计出来的高度是 y6 - y3, 而不是 y6 - y4 + y5 - y3)
上一个遍历的区间是前一个 x 到 x1, 下一个要遍历的区间是 (x2, x3)。因为 x 坐标是根据矩形的竖边确定的,所以不会错过任何矩形的面积漏算,一定会统计出所有的面积。
int rectangleArea(vector<vector<int>>& rectangles) {
const int MOD = 1e9 + 7;
vector<int> vecX;
for (auto &rect : rectangles) {
vecX.push_back(rect[0]);
vecX.push_back(rect[2]);
}
sort(vecX.begin(), vecX.end());
long ans = 0;
for (int i = 1; i < vecX.size(); ++i) {
int a = vecX[i - 1], b = vecX[i];
if (a == b)
continue;
vector<vector<int>> lines;
for (auto &rect : rectangles) {
if (rect[0] <= a && b <= rect[2]) { // 矩形覆盖当前区间(矩形在区间内),将矩形的y坐标记录下来
lines.push_back({rect[1], rect[3]});
}
}
sort(lines.begin(), lines.end(), [](vector<int>& a, vector<int>& b) -> bool {
return a[0] < b[0] || (a[0] == b[0] && a[1] < b[1]);
});
long height = 0, prey1 = -1, prey2 = -1;
for (auto &cur : lines) {
if (cur[0] > prey2) { // 和上一个纵区间不相交
height += prey2 - prey1;
prey1 = cur[0];
prey2 = cur[1];
} else if (cur[1] > prey2) { // 和上一个纵区间相交,合并成一个
prey2 = cur[1];
}
}
height += prey2 - prey1;
ans += height * (b - a);
ans %= MOD;
}
return ans;
}
方案二:O(n2) 的时间复杂度
int rectangleArea(vector<vector<int>>& rectangles) {
int n = rectangles.size();
vector<int> hbound;
for (const auto& rect: rectangles) {
hbound.push_back(rect[1]);
hbound.push_back(rect[3]);
}
sort(hbound.begin(), hbound.end());
hbound.erase(unique(hbound.begin(), hbound.end()), hbound.end()); // 删除重复的 y 坐标
int m = hbound.size();
vector<int> seg(m - 1);
vector<tuple<int, int, int>> sweep; // 分别表示:x 坐标,第几个矩形,左边界还是右边界
for (int i = 0; i < n; ++i) {
sweep.emplace_back(rectangles[i][0], i, 1);
sweep.emplace_back(rectangles[i][2], i, -1);
}
sort(sweep.begin(), sweep.end());
long long ans = 0;
for (int i = 0; i < sweep.size(); ++i) {
int j = i;
while (j + 1 < sweep.size() && get<0>(sweep[i]) == get<0>(sweep[j + 1])) {
++j; // 找到横坐标相同的左右边界
}
if (j + 1 == sweep.size()) {
break;
}
// 一次性地处理掉一批横坐标相同的左右边界
for (int k = i; k <= j; ++k) {
auto&& [_, idx, diff] = sweep[k];
int y1 = rectangles[idx][1], y2 = rectangles[idx][3];
for (int x = 0; x < m - 1; ++x) {
if (y1 <= hbound[x] && hbound[x + 1] <= y2) { // 纵坐标包含了
seg[x] += diff;
}
}
}
int cover = 0;
for (int k = 0; k < m - 1; ++k) {
if (seg[k] > 0) {
cover += (hbound[k + 1] - hbound[k]);
}
}
ans += static_cast<long long>(cover) * (get<0>(sweep[j + 1]) - get<0>(sweep[j]));
i = j;
}
return ans % static_cast<int>(1e9 + 7);
}
方案三: O(nlogn)的时间复杂度
struct Segtree {
int cover;
int length;
int max_length;
};
int rectangleArea(vector<vector<int>>& rectangles) {
int n = rectangles.size();
for (const auto& rect: rectangles) {
hbound.push_back(rect[1]);
hbound.push_back(rect[3]);
}
sort(hbound.begin(), hbound.end());
hbound.erase(unique(hbound.begin(), hbound.end()), hbound.end());
int m = hbound.size();
// 线段树有 m-1 个叶子节点,对应着 m-1 个会被完整覆盖的线段,需要开辟 ~4m 大小的空间
tree.resize(m * 4 + 1);
init(1, 1, m - 1);
vector<tuple<int, int, int>> sweep;
for (int i = 0; i < n; ++i) {
sweep.emplace_back(rectangles[i][0], i, 1);
sweep.emplace_back(rectangles[i][2], i, -1);
}
sort(sweep.begin(), sweep.end());
long long ans = 0;
for (int i = 0; i < sweep.size(); ++i) {
int j = i;
while (j + 1 < sweep.size() && get<0>(sweep[i]) == get<0>(sweep[j + 1])) {
++j;
}
if (j + 1 == sweep.size()) {
break;
}
// 一次性地处理掉一批横坐标相同的左右边界
for (int k = i; k <= j; ++k) {
auto&& [_, idx, diff] = sweep[k];
// 使用二分查找得到完整覆盖的线段的编号范围
int left = lower_bound(hbound.begin(), hbound.end(), rectangles[idx][1]) - hbound.begin() + 1;
int right = lower_bound(hbound.begin(), hbound.end(), rectangles[idx][3]) - hbound.begin();
update(1, 1, m - 1, left, right, diff);
}
ans += static_cast<long long>(tree[1].length) * (get<0>(sweep[j + 1]) - get<0>(sweep[j]));
i = j;
}
return ans % static_cast<int>(1e9 + 7);
}
void init(int idx, int l, int r) {
tree[idx].cover = tree[idx].length = 0;
if (l == r) {
tree[idx].max_length = hbound[l] - hbound[l - 1];
return;
}
int mid = (l + r) / 2;
init(idx * 2, l, mid);
init(idx * 2 + 1, mid + 1, r);
tree[idx].max_length = tree[idx * 2].max_length + tree[idx * 2 + 1].max_length;
}
void update(int idx, int l, int r, int ul, int ur, int diff) {
if (l > ur || r < ul) {
return;
}
if (ul <= l && r <= ur) {
tree[idx].cover += diff;
pushup(idx, l, r);
return;
}
int mid = (l + r) / 2;
update(idx * 2, l, mid, ul, ur, diff);
update(idx * 2 + 1, mid + 1, r, ul, ur, diff);
pushup(idx, l, r);
}
void pushup(int idx, int l, int r) {
if (tree[idx].cover > 0) {
tree[idx].length = tree[idx].max_length;
}
else if (l == r) {
tree[idx].length = 0;
}
else {
tree[idx].length = tree[idx * 2].length + tree[idx * 2 + 1].length;
}
}
private:
vector<Segtree> tree;
vector<int> hbound;