- 模拟退火算法来源:
- 固体退火原理,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。
- 处在低温状态时,固体中分子具有的内能很低,在原本的位置上做小范围的振动。若是将固体加热到一定温度,分子内能将会增加,热运动加剧,分子排列的无序度增加。此时再将温度缓缓降低,在每个温度都达到平衡态(即准静态过程),分子具有的能量逐渐降低,最终回归到有序排列的状态,分子内能也跟着降到最低。
- 爬山算法主要缺点:会陷入局部最优解
- 比喻对比爬山算法和模拟退火算法:
- 爬山算法:兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法,它不能保证局部最优值就是全局最优值。
- 模拟退火:兔子喝醉了。它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高方向跳去。这就是模拟退火。
- 模拟退火算法从某一较高初温出发,伴随温度参数的不断下降,结合一定的概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。对于下一个解的接受概率:
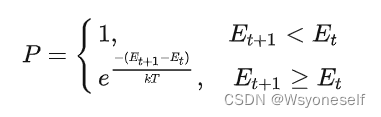 假设当前时刻搜索的解为xt,对应的系统能量(目标函数)为Et,对搜索点施加随机扰动,产生新解xt+1,相应地,系统能量为Et+1,那么系统对搜索点从xt到xt+1转变的接受概率就为上公式。
假设当前时刻搜索的解为xt,对应的系统能量(目标函数)为Et,对搜索点施加随机扰动,产生新解xt+1,相应地,系统能量为Et+1,那么系统对搜索点从xt到xt+1转变的接受概率就为上公式。 - 将温度T当作控制参数,目标函数值f视为内能E,而固体在某温度T时的一个状态对应一个解,然后算法试图随着控制参数T的降低,使目标函数f(内能E)也逐渐降低,直至趋于全局最小值(退火中低温时的最低能量状态),就像金属退火过程一样。
- 模拟退火的流程
- 算法实质分两层循环,在任一温度水平下,随机扰动产生新解,并计算目标函数值的变化,决定是否被接受。由于算法初始温度比较高,这样,使E增大的新解在初始时也可能被接受,因而能跳出局部极小值,然后通过缓慢地降低温度,算法就最终可能收敛到全局最优解,具体流程为如下
- 令T=T0,表示开始退火的初始温度,随机产生一个初始解x0,并计算对应的目标函数值E(x0);
- 令T=kT,其中k取值0到1之间,为温度下降速率;
- 对当前解x_t施加随机扰动,在其邻域内产生一个新解x_(t+1),并计算对应的目标函数值E(x_(t+1)),计算△E=E(x_(t+1))-E(x_t)
- 若△E<0,接受新解作为当前解,否则按照概率e^(△E/(kT))判断是否接受新解;
- 在温度T下,重复L次扰动和接受过程,即执行步骤3和4;
- 判断温度是否达到终止温度水平,若是则终止算法,否则返回步骤2
- 需要注意的点:
- 初始点的选取对算法结果有一定的影响,最好是多次运行对结果进行综合判断。
- 在算法运行初期,温度下降快,避免接受过多的差结果。当运行时间增加,温度下降减缓,以便于更快稳定结果。
- 当迭代次数增加到一定次数时,结果可能已经达到稳定,但是距离算法结束还有一段时间。在设计程序时应该加入适当的输出条件,满足输出条件即可结束程序。
- 模拟退火算法是通过赋予搜索过程一种时变且最终趋于零的概率突跳性,从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。算法从某一较高初温出发,伴随温度参数的不断下降,结合一定的概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优
模拟退火--学习笔记
news2026/2/10 8:20:04
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/25626.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
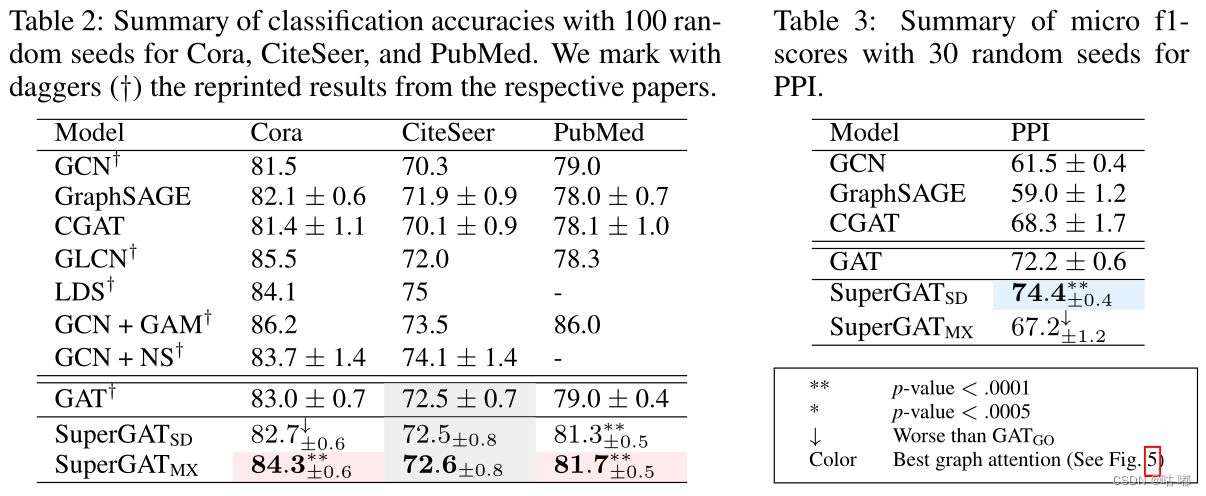
【图神经网络论文整理】(三)—— HOW TO FIND YOUR FRIENDLY NEIGHBORHOOD:SuperGAT
ICLR 2021Dongkwan Kim & Alice Oh论文地址
本文介绍的论文是《HOW TO FIND YOUR FRIENDLY NEIGHBORHOOD: GRAPH ATTENTION DESIGN WITH SELF-SUPERVISION》。
该篇论文提出了一个新的网络模型SuperGAT,目的是解决当图中存在噪声能够学习到更多的表达注意力&a…
实体店做微信商城小程序制作步骤_分享微信商城小程序的作用
各行各业都在用微商城小程序开店,不管是餐饮店还是便利店,还是五金店。都是可以利用微信小程序开一个线上店铺。实现线上跟线下店铺更加全面的结合。维护好自己的老客户。让您的客户给您拉新,带来新客户。 小程序经过这几年的快速发展和不断升…
计算机毕业设计之java+ssm企业销售管理系统
项目介绍
本企业销售管理系统主要包括系统用户管理模块、商品信息模块、进货入库管理、员工信息管理、销售管理、登录模块、和退出模块等多个模块系统采用了jsp的mvc框架,SSM(springMvcspringMybatis)框架进行开发,本系统是独立的运行,不依附于其他系统,…
Day4:写前端项目(html+css+js)
xiao效果: 页面布局
使用grid
<div class"grid-container"><div><h1 class"uppercase ff-sans-cond letter-spacing-2 text-accent"> so, you want to travel to<span class"uppercase letter-spacing-2 fs-900 te…
【无线传感器】使用 Mamdani 模糊推理系统改进无线传感器网络路由和数据包传递(Matlab代码实现)
👨🎓个人主页:研学社的博客 💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜…
操作系统的奋斗(二)进程与线程
第二章 进程与线程2.1进程与线程2.1.1进程的概念、特征、状态与转换2.1.2进程的组织、控制、通信2.1.3进程和多线程模型2.2处理机调度2.2.1调度的概念、目标、实现2.2.2典型的调度算法2.2.3进程切换2.3同步与互斥2.3.1同步与互斥的基本概念2.3.2实现临界区互斥的基本办法2.3.3互…
泊松随机变量的分解与求和
1.泊松随机变量的分解
假设传感器发出的信号为0-1信号.发出1的概率为,发出0的概率为 ,并且和以前所发的信号独立.现在假设一定时间内发出信号的个数为泊松随机变量,其参数为, 可以证明在同一段时间内发出1的个数也是泊松随机变量,其参数为.
证明&#…
PTA题目 A除以B
真的是简单题哈 —— 给定两个绝对值不超过100的整数A和B,要求你按照“A/B商”的格式输出结果。
输入格式:
输入在第一行给出两个整数A和B(−100≤A,B≤100),数字间以空格分隔。
输出格式:
在一行中输出…
Data-Efficient Backdoor 论文笔记
#论文笔记#
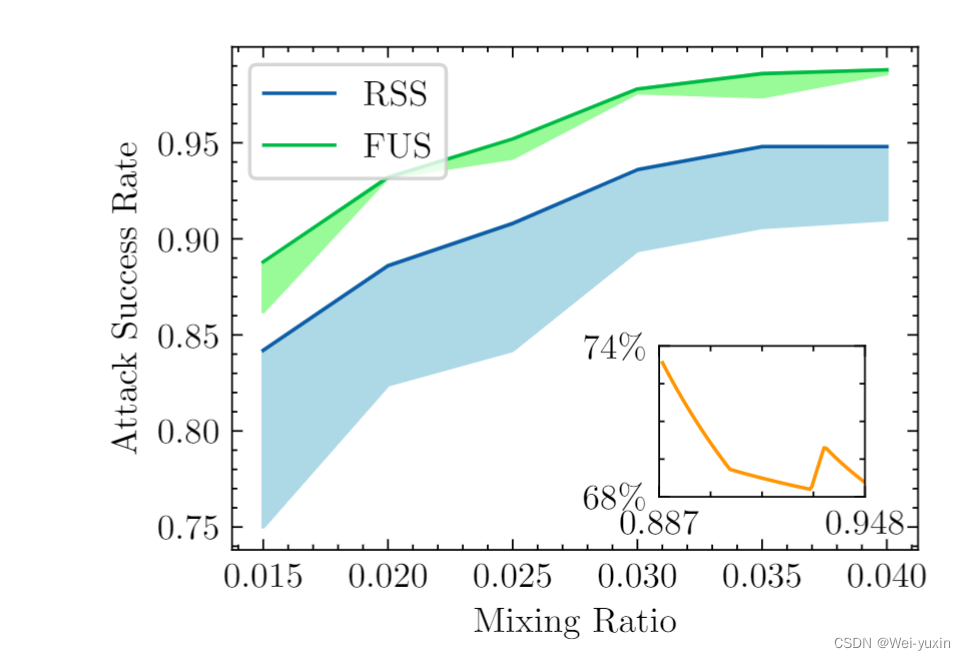
1. 论文信息
论文名称Data-Efficient Backdoor作者Pengfei Xia 中国科学技术大学会议/出版社IJCAI 2022pdf📄在线pdf代码💻pytorch概要:本文是 backdoor attack 中的数据加毒。不同于以往随机在干净数据中选择样本加毒的方法&am…
磁盘怎么删除分区,磁盘管理怎么删除分区
为了高效地利用磁盘分区,会删除部分磁盘分区,但是很多的用户都不知道应该怎么删除磁盘分区,所以,易我小编将讲解磁盘怎么删除分区。 一、为什么要删除磁盘分区
因为不同用户的磁盘分区管理需求不同,为了适应用户的具体…
spring boot yaml自定义配置传入代码
目录 一、在项目代码中,直接读取配置文件application.yml中的数据
二、通过yaml配置文件,给类注入数据 一、在项目代码中,直接读取配置文件application.yml中的数据
使用Value注解。
如:
在spring boot 中,applica…
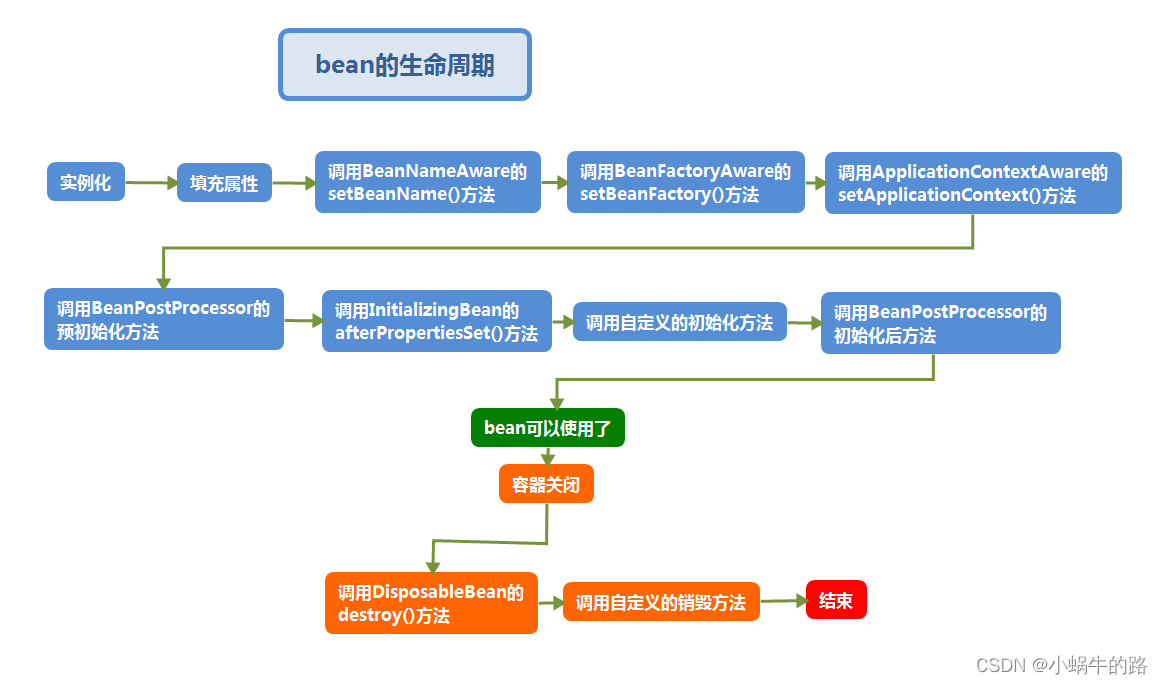
Spring实战之容器、上下文、Bean的生命周期
一、Spring容器
在基于Spring的应用中,你的应用对象生存于Spring容器(container)中,Spring容器负责创建对象,装配它们,配置它们并管理它们的整个生命周期,从生存到死亡。(在这里&am…
程序运行只是单单的编译吗?一文让你深入理解程序运行的过程
前言: 写了这么长时间的c语言代码,我们都没有想过为什么要写头文件吗,而程序执行的过程又是如何呢?只有编译吗 ?要知道机器只能读懂二进制但我们所写的代码编译器是如何读懂的呢?这一篇文章看后一定能解决以…
数据结构之Trie树
Trie树:
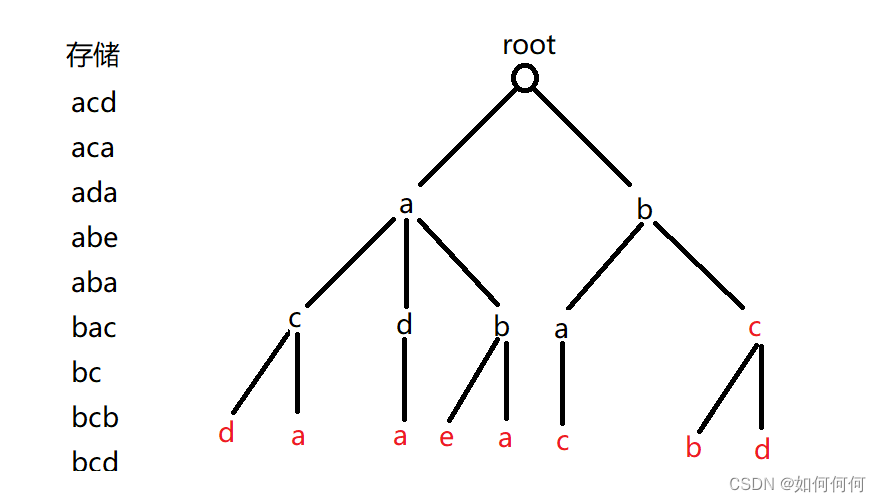
Tire树可以较为高效的存储和查找字符串集合。
存储方式: 首先Trie有一个根节点,我们按从前往后的顺序将字符串的每个位置上的字符存储到树的每一层中,这样我们存储多个字符串时就可以消除一部分冗余,在查询字…
期货开户后需要银期转账绑定
一、期货公司正规性
如何判断期货公司是否正规?
1、 中国证监会官网有公布所有正规期货公司(一共150家)名录的,我们可以直接参考证监会发布链接:期货公司名录
2、如果你懒得从名录中一个个找,也可以直接…
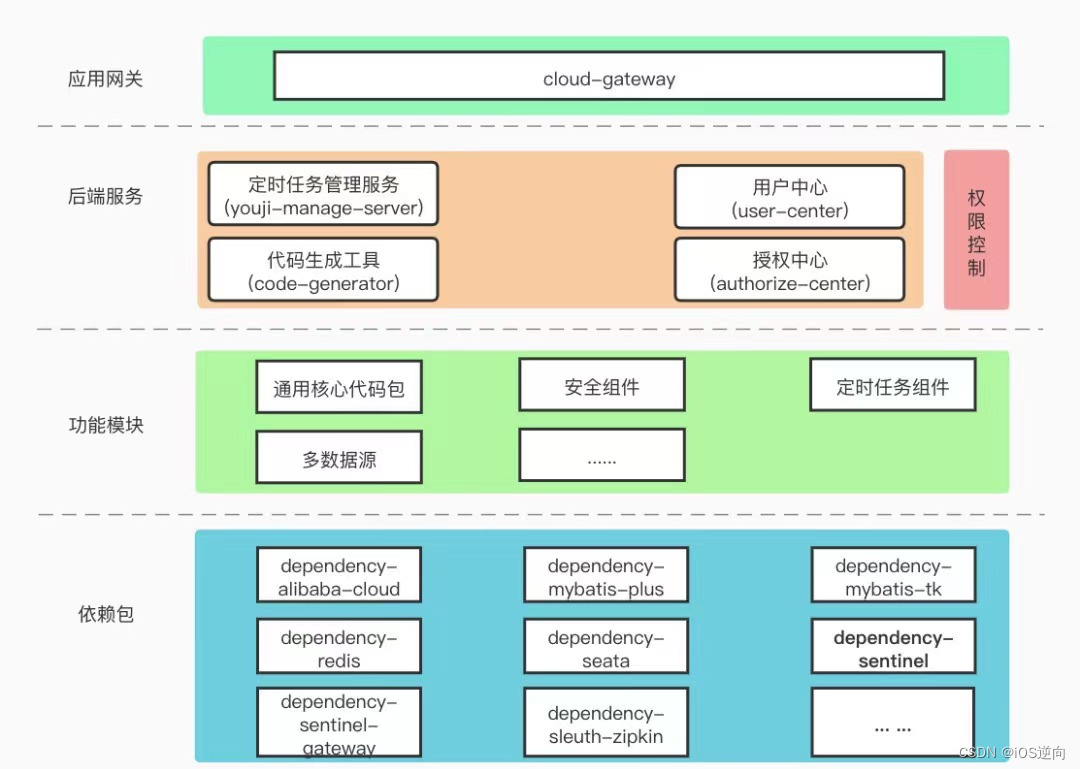
一款不错的SpringCloud 脚手架项目
文章目录 I 一款不错的SpringCloud 脚手架项目1.1 项目概述1.2 本地启动II. Swagger RESTful 风格的 Web 服务框架2.1 组成部分2.2 springfoxIII 相关辅助脚本3.1 pod 辅助脚本3.2 git 辅助脚本I 一款不错的SpringCloud 脚手架项目 1.1 项目概述 springboot+springcloud注册中心…
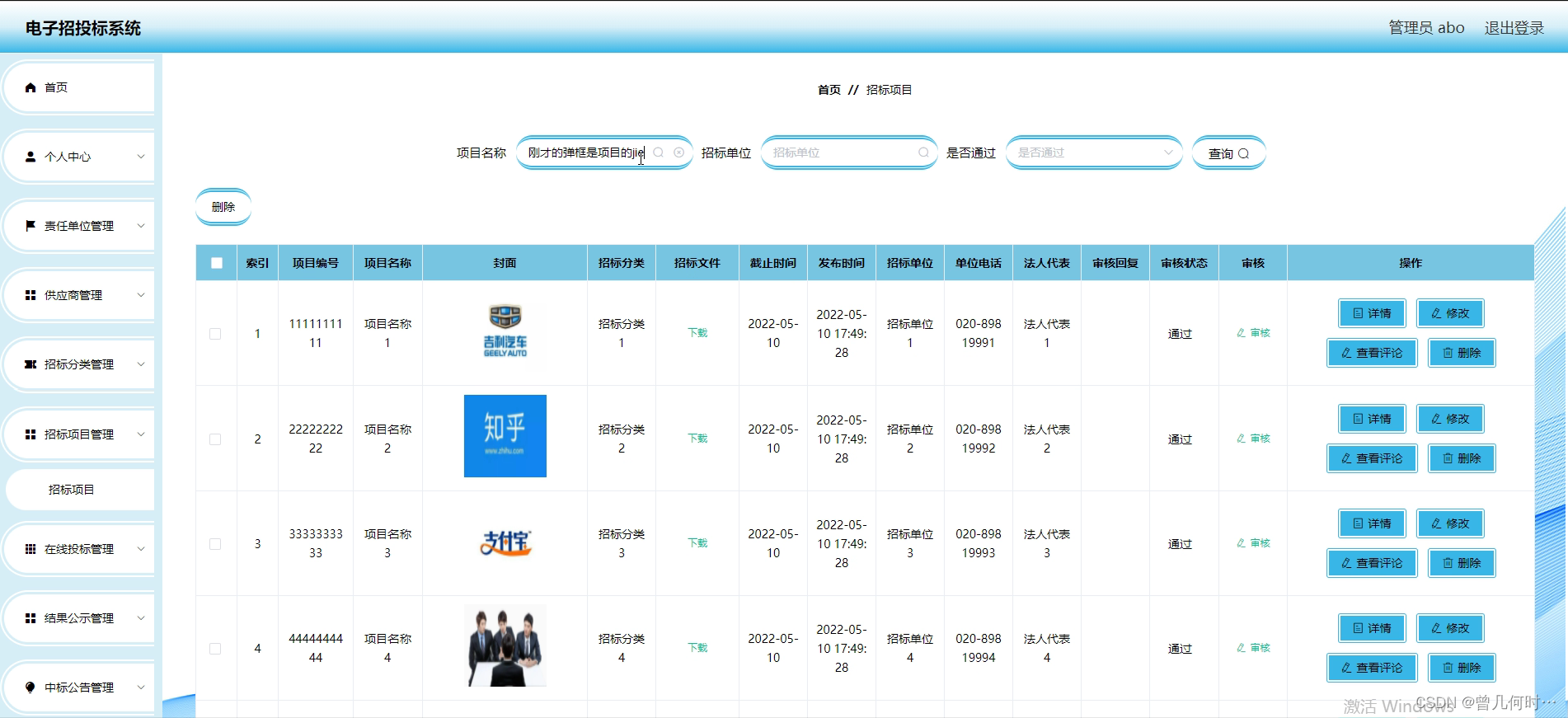
基于SpringBoot的电子招标投标管理系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SpringBoot 前端:HTML、Vue 数据库:MySQL5.7 数据库管理工具:Navicat 12 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否…
Android BottomSheetDialogFragment 使用详解,设置圆角、固定高度、默认全屏等
转载请标明出处:http://blog.csdn.net/zhaoyanjun6/article/details/127967304 本文出自【赵彦军的博客】 文章目录效果BottomSheetBottomSheetDialogBottomSheetDialogFragment圆角效果去掉背景蒙版设置蒙版透明度点击 dialog 外部区域,dialog 不消失禁…
STC51单片机37——定时器流水灯
// 12MHz晶振 #include "reg52.h" #include "intrins.h" #define time (65536-50000) // 单次定时50ms unsigned char cn; unsigned char temp; unsigned char dir;
void main(void) { cn20; //20*50ms1s temp0x80; dir0; TMOD 0x…
Vue简单示例——weex
weex的生命周期:
因为我们的Weex和Vue是绑定在一起的,所以我们讨论关于生命周期时,说的实际上是在Weex中可以使用的Vuex的生命周期,也就是Weex对于Vue生命周期的支持,好消息,Weex支持大部分的Vue中的生命周…