泊松随机变量的分解与求和

news2024/12/27 9:14:37

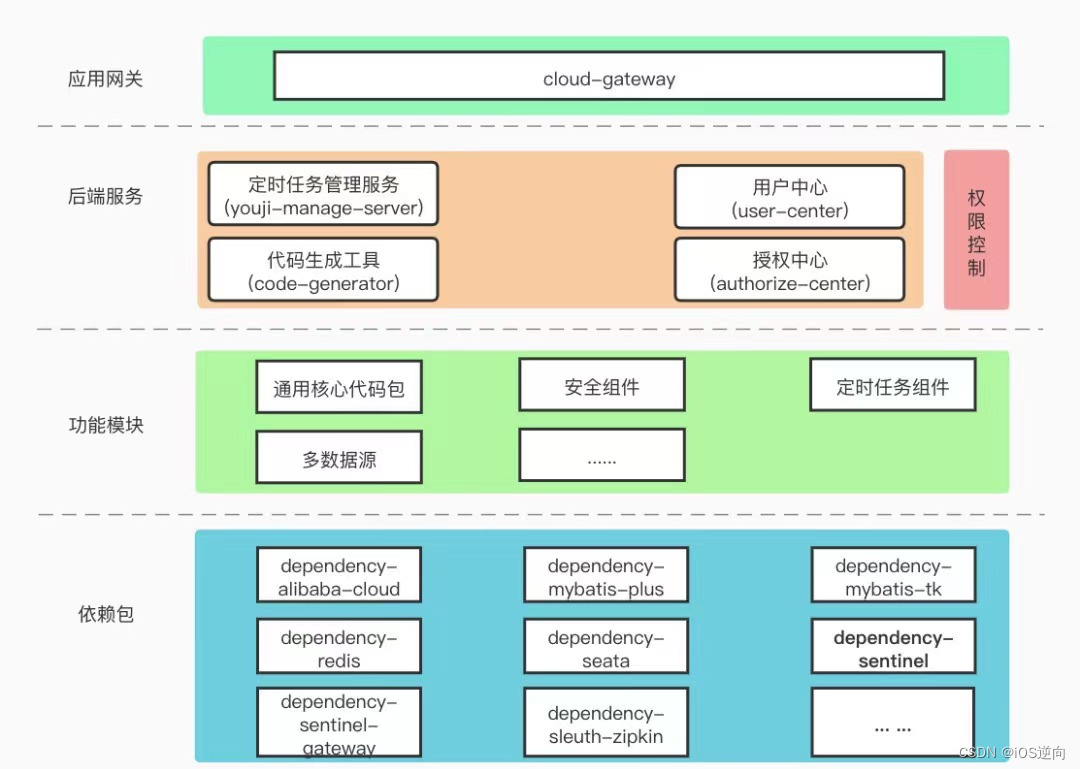
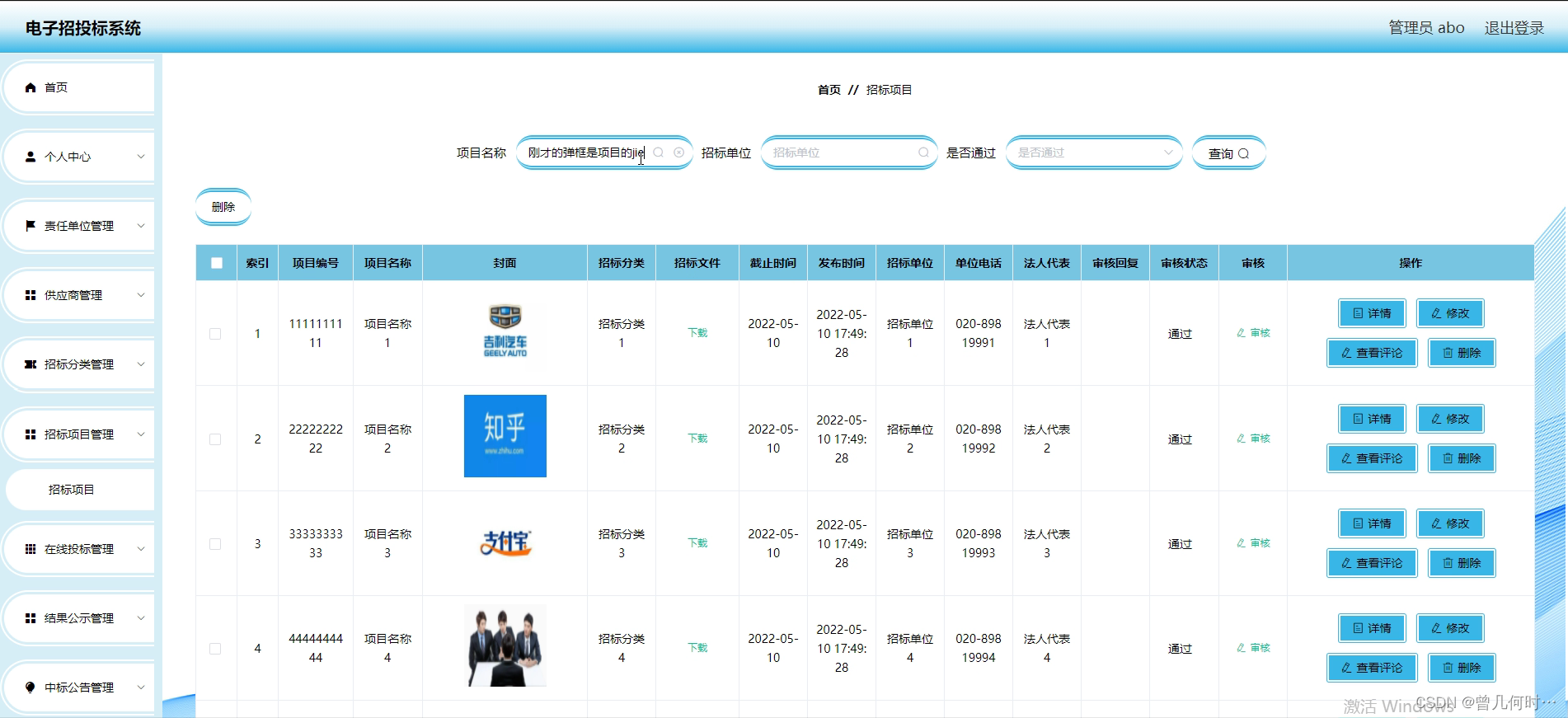
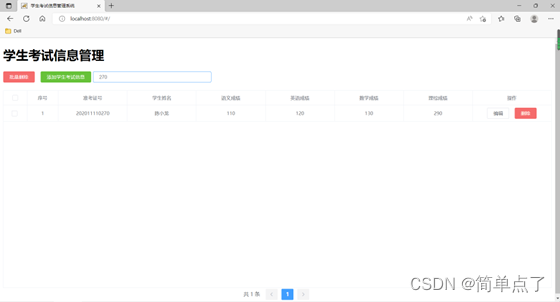
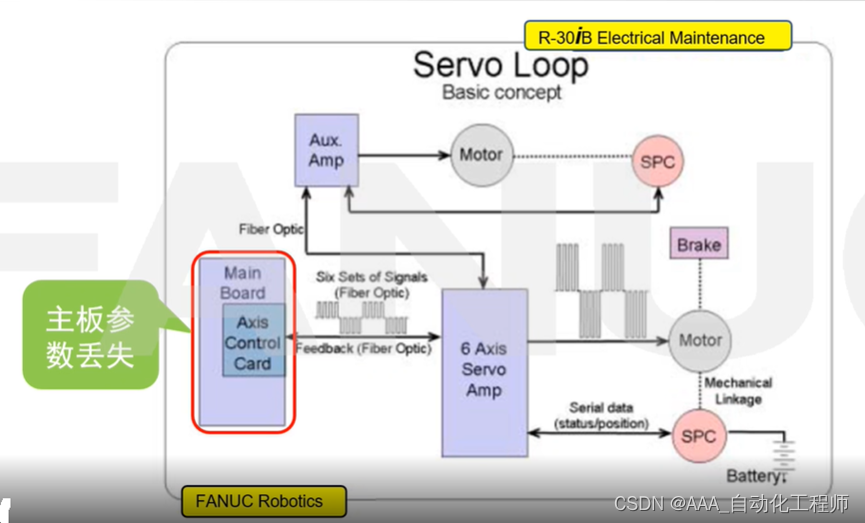
1.泊松随机变量的分解

假设传感器发出的信号为0-1信号.发出1的概率为p,发出0的概率为 1-p,并且和以前所发的信号独立.现在假设一定时间内发出信号的个数为泊松随机变量，其参数为\lambda, 可以证明在同一段时间内发出1的个数也是泊松随机变量，其参数为p\lambda.

证明：设X 和Y分别为同一时间段内发出的信号1和0的个数，那么Z=X+Y就是这一时间段内发出信号的个数，利用全概率公式，得到

        \begin{align} P(X=n,Y=m) &=P(X=n,Y=m|Z=n+m)P(Z=n+m) \nonumber \\ &=\binom{n+m}{n}p^n(1-p)^m\cdot \frac{e^{-\lambda}\lambda^{n+m}}{(n+m)!} \nonumber \\ &=\frac{e^{-\lambda p}(\lambda p)^n}{n!}\cdot \frac{e^{-\lambda(1-p)}\(\lambda(1-p))^{m}}{m!} \nonumber \end{align}

由此得到

                \begin{align} P(X=n) &=\sum_{m=0}^{\infty}P(X=n,Y=m) \nonumber \\ &=\frac{e^{ -\lambda p}(\lambda p)^n}{n!}e^{ -\lambda (1-p)}\sum_{m=0}^{\infty}\frac{((\lambda (1-p))^m}{m!} \nonumber \\ & =\frac{e^{ -\lambda p}(\lambda p)^n}{n!}e^{ -\lambda (1-p)}e^{ \lambda (1-p)} \nonumber \\ & = \frac{e^{ -\lambda p}(\lambda p)^n}{n!} \nonumber \end{align}

这说明X 是一个泊松随机变量，参数为\lambda p.

2.个数服从泊松分布的随机变量之和

用矩母函数证明个数服从泊松分布的多个独立同分布的伯努利随机变量之和服从泊松分布

证明：假设N是服从参数为\lambda的泊松分布的随机变量. X_i(i=1,2,...,N)是独立的参数为p的随机变量，可令

                ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​L =X_1+X_2+...+X_N

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/25614.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

PTA题目 A除以B

PTA题目 A除以B

真的是简单题哈 —— 给定两个绝对值不超过100的整数A和B，要求你按照“A/B商”的格式输出结果。 输入格式： 输入在第一行给出两个整数A和B（−100≤A,B≤100），数字间以空格分隔。 输出格式： 在一行中输出…
阅读更多...
Data-Efficient Backdoor 论文笔记

Data-Efficient Backdoor 论文笔记

#论文笔记# 1. 论文信息 论文名称Data-Efficient Backdoor作者Pengfei Xia 中国科学技术大学会议/出版社IJCAI 2022pdf📄在线pdf代码💻pytorch概要：本文是 backdoor attack 中的数据加毒。不同于以往随机在干净数据中选择样本加毒的方法&am…
阅读更多...
磁盘怎么删除分区，磁盘管理怎么删除分区

磁盘怎么删除分区，磁盘管理怎么删除分区

为了高效地利用磁盘分区，会删除部分磁盘分区，但是很多的用户都不知道应该怎么删除磁盘分区，所以，易我小编将讲解磁盘怎么删除分区。 一、为什么要删除磁盘分区 因为不同用户的磁盘分区管理需求不同，为了适应用户的具体…
阅读更多...
spring boot yaml自定义配置传入代码

spring boot yaml自定义配置传入代码

目录 一、在项目代码中，直接读取配置文件application.yml中的数据 二、通过yaml配置文件，给类注入数据 一、在项目代码中，直接读取配置文件application.yml中的数据 使用Value注解。 如： 在spring boot 中，applica…
阅读更多...
Spring实战之容器、上下文、Bean的生命周期

Spring实战之容器、上下文、Bean的生命周期

一、Spring容器 在基于Spring的应用中，你的应用对象生存于Spring容器（container）中，Spring容器负责创建对象，装配它们，配置它们并管理它们的整个生命周期，从生存到死亡。（在这里&am…
阅读更多...
程序运行只是单单的编译吗？一文让你深入理解程序运行的过程

程序运行只是单单的编译吗？一文让你深入理解程序运行的过程

前言： 写了这么长时间的c语言代码，我们都没有想过为什么要写头文件吗，而程序执行的过程又是如何呢？只有编译吗 ？要知道机器只能读懂二进制但我们所写的代码编译器是如何读懂的呢？这一篇文章看后一定能解决以…
阅读更多...
数据结构之Trie树

数据结构之Trie树

Trie树： Tire树可以较为高效的存储和查找字符串集合。 存储方式： 首先Trie有一个根节点，我们按从前往后的顺序将字符串的每个位置上的字符存储到树的每一层中，这样我们存储多个字符串时就可以消除一部分冗余，在查询字…
阅读更多...
期货开户后需要银期转账绑定

期货开户后需要银期转账绑定

一、期货公司正规性 如何判断期货公司是否正规？ 1、 中国证监会官网有公布所有正规期货公司（一共150家）名录的，我们可以直接参考证监会发布链接：期货公司名录 2、如果你懒得从名录中一个个找，也可以直接…
阅读更多...
一款不错的SpringCloud 脚手架项目

一款不错的SpringCloud 脚手架项目

文章目录 I 一款不错的SpringCloud 脚手架项目1.1 项目概述1.2 本地启动II. Swagger RESTful 风格的 Web 服务框架2.1 组成部分2.2 springfoxIII 相关辅助脚本3.1 pod 辅助脚本3.2 git 辅助脚本I 一款不错的SpringCloud 脚手架项目 1.1 项目概述 springboot+springcloud注册中心…
阅读更多...
基于SpringBoot的电子招标投标管理系统

基于SpringBoot的电子招标投标管理系统

末尾获取源码 开发语言：Java Java开发工具：JDK1.8 后端框架：SpringBoot 前端：HTML、Vue 数据库：MySQL5.7 数据库管理工具：Navicat 12 服务器：Tomcat8.5 开发软件：IDEA / Eclipse 是否…
阅读更多...
Android BottomSheetDialogFragment 使用详解，设置圆角、固定高度、默认全屏等

Android BottomSheetDialogFragment 使用详解，设置圆角、固定高度、默认全屏等

转载请标明出处：http://blog.csdn.net/zhaoyanjun6/article/details/127967304 本文出自【赵彦军的博客】 文章目录效果BottomSheetBottomSheetDialogBottomSheetDialogFragment圆角效果去掉背景蒙版设置蒙版透明度点击 dialog 外部区域，dialog 不消失禁…
阅读更多...
STC51单片机37——定时器流水灯

STC51单片机37——定时器流水灯

// 12MHz晶振 #include "reg52.h" #include "intrins.h" #define time (65536-50000) // 单次定时50ms unsigned char cn; unsigned char temp; unsigned char dir; void main(void) { cn20; //20*50ms1s temp0x80; dir0; TMOD 0x…
阅读更多...
Vue简单示例——weex

Vue简单示例——weex

weex的生命周期： 因为我们的Weex和Vue是绑定在一起的，所以我们讨论关于生命周期时，说的实际上是在Weex中可以使用的Vuex的生命周期，也就是Weex对于Vue生命周期的支持，好消息，Weex支持大部分的Vue中的生命周…
阅读更多...
基于Vue+ElementUI+MySQL+Express的学生管理系统(3)

基于Vue+ElementUI+MySQL+Express的学生管理系统(3)

3.搭建学生考试信息的前端页面 1.在E:\vue\shiyan9目录下用cmd打开命令窗口。输入命令vue init webpack score-manage，创建一个基于webpack模板的项目。 图15 创建一个新的vue的脚手架的项目 2.执行cd score-manage，进入目录包下。下载依赖包。命令如下…
阅读更多...
Pytorch 图像增强 实现翻转裁剪色调等 附代码（全）

Pytorch 图像增强 实现翻转裁剪色调等 附代码（全）

目录前言1. 裁剪1.1 中心裁剪1.2 随机裁剪1.3 随机尺寸裁剪2. 翻转2.1 水平翻转2.2 垂直翻转2.3 随机旋转3. 色调3.1 灰度变换3.2 色彩抖动3.3 随机翻转颜色3.4 随机调整锐度3.5 高斯模糊4. 边缘填充5. 仿射变换前言 下文中有使用到plt，不懂的可看我这篇文章&#…
阅读更多...
doker中的Jenkins容器配置github

doker中的Jenkins容器配置github

1、在Jenkins插件 管理中下载github plugin和ssh和git插件 2、在Jenkins->系统管理->系统配置->github下配置凭据认证，添加凭证页面类型选择secret text 3、添加凭证页面secret栏输入githu token，其他任意输入 4、github token获取&#xf…
阅读更多...
FANUC机器人零点复归的报警原因分析和零点标定相关步骤

FANUC机器人零点复归的报警原因分析和零点标定相关步骤

FANUC机器人零点复归的报警原因分析和零点标定相关步骤 FANUC机器人零点复归时需要将机器人的机械信息与位置信息同步，来定义机器人的物理位置。 机器人通过闭环伺服系统来控制机器人各运动轴，当用户通过示教器点动机器人时，经过主板分析此命令后，带动电机旋转，电机上的SP…
阅读更多...
软件测试入门概念

软件测试入门概念

满足用户期望或正式规定文档（合同、标准、规范）所具有的条件和权能，包含用户需求和软件需求。 用户需求： 五花八门的用户需求，该需求比较简略。 软件需求： 又叫功能需求，该需求会详细描述开发…
阅读更多...
SLAM本质剖析-Boost之Geometry函数大全(二)

SLAM本质剖析-Boost之Geometry函数大全(二)

4. 点云处理 4.1 add_point 将一个点添加到另一个点 4.2 add_value 将相同的值添加到点的每个坐标 4.3 assign_point 用另一个点指定一个点 4.4 assign_value 为点的每个坐标指定相同的值 4.5 cross_product 计算两个向量的叉积 4.7 divide_point 将一点除以另一点…
阅读更多...
Python用27行代码绘制一幅满天星

Python用27行代码绘制一幅满天星

前言 大家早好、午好、晚好吖 ❤ ~ 每一个孩子都像星空中的一颗星星，散发着自己所特有的光芒照亮着整个夜空。 今天就带大家用27行Python代码绘制一幅满天星吧。 全局设置 在绘制满天星的过程中要运用到turtle工具，它是Python的标准库，也可…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023