如论文标题所示,CKKS允许复数和实数运算,是一个近似精度计算的方案,也就是解密出来的明文和加密之前的明文不会完全一致。也就是采用丢失部分精度来换取较高的效率。
CKKS的核心是把加密噪声视为近似计算误差的一部分,也就是解密出来的结果直接视为原始消息的近似值。将重要的消息放在MSB以防计算后数据被破坏,把误差放在LSB来保障安全性,如果误差噪声相比消息来说足够小,那么噪声就不会破坏消息,在加密之前,将消息乘以一个缩放因子扩大消息,这样就可以减少添加噪声带来的误差。由此,消息+噪声可以用来替代原消息。当然,CKKS还使用了重缩放技术来减小密文计算时的扩张问题(有点像BV11、BGV、BFV结合的思想)让密文规模呈线性增长而不是指数级以增大乘法次数,还能顺带消除LSB位上的噪声,有点类似舍入运算。
近似计算
当前的近似计算主要分为两类定点运算和浮点运算,区别在于缩放因子是否固定。

CKKS方案采用的是定点运算,更加稳定(浮点运算很复杂,很难确定位的变化)。
大致流程
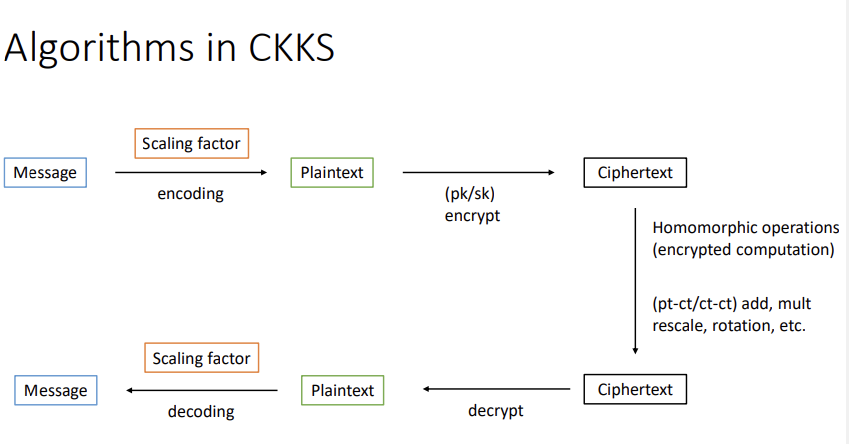
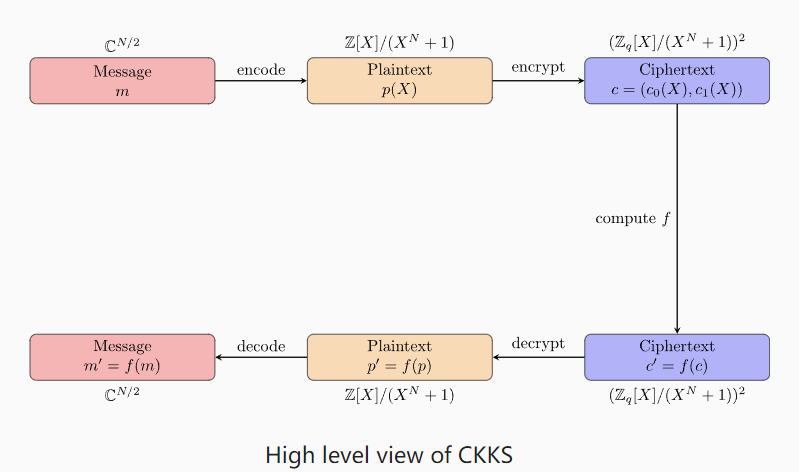
来看看整个算法的大致流程
大致包含编码(解码)、加解密、同态加乘、重缩放、自同构旋转等等。
这里的
C
N
/
2
\mathbb C^{N/2}
CN/2表示复数向量空间,
R
=
Z
[
X
]
/
(
X
N
+
1
)
R=\mathbb Z[X]/(X^N+1)
R=Z[X]/(XN+1),
R
q
=
Z
[
X
]
q
/
(
X
N
+
1
)
R_q =\mathbb Z[X]_q/(X^N+1)
Rq=Z[X]q/(XN+1)
编码与解码
一般的基于RLWE同态算法如BGV、BFV等的明文空间都是整数多项式,而CKKS由于是进行复数(实数)计算,它的消息空间是复数空间,为此,需要将消息从复数向量给“编码”成整数多项式。也就是实现
C
N
/
2
→
R
=
Z
[
X
]
/
(
X
N
+
1
)
\mathbb C^{N/2} \rightarrow R=\mathbb Z[X]/(X^N+1)
CN/2→R=Z[X]/(XN+1)映射。

一些概念
- 分圆多项式 Φ M ( X ) = X N + 1 \Phi_M(X) = X^N+1 ΦM(X)=XN+1,度数 N = ϕ ( M ) N=\phi(M) N=ϕ(M)(就是欧拉函数),它有 N N N个本原根,记为 ξ i , i ∈ Z M ∗ \xi^i,i \in \mathbb Z^*_M ξi,i∈ZM∗(i属于模M的剩余类,个数为欧拉函数个,如M=8,N就等于4,i就为1,3,5,7)
- 把一个多项式解码为一个向量,假定多项式为 m ( X ) m(X) m(X),消息空间的向量为 z z z,有 m ( ξ i ) = z i m(\xi^i)=z_i m(ξi)=zi,把这个转换定义为 σ ( m ) = ( m ( ξ ) , m ( ξ 3 ) , … , m ( ξ 2 N − 1 ) ) \sigma(m)=(m(\xi),m(\xi^3),\dots,m(\xi^{2N-1})) σ(m)=(m(ξ),m(ξ3),…,m(ξ2N−1))(原文中也叫正则嵌入),也就是把多项式根代入,就能得到对应的唯一的向量值。
消息为复数向量,要将它编码为多项式,需要进行上面的逆操作 σ − 1 \sigma^{-1} σ−1,得到如下结论 ∑ j = 0 N − 1 α j ( ξ 2 i − 1 ) j = z i , i = 1 , … , N \sum_{j=0}^{N-1} \alpha_{j}\left(\xi^{2 i-1}\right)^{j}=z_{i}, i=1, \ldots, N ∑j=0N−1αj(ξ2i−1)j=zi,i=1,…,N,可以简化为 A α = z A\alpha=z Aα=z(其中 A A A是一个范德蒙矩阵, α \alpha α是多项式的系数)
- H = { z ∈ C N : z j = z N − j ‾ } \mathbb H = \{z\in \mathbb C^N:z_j=\overline{z_{N-j}}\} H={z∈CN:zj=zN−j}( R [ x ] R[x] R[x]实数)
- σ ( R ) ⊂ H \sigma(R) \subset \mathbb H σ(R)⊂H( Z [ x ] Z[x] Z[x]整数)
- π : ∀ t ∈ H , π ( t ) = ( t 0 , t 1 , … , t N / 2 ) ∈ C N / 2 \pi: \forall t \in \mathbb H,\pi(t)=(t_0,t_1,\dots,t_{N/2}) \in \mathbb C^{N/2} π:∀t∈H,π(t)=(t0,t1,…,tN/2)∈CN/2:逆操作就是将向量取共轭,然后拼接到原向量的尾部,以达到扩张的目的。
- 编码的简单描述就是 m ( ξ i ) = Δ ⋅ z i m(\xi^i)=\Delta\cdot z_i m(ξi)=Δ⋅zi
步骤
编码具体步骤如下
-
取 z ∈ C N / 2 z \in \mathbb C^{N/2} z∈CN/2:
-
将扩张维度到 N N N: π − 1 ( z ) ∈ H \pi^{-1}(z) \in \mathbb H π−1(z)∈H:
从消息空间取出的消息是 N / 2 N/2 N/2维的复向量,需要将它扩充到 N N N维,方法就是对它取一下共轭(复数的操作,就是实部不变,虚部取反),再将它和原向量拼接到一起得到一个增广的 N N N维消息。
- 为保持精确度所乘以一个缩放因子 Δ \Delta Δ:
后面的操作出来需要用到取整,即将实数多项式变为整数多项式,如果直接取整那么误差会很大,所以这里乘以了一个缩放因子,之后再进行取整,这样可以尽可能的保留小数位上的数,提高精确度。
- 取整到 σ ( R ) \sigma(R) σ(R): ⌊ Δ ⋅ π − 1 ( z ) ⌉ σ ( R ) ∈ σ ( R ) \left\lfloor\Delta \cdot \pi^{-1}(z)\right\rceil_{\sigma(\mathcal{R})} \in \sigma(R) ⌊Δ⋅π−1(z)⌉σ(R)∈σ(R):
由于任给一个复向量 z ∈ C N / 2 z\in \mathbb C^{N/2} z∈CN/2,它的 π − 1 ( z ) \pi^{-1}(z) π−1(z)是不一定落在 σ ( R ) \sigma(R) σ(R)上的,所以需要一个取整操作,使其落在范围内。(其实就是把实数变为整数)
- 使用 σ \sigma σ进行编码: m ( X ) = σ − 1 ( ⌊ Δ ⋅ π − 1 ( z ) ⌉ σ ( R ) ) ∈ R m(X)=\sigma^{-1}(\lfloor\Delta \cdot\pi^{-1}(z) \rceil_{\sigma(\mathbb{R})}) \in R m(X)=σ−1(⌊Δ⋅π−1(z)⌉σ(R))∈R:
这一步就是转变为多项式。
图解如下

解码就是编码逆操作。
大致就是这个过程,可能有不少数学错误(非数学系,能写到这个程度已经很尽力了),总之大概能够理解就行了。
编码解码的算法如下:

对于理解后面方案来说,知道算法名字和参数就行了。
方案
大致包含密钥生成,编码与解码,加解密,和重缩放(也叫模交换)
先提一嘴模数的选取:选取一个模数
q
0
>
0
q_0>0
q0>0和一个特殊的基模数
p
>
0
p>0
p>0(更精确的说是接近
Δ
\Delta
Δ),用它们组成一个模数链
q
l
=
q
0
⋅
p
l
=
q
0
⋅
p
1
p
2
…
p
l
,
0
<
l
≤
L
q_l=q_0 \cdot p^l= q_0 \cdot p_1p_2\dots pl,0<l\le L
ql=q0⋅pl=q0⋅p1p2…pl,0<l≤L,就像BGV里面的模交换一样,这个将用于重缩放。
至于为什么要拆成两个相乘而不是用一个数,原因在于,CKKS需要100位,而目前计算机只有64位,于是采用了中国剩余定理将大数分成小数分别来存。
CKKS用了多种分布(对于理解方案来说不是重点),具体如下:

密钥生成算法:

总体来说这一步的目的就是生成私钥
s
k
=
(
1
,
s
)
,
p
k
=
(
b
=
−
a
s
+
e
,
a
)
,
e
v
k
=
(
b
′
=
−
a
′
s
+
e
′
+
P
s
2
,
a
′
)
sk=(1, s),pk = (b=-as+e,a),evk=(b'=-a's+e'+Ps^2,a')
sk=(1,s),pk=(b=−as+e,a),evk=(b′=−a′s+e′+Ps2,a′)(这里的
a
,
a
′
a,a'
a,a′等等的取值分布是不一样的)
加密与解密
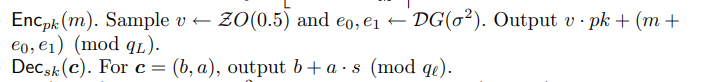
这里
c
=
v
⋅
p
k
+
(
m
+
e
0
,
e
1
)
=
(
b
⋅
v
+
m
+
e
0
,
a
⋅
v
+
e
1
)
c=v \cdot pk + (m+e_0,e_1)=(b\cdot v+m+e_0,a\cdot v+e_1)
c=v⋅pk+(m+e0,e1)=(b⋅v+m+e0,a⋅v+e1)
可以验证一下解密正确性:
<
c
,
s
k
>
=
<
(
b
⋅
v
+
m
+
e
0
,
a
⋅
v
+
e
1
)
,
(
1
,
s
)
>
=
m
+
e
⋅
v
+
e
0
+
e
1
⋅
s
≈
m
\begin{aligned} <c,sk> &=<(b\cdot v+m+e_0,a\cdot v+e_1),(1,s)>\\ &= m+e\cdot v + e_0+e_1 \cdot s\\ &\approx m \end{aligned}
<c,sk>=<(b⋅v+m+e0,a⋅v+e1),(1,s)>=m+e⋅v+e0+e1⋅s≈m
可以看到误差噪声是很小的。
注意,原文这里的算法应该是使用了BFV中的LPR方案作为基准,即解密结构为
c
0
+
c
1
⋅
s
c_0 +c_1\cdot s
c0+c1⋅s
所以原文中的
b
=
c
0
=
b
⋅
v
+
m
+
e
0
,
a
=
c
1
=
a
⋅
v
+
e
1
b=c_0= b\cdot v+m+e_0,a=c_1=a\cdot v+e_1
b=c0=b⋅v+m+e0,a=c1=a⋅v+e1。这样解密才正确(我感觉应该是作者有点符号串用?tmd😡)
同态运算与重线性化
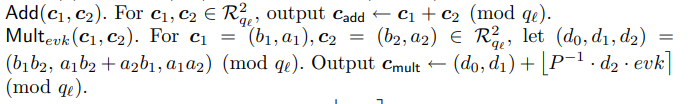
- 加法:对于加法没什么好说的,误差噪声就是和
- 乘法:
我们知道,密文乘法的时候会导致密文扩张,假设是两个密文相乘,那么乘积密文就会由两项变为三项,多次乘法后将会继续扩大,为了遏制这种扩张,这里采用了重线性化方法(有点类似BV11和BFV中的结合体)增加了一个修补项,目的就是把三项重新化为二项,代价就是会增加一点噪声。
先看看密文乘积解密
D
e
c
(
c
1
)
⋅
D
e
c
(
c
2
)
=
(
b
1
+
a
1
⋅
s
)
(
b
2
+
a
2
⋅
s
)
=
b
1
b
2
+
(
a
1
b
2
+
a
2
b
1
)
⋅
s
+
a
1
a
2
⋅
s
2
=
d
0
+
d
1
⋅
s
+
d
2
⋅
s
2
\begin{aligned} Dec(c_1)\cdot Dec(c_2) &= (b_1+a_1 \cdot s)(b_2+a2\cdot s) \\ & = b_1b_2+(a_1b_2+a_2b_1)\cdot s + a_1a_2\cdot s^2 \\ & = d_0+d_1 \cdot s +d_2 \cdot s^2 \end{aligned}
Dec(c1)⋅Dec(c2)=(b1+a1⋅s)(b2+a2⋅s)=b1b2+(a1b2+a2b1)⋅s+a1a2⋅s2=d0+d1⋅s+d2⋅s2
再来看看修补项的作用
<
P
−
1
⋅
d
2
⋅
e
v
k
,
s
k
>
=
P
−
1
⋅
d
2
⋅
b
′
+
P
−
1
⋅
d
2
⋅
a
′
⋅
s
=
d
2
(
P
−
1
⋅
e
′
+
s
2
)
≈
d
2
⋅
s
2
\begin{aligned} <P^{-1} \cdot d_2 \cdot evk,sk> &= P^{-1}\cdot d_2\cdot b'+P^{-1}\cdot d_2 \cdot a' \cdot s \\ &= d_2(P^{-1}\cdot e'+s^2) \\ &\approx d_2 \cdot s^2 \end{aligned}
<P−1⋅d2⋅evk,sk>=P−1⋅d2⋅b′+P−1⋅d2⋅a′⋅s=d2(P−1⋅e′+s2)≈d2⋅s2
由于
P
P
P是一个大数,所以这里的误差就很小,就能近似的将三项化为二项。
重缩放
先回想一下,我们在消息编码中乘以了一个缩放因子
Δ
\Delta
Δ,作用是提高精度。假定编码后的消息为
E
c
d
(
m
)
=
⌊
Δ
m
⌉
Ecd(m) = \lfloor \Delta m \rceil
Ecd(m)=⌊Δm⌉,那么在乘法计算中将得到
E
c
d
(
m
1
)
⋅
E
c
d
(
m
2
)
=
Δ
⋅
E
c
d
(
m
1
m
2
)
Ecd(m_1) \cdot Ecd(m_2) = \Delta \cdot Ecd(m_1m_2)
Ecd(m1)⋅Ecd(m2)=Δ⋅Ecd(m1m2),可以看到消息是被放大了的,所以要将其还原,就需要乘以一个
1
/
Δ
1/\Delta
1/Δ。另外,这个还有一个作用就是,能够缩小噪声。
这也表明CKKS支持的是定点的近似运算。

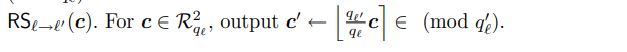
前面我们也提到了,模数链为
q
l
=
q
0
⋅
p
l
=
q
0
⋅
p
1
p
2
…
p
l
q_l=q_0 \cdot p^l = q_0 \cdot p_1p_2\dots pl
ql=q0⋅pl=q0⋅p1p2…pl,其中把
q
i
≈
Δ
q_i \approx \Delta
qi≈Δ,这样
q
l
′
/
q
l
≈
1
/
Δ
q_{l'}/q_l \approx 1/\Delta
ql′/ql≈1/Δ,就能达到还原明文的同时,进一步减少误差。
当然,方案的深度就受制于模数链了,做一次乘法就会消耗一个
q
i
q_i
qi。(和BGV中模切换一样)
参考
CKKS同态加密算法简介
全同态加密:CKKS
同态加密:CKKS方案详解及一个python实现:TenSEAL(不定期更新)
CKKS explained series
十分简明易懂的FFT(快速傅里叶变换)
Jung Hee Cheon, Andrey Kim, Miran Kim, and Yongsoo Song. 2017. Homomorphic encryption for arithmetic of approximate numbers. In Int’l Conf. on the Theory and Application of Cryptology and Information Security. Springer, 409–437



![[go学习笔记.第十六章.TCP编程] 2.项目-海量用户即时通讯系统](https://img-blog.csdnimg.cn/2615930efa4a4fb8b364542977b22152.png)