事件间的关系

• 注意互斥关系和对立关系：

  • 互斥关系是：只要 $A,B$ 不同时发生（不存在公共样本点）即可
  • 对立关系的要求更强：要求不仅 $A,B$ 不同时发生，而且 $A+B=S$ ，表示为 $A=\bar{B},B=\bar{A}$

• 多组事件之间的互不相容关系的表示
  

事件间的运算

• 因为之前说过事件就是集合，因此如果两个事件取 并集 $\cup$，就代表这个事件的范围变大了，比如掷骰子的点数的样本空间 S = { 1 , 2 , 3 , 4 , 5 , 6 } S=\{1,2,3,4,5,6\} S={1,2,3,4,5,6} ，获得奇数点数的随机事件 A = { 1 , 3 , 5 } A=\{1,3,5\} A={1,3,5}, 获得偶数的随机事件 B = { 2 , 4 , 6 } B=\{2,4,6\} B={2,4,6} 那么获得奇数或者偶数的随机事件 C = A + B = { 1 , 2 , 3 , 4 , 5 , 6 } = S C=A+B=\{1,2,3,4,5,6\}=S C=A+B={1,2,3,4,5,6}=S
• 交集运算，当然只存在于 $A,B$ 同时发生的时候。
• $A-B=\overline{A\cap B}$
  
  

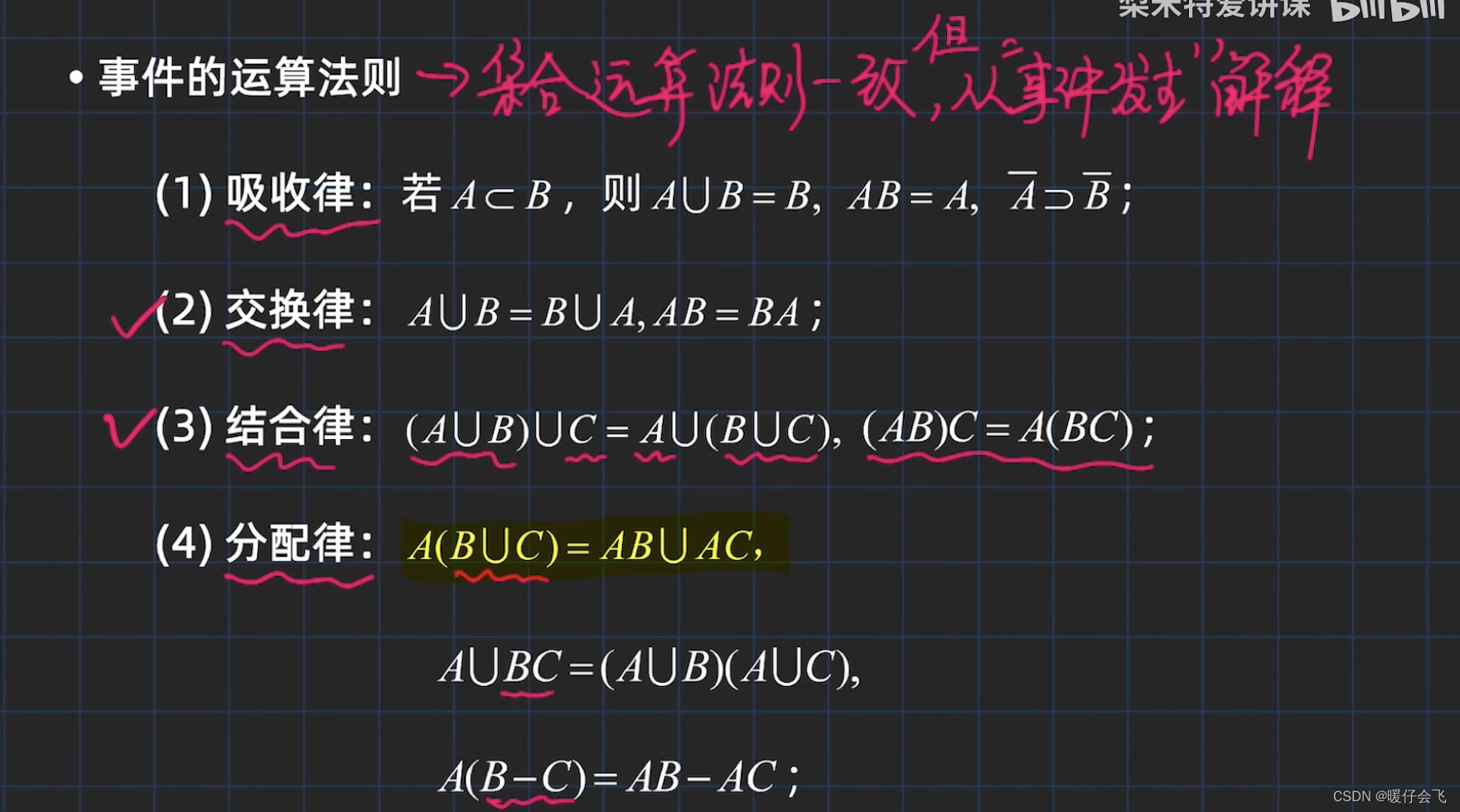
事件间的运算法则

概率

描述性定义

• 一个随机事件 $A$ 发生的可能性度量（非负）

统计性定义

频率

• 在相同的条件下进行了 $n$ 次实验，其中事件 $A$ 发生的次数是 $n_A$ 那么 $n_A$ 称为事件 $A$ 发生的频数，$\frac{n_A}{n}$ 称为事件 $A$ 发生的频率，记作 $f_n(A)$

频率的性质

• 事件 $A$ 发生的频率 $f_n(A)$ 在 $[0,1]$ 之间
• $f_n(S)=1$
• 对于 $N$ 个互不相容的事件 $A_1,A_2,...,A_N$ 有：$f(A_1\cup A_2\cup ,...,A_N)=f(A_1)+f(A_2)+,...,f(A_N)$

频率是否能够作为概率呢？

• 不同的人做同一个实验，一个事件出现的频率可能是不同的，比如张三抛100次硬币，正面出现的频率为 $0.55$，李四则是 $0.53$。
• 我们又知道，概率是一个定值，是一个客观的数据
• 但是当实验的基数够大的时候，即 $n\to \infty$ 的时候，频率会稳定到一个数值
• 但是有些实验（比如灯泡损坏的概率）是不可操作的，不能够进行足够多的实验，
• 这也就迫使数学家对概率进行公理化的定义

公理化定义

• 只要满足这三条性质，就是 概率。

概率的重要性质

• $P(\varnothing )=0$
• $A$ 发生 $B$ 不发生的概率：$P(A-B)=P(A\overline{B})=P(A)-P(AB)$
• 单调性： 如果 $B\subset A$ 则 $B$ 发生的时候 $A$ 一定发生并且 $P(A-B)=P(A)-P(B)$ ，而且 $P(A)\ge P(B)$
• 有界性： $P(A)\le 1$
• 逆事件概率： $P(\overline{A})=1-P(A)$
• 加法公式： $P(A\cup B)=P(A)+P(B)-P(AB)$