目录

343. 整数拆分

思路

整数拆分

96.不同的二叉搜索树

思路

不同的二叉搜索树

---

343. 整数拆分

题目链接：力扣

思路

        动态规划的题目虽然说是要先确定dp数组的含义，再确定递归公式，但是总感觉这两者是相辅相成的，是一起出来的，但是到此，dp数组代表的都是我们要求取的值

1、确定dp数组以及下标的含义

        i 代表dp数组的下标和 要被拆分的数字
        dp[i] 代表数字 i ,被拆分后相乘可以得到的最大值

2、确定递推公式

        获取递归公式要推导清楚，dp[i] 是怎么来的

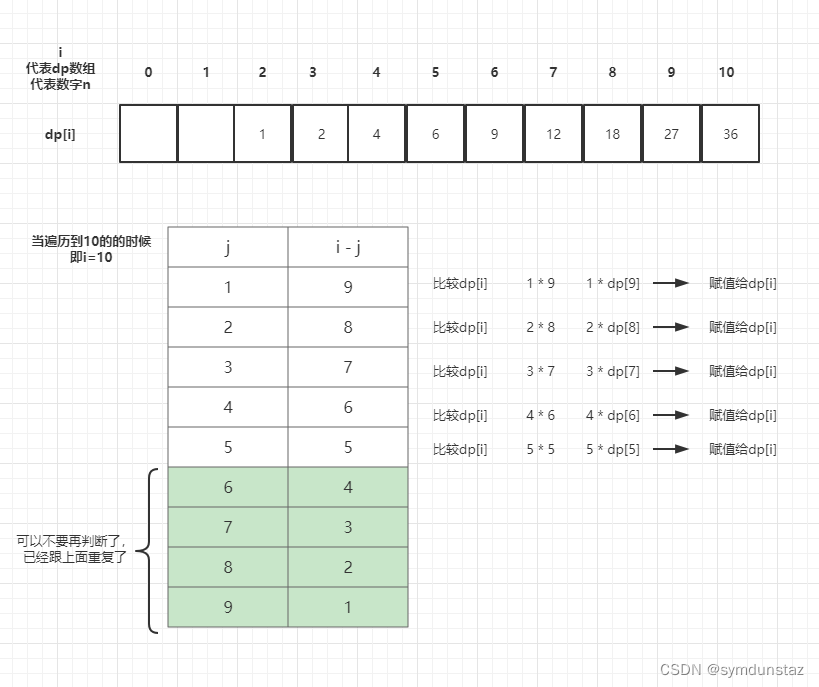
        比如，现在的数字是10，进行拆分
        【1，9】【2，8】【3，7】【4，6】【5，5】后面的都会和前面重复，所以拆到5就可以了
        那么其实从 1 遍历，就可以获得dp[i] 可以通过 j * (i - j)进行获取

        还有就是后面得到的这个数组还可以进行拆分，比如【9、8、7、6、5】，这里就可以借助dp[]数组前面的元素了【9的拆分、8的拆分、7的拆分、6的拆分、5的拆分】，其实就是dp[9]、dp[8]、dp[7]……加一句：从这里也可以看到一点就是，遍历顺序应该是从前先后的，因为后面的拆分要使用前面数字的结果
        所以dp[i] 还可以通过 j * dp[i - j]进行获取

        总的来说 dp[i] = Math.max(dp[i] , j * (i - j) , j * dp[i - j]);

3、dp数组初始化

        对于初始化数组来说，dp[0],dp[1] 严格意义上来说，0 和 1 是不可拆分的，他们拆分后的最大值是不存在的

        2是可以进行拆分成 1 和 1 的。所以赋值为1

4、确定遍历顺序

        从前向后遍历

        其中的 j 其实最大值为 i-j ，再大只不过是重复而已
        并且本题中的 dp[0] , dp[1] 都是无意义的，j 最大值到达 i-j 。就不会用到 dp[0] 和 dp[1]

         j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ，再相乘
         而j * dp[i - j]是将 i 拆分成两个以及两个以上的个数,再相乘

5、打印dp数组

 

整数拆分

class Solution {
    public int integerBreak(int n) {

        // 创建dp数组
        int[] dp = new int[n + 1];

        // 初始化数组
        dp[2] = 1;

        // 填充dp[]数组
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j <= i - j; j++) {
                dp[i] = Math.max(dp[i],Math.max( j * (i - j) , j * dp[i - j]));
            }
        }

        return dp[n];
    }
}

96.不同的二叉搜索树

题目链接：力扣

思路

        这道题目发现递推公式真的是太难了

1、定义dp[] 数组

        dp[i] 代表，由 i 个节点组成且节点值从 1 到 i 互不相同的二叉搜索树有dp[i] 种

2、递推公式

        很难发现的一种，至少要将前面三个画出来才可以发现出规律，可以推出：
        dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
        j相当于是头结点的元素，从1遍历到i为止
        所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量

3、初始化

        初始化，只需要初始化dp[0]就可以了，推导的基础，都是dp[0]
        初始化dp[0] = 1

4、遍历顺序

        从小到大遍历

5、打印dp数组

不同的二叉搜索树

class Solution {
    public int numTrees(int n) {

        // 定义dp[]数组
        int[] dp = new int[n + 1];

        // 初始化dp数组
        dp[0] = 1;
        
        // 填充dp数组
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }

        }

        return dp[n];
    }
}