这篇记录一下刷接雨水这道题的过程,日后回顾
目录
法1:
法2:
法3:
法4:
法5:
务必掌握123
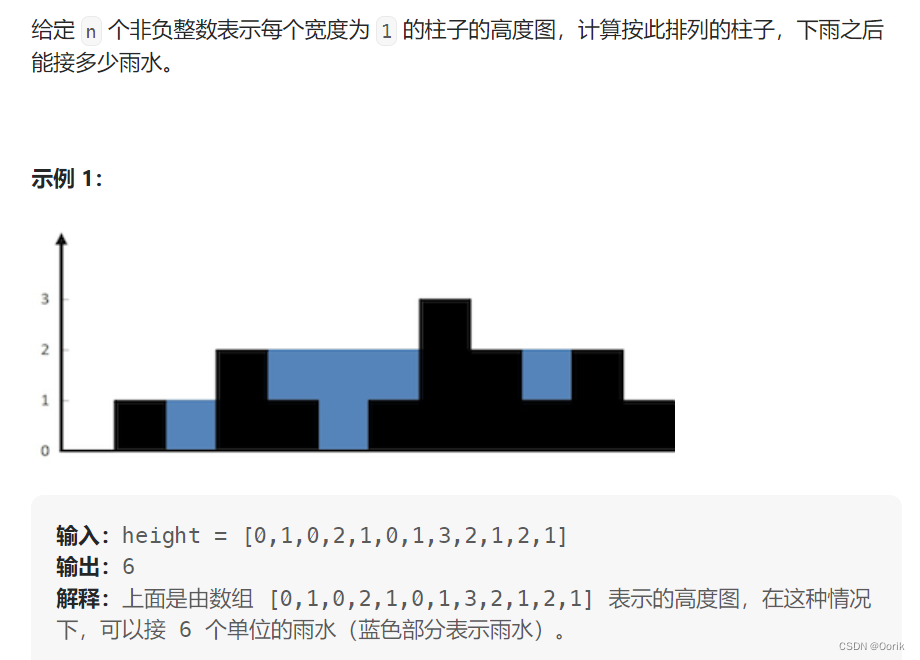
写这道题要知道雨水怎么算。核心就是要算当前列雨水的高度就要取决于这列左右两侧比自己搞得柱子中较矮的那一个柱子
当前列雨水面积:min(左边柱子的最高高度,记录右边柱子的最高高度) - 当前柱子高度。
你要能接水说明你得是个凹才可以,比如上面第一个雨水,那一列是空的左边高度是1,右边是2,取个最小的减去当列的高度,就是你当列能接多少水

那么第一种方法就出来了,暴力去找每一列的两侧的那个高柱子,就去计算雨水,然后把每次计算的雨水累加就行
法1:
class Solution {
public:
int trap(vector<int>& height) {
int sum = 0;
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i == 0 || i == height.size() - 1) continue;
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
//两边高柱子的小的减去当前列,计算雨水
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h;
}
return sum;
}
};这么写的话我试了,在力扣上跑不过去,时间复杂度是on2,因为要遍历每一列两边的最高柱子,相当于每走一次就要向两边去探测

法2:
下面解决方法就是降低复杂度了,因为思路是没问题的,下面这种方法可以复杂度降低到on,不空空间上又成了on,用用备忘录或者说就是动态规划
怎么去优化呢?
上面我们每一次都要去计算一下当前列左右两边的最高柱子是谁,有很多重复计算,这下我们可以定义两个数组去记录一下每次左边最高的柱子和右边最高的柱子是谁,像备忘录一样
比如
使用两个数组 maxleft 和 maxright,maxleft[i] 表示下标 i 左边最高柱子的高度,maxright[i] 表示下标 i 右边最高柱子的高度,这样的话一次遍历就可以了,代价就是空间复杂度高了
代码示例:
class Solution {
public:
int trap(vector<int>& height) {
if(height.size()<=2)
{
return 0;
}
//记录每个柱子左边最高的柱子高度
vector<int>ml(height.size());
//同理右边
vector<int>mr(height.size());
int n=height.size();
ml[0]=height[0];
mr[n-1]=height[n-1];
//存到备忘录里
for(int i=1;i<n;++i){
ml[i]=max(height[i],ml[i-1]);//看看当前的和左边最高的谁高,ml存的就是每次最高的,如果2最高连着存进去,那么ml[i-1],ml[i-2]..都是2,都是最高的,这个要理解
}
for(int i=n-2;i>=0;--i)
{
mr[i]=max(height[i],mr[i+1]);
}
//开始算雨水
int sum=0;
for(int i=0;i<n;++i){
int tmp=min(ml[i],mr[i])-height[i];
if(tmp>0){
sum+=tmp;
}
}
return sum;
}
};法3:
在时间On的基础上,降低空间,把上面备忘录方法里两个数组用指针去代替操作一下,这就是双指针法,很巧妙
这个题双指针的话思路都是一样,就是实现上面很巧妙,我也是搞了很久才搞清楚
拿代码来说:
class Solution {
public:
int trap(vector<int>& height) {
int res=0;
int left=0,right=height.size()-1;
int n = height.size();
int l_max = height[0];
int r_max = height[n - 1];
while(left<right)//每次更新左右高度的最大值
{
l_max = max(l_max, height[left]);
r_max = max(r_max, height[right]);
// ans += min(l_max, r_max) - height[i]
if (l_max < r_max) {
res += l_max - height[left];
left++;
} else {
res += r_max - height[right];
right--;
}
}
return res;
}
};拆解一下代码思路:
1、定义两个指针 (左、右指针)
2、定义左、右的边界最大值,并在移动中更新这两个max(用于计算比他低的差值——也就是存水量)。
3、比较2个指针所在位置的高度,然后谁小谁先移动(左++,右-- 两边收紧模式)
4、移动的同时计算差值(谁小谁先动,另一边一定比他高所以不用担心漏的问题)
ps:左右边界在移动中 ,高度都取max,所以在递增情况时,max即当前值,total便不会增加。
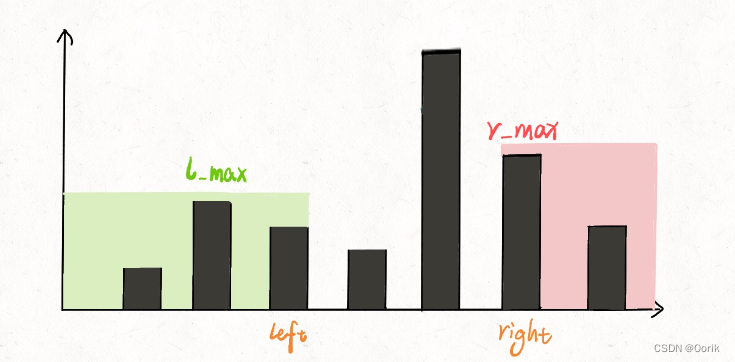
假设一开始lmax大于rmax,则之后right会一直向左移动,直到rmax大于lmax。在这段时间内right所遍历的所有点都是左侧最高点lmax大于右侧最高点rmax的,所以只需要根据原则判断rmax与当前高度的关系就行。反之left右移,所经过的点只要判断lmax与当前高度的关系就行。
有点类似快排的走法
对比上面备忘录,ml【i】记录的是0到 i的最高柱子,mr【i】是i到结尾的最高柱子
双指针里面
l_max和r_max代表的是height[0..left]和height[right..end]的最高柱子高度
对于这段代码
if (l_max < r_max) { res += l_max - height[left]; left++; }我们解释一下,为什么这样就可以去计算雨水了。
此时的 l_max 是 left 指针左边的最高柱子,但是 r_max 并不一定是 left 指针右边最高的柱子,这真的可以得到正确答案吗?
其实这个问题要这么思考,我们只在乎 min(l_max, r_max)。对于上图的情况,我们已经知道 l_max < r_max 了,至于这个 r_max 是不是右边最大的,不重要,重要的是 height[i] 能够装的水只和 l_max 有关。
法4:
写到这的时候又发现了个很牛的写法,不过照着代码走一遍就能懂为什么这么写了
看接完水的数字很像一个山峰,左边递增,右边递减(不严格的递增递减),那么久很好办了。找到这个找到最大值索引,左右各自遍历一遍 两边都维护一个值来表示之前的最大值以保证单调性, 如果比最大值小,雨水量就加上这个差值, 如果大于等于,就更新最大值。
- 先遍历一遍,找到最高点,记录高度imax和坐标h
- 再分别从两边两个指针往中间扫,以当前遍历中遇到的最高点的高度为标准stan
- 再往中间走,如果当前的坐标高度小于stan,就说明当前坐标能接的雨水为stan-height[i]
class Solution {
public:
int trap(vector<int>& height) {
if(height.size()==0) return 0;
int imax=-1,h;
for(int i=0;i<height.size();i++)//找到最高点和它的高度
{
if(height[i]>imax)
{
imax=height[i];
h=i;
}
}
int stan=0,ans=0;
for(int i=0;i<h;i++)//从前遍历到最高点
{
if(height[i]>stan)
{
stan=height[i];
continue;
}
else ans+=stan-height[i];
}
stan=0;//stan归零
for(int i=height.size()-1;i>h;i--)//从后遍历到最高点
{
if(height[i]>stan)
{
stan=height[i];
continue;
}
else ans+=stan-height[i];
}
return ans;
}
};
法5:
还有单调栈的写法这里就不写了
贴个题解日后回来看
42. 接雨水 - 力扣(Leetcode)