内容概要

1 三维数据的获取方式
2 三维数据的获取原理
3 三维信息的表征形式
4 深度学习中的三维表征
5 点云的基本特征和描述
6 三维空间变换

1 三维数据的获取方式及原理

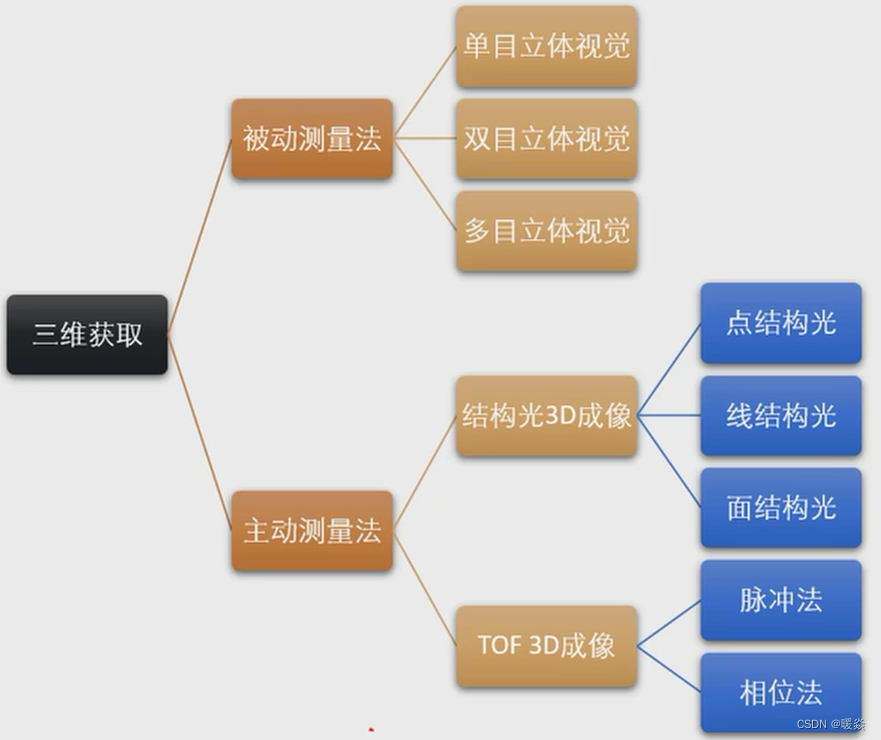
1.1 被动测量

单目立体视觉

双目立体视觉

多目立体视觉

1.2 主动测量

结构光3D成像

TOF 3D成像

脉冲法

相位法

2 三维数据的获取原理

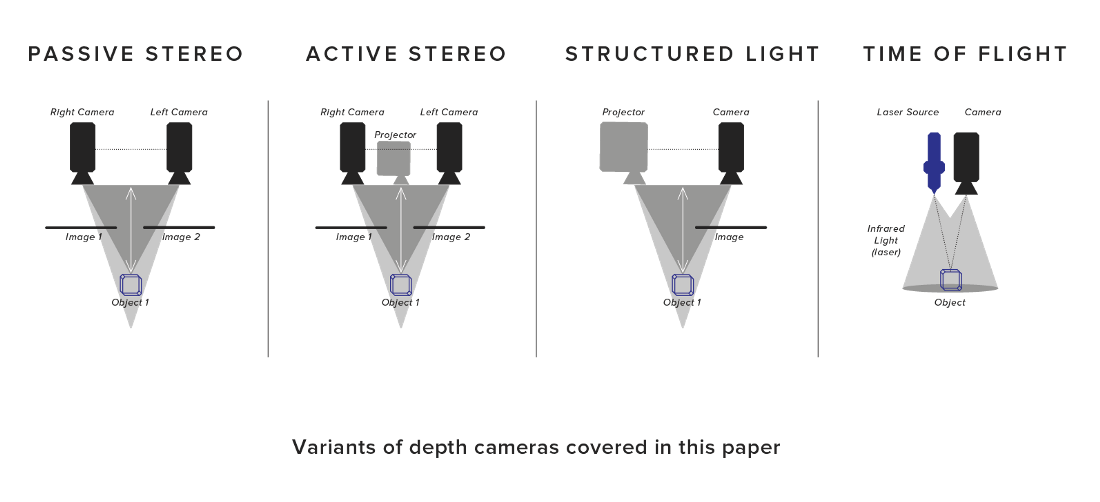
立体视觉测量法

相机成像模型

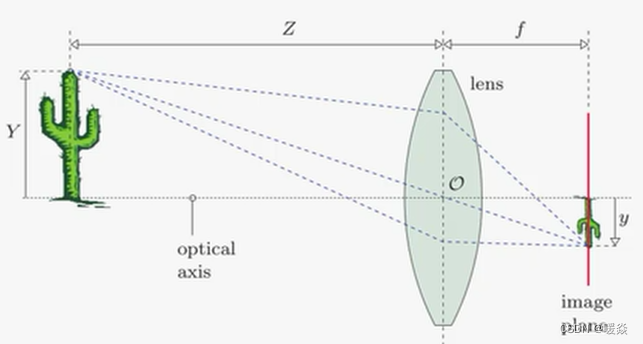
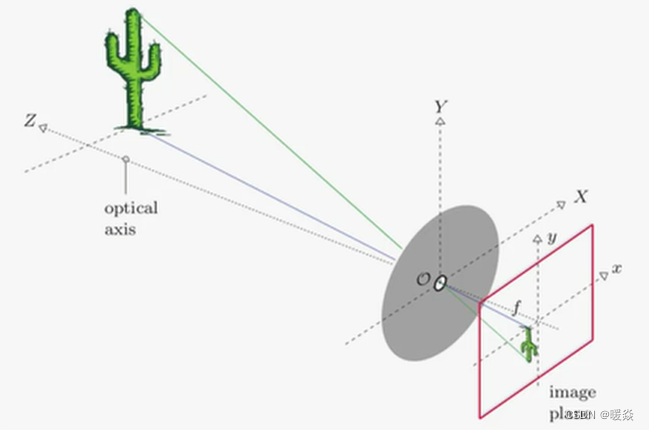
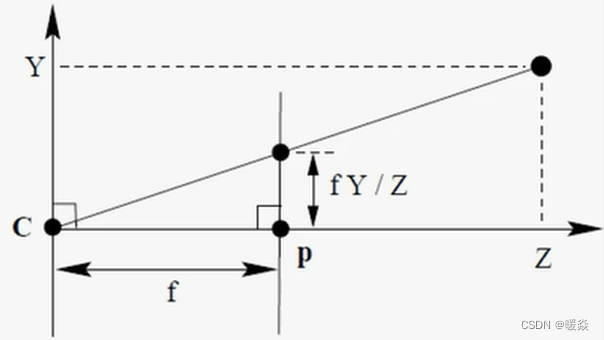
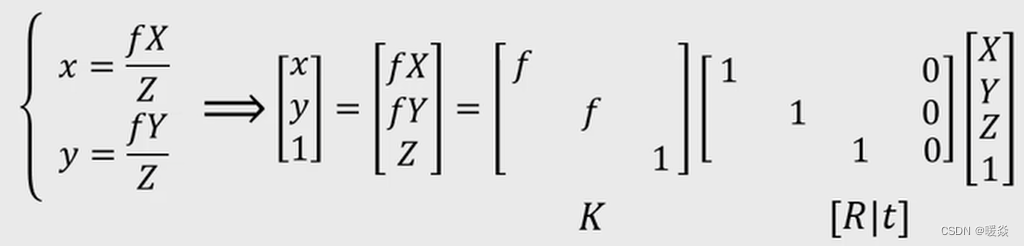
小孔成像模型（相机成像模型的理想情况）

小孔成像中没有畸变，但是在相机成像中，可能出现光心偏移或者透镜材质不均匀导致的畸变。

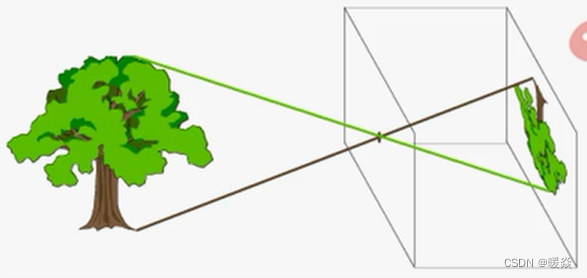
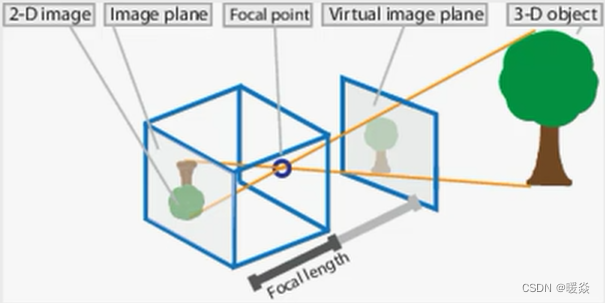
单目立体视觉

聚焦法

相机主动调焦，并使相机相对于被测点处于聚焦位置，然后根据透镜成像公式求得被测点相对于相机的距离。相机偏离聚焦位置会带来测量误差，因此寻求精确的聚焦位置是关键所在。

离焦法

不要求相机相对于被测点处于聚焦位置，而是根据标定出的离焦模型计算被测点相对于相机的距离，这样就避免了由于寻求精确的聚焦位置而降低测量效率的问题，但离焦模型的准确标定是该方法的主要难点。

单目棱镜法（变向实现多目）

主要应用于微观结果或光学研究。

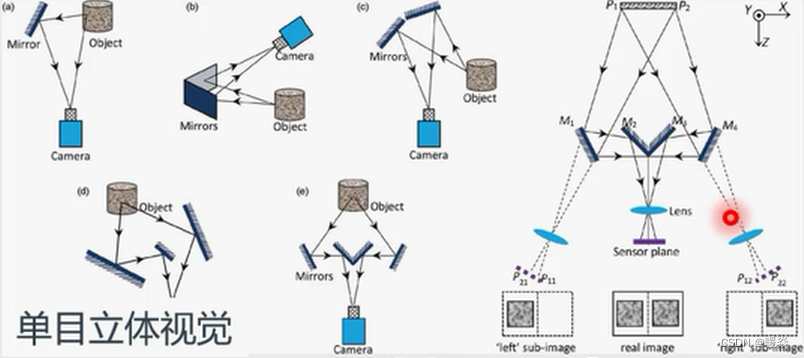
双目立体视觉

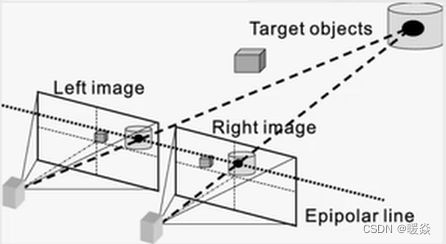
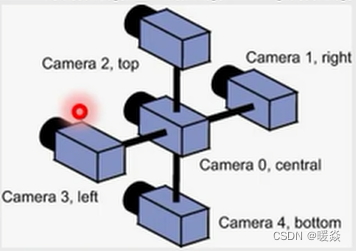
多目立体视觉

机器人系统里应用的多。

3 三维信息的表征形式

图片来源 http://graphics.stanford.edu/courses/cs468-17-spring/

点云 PointCloud

参数化曲线曲面 Parametric Surface

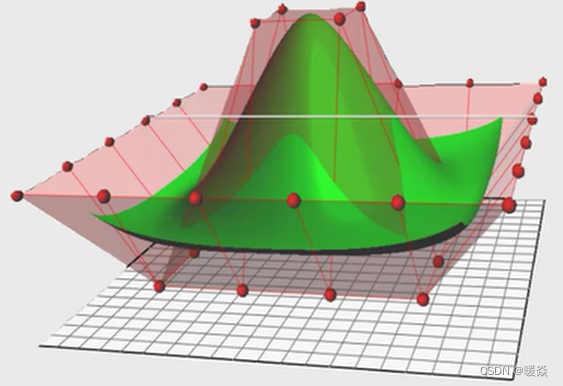
参数化曲线

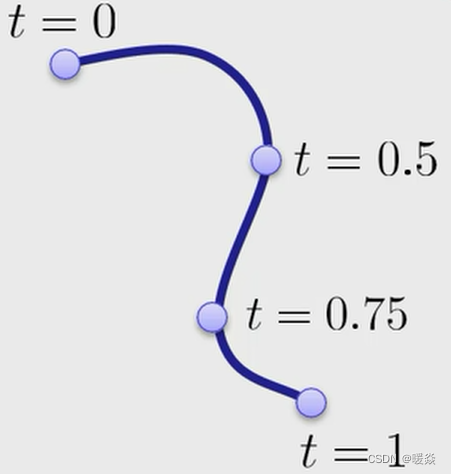
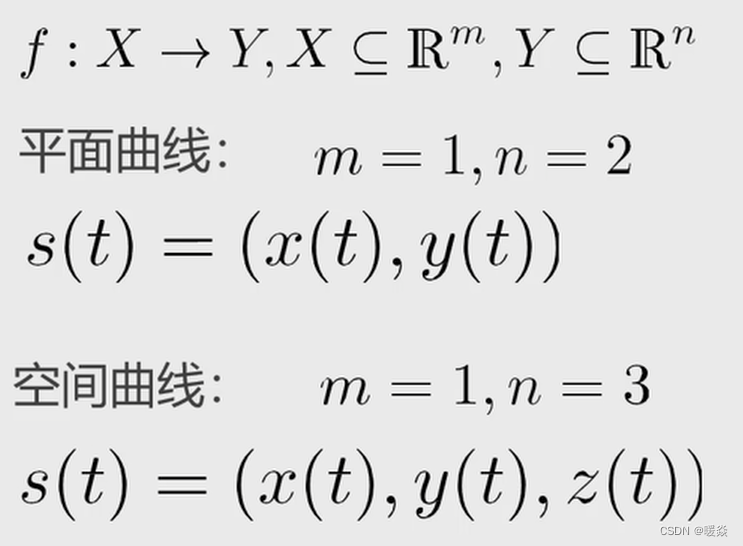
常用参数化曲线

贝塞尔曲线（应用：样条线）

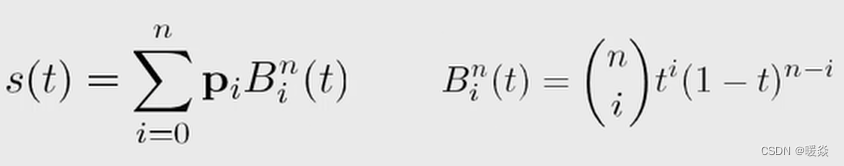
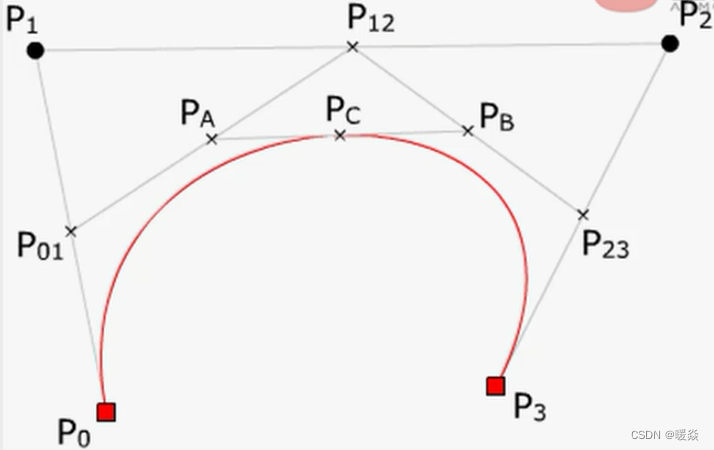
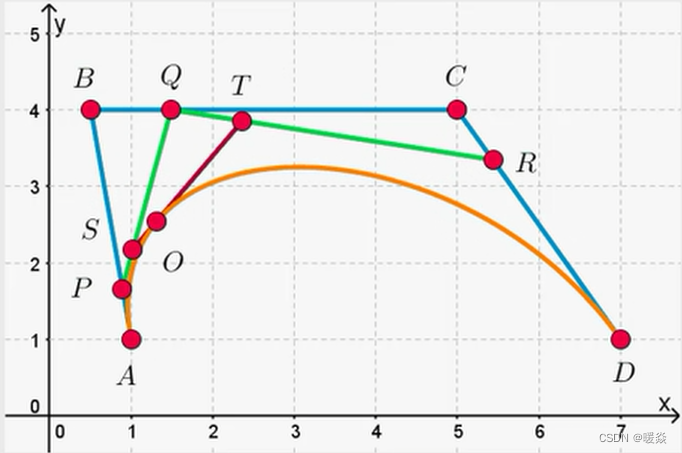
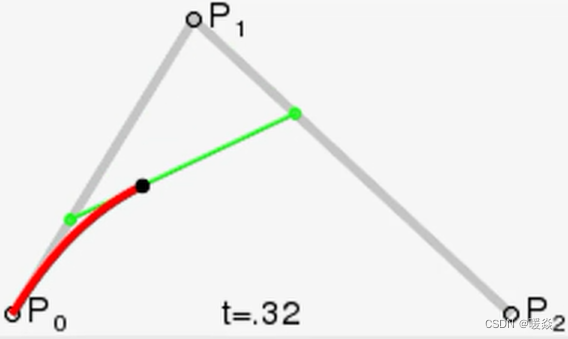
参数化曲面

参数化曲面表示

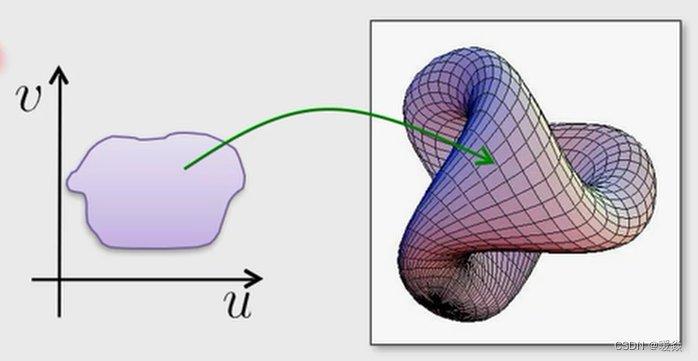
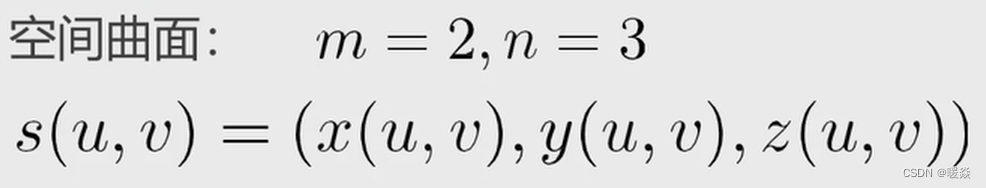
优点

容易生成曲线或者曲面上的点
参数分离，容易分析

缺点

难以确定内部外部空间
难以判断点是否在曲面曲线上
难以生成非常复杂的曲线曲面（解决：局部表面（多边形面元））

常见的参数化曲面

曲线扫描得到曲面

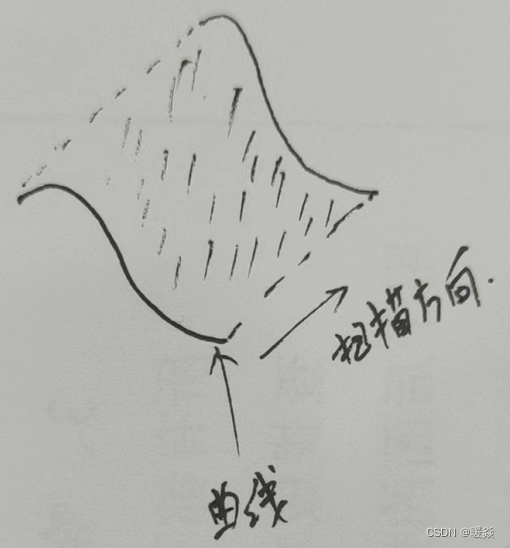
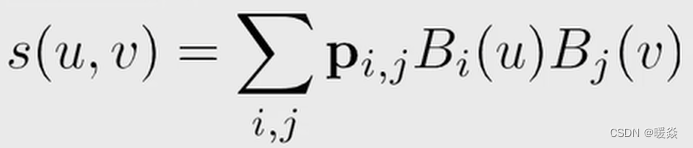
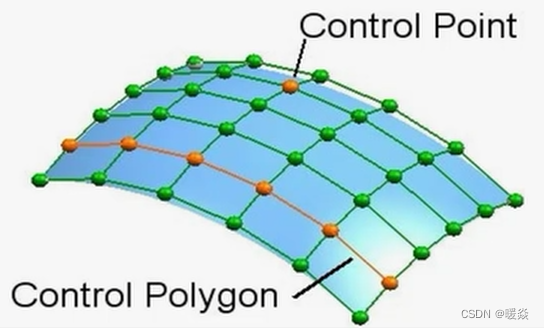
贝塞尔曲面

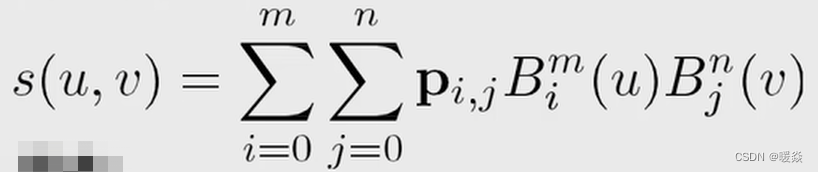
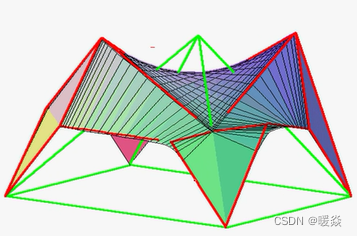
隐式曲线曲面 Implicit Surface

隐式曲面表示

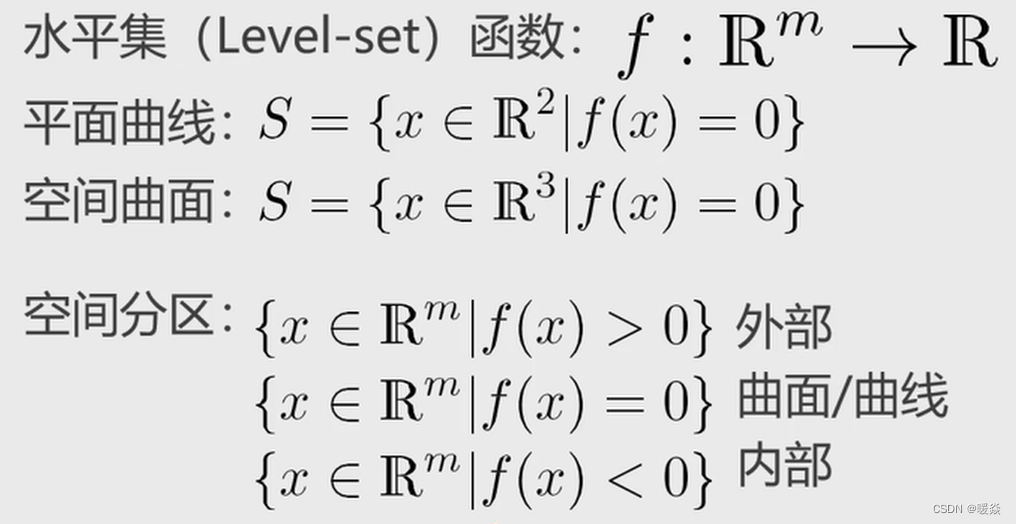
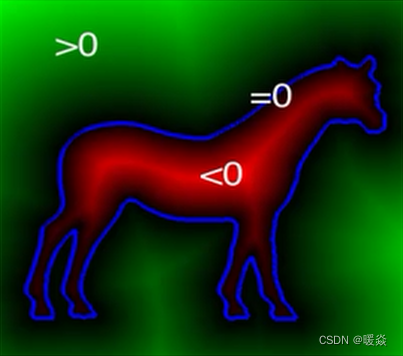
优点

容易确定内部外部空间
容易确定点是否在曲线曲面上

缺点

难以生成曲线曲面上的点
不适合实时渲染

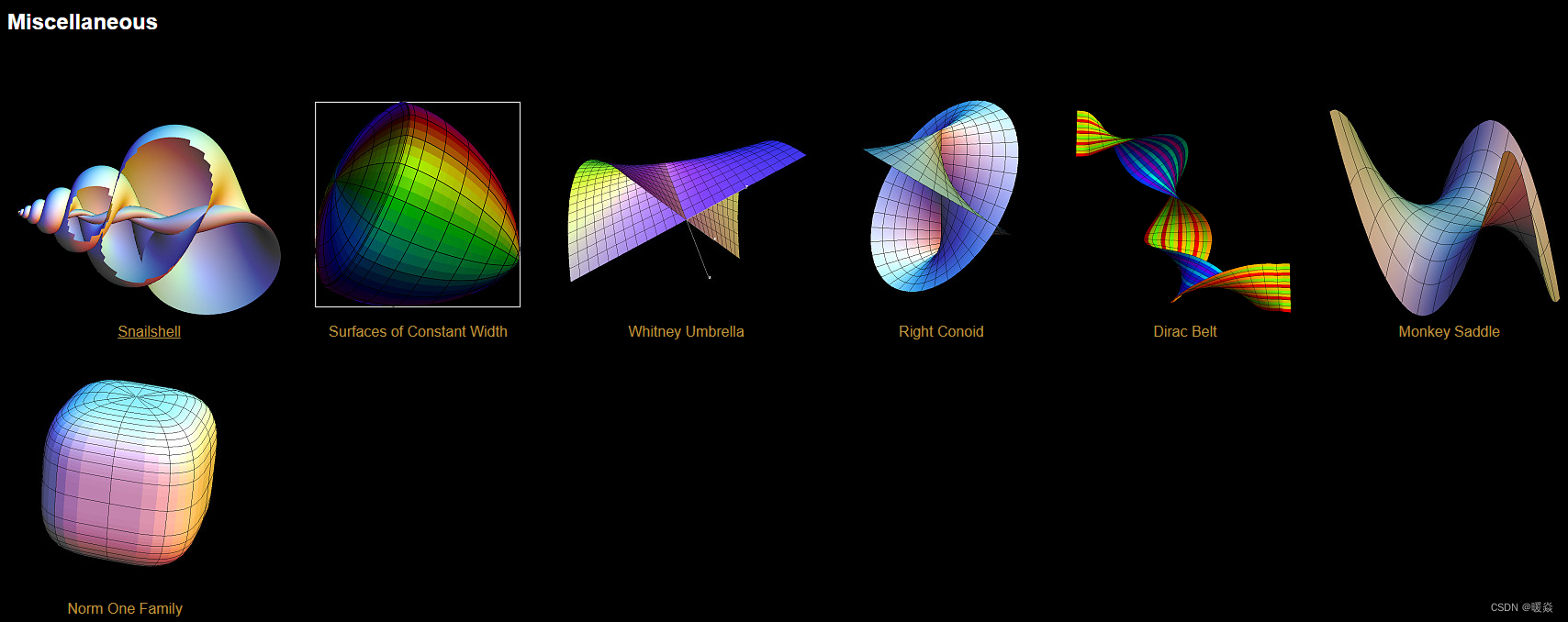
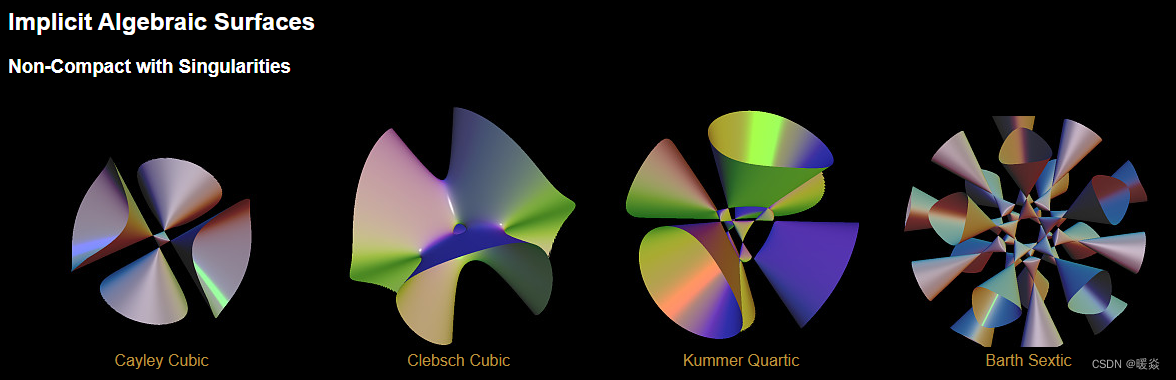
常见隐式曲面

图片来源：https://virtualmathmuseum.org/Surface/gallery_o.html

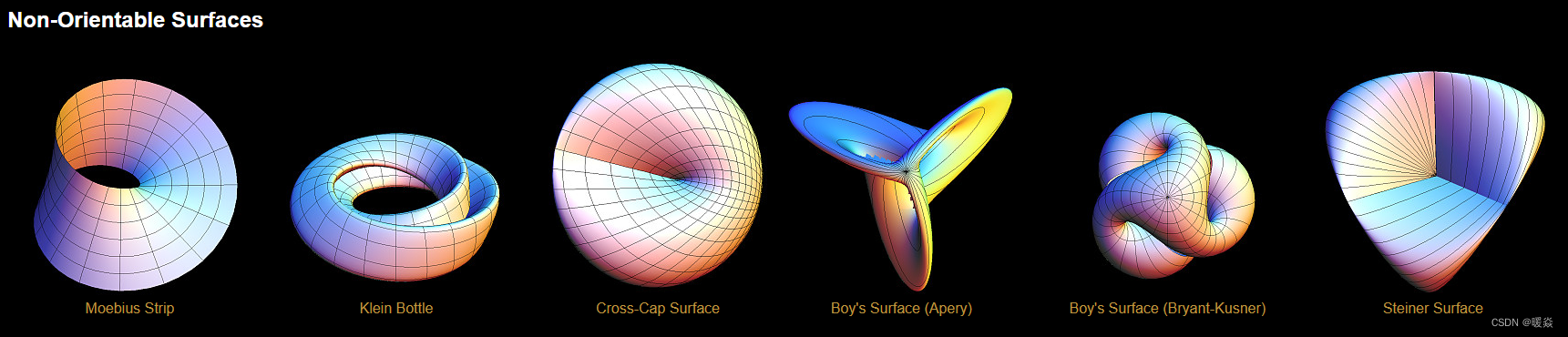
细分曲面 Subdivision Surface

多边形面元 Mesh

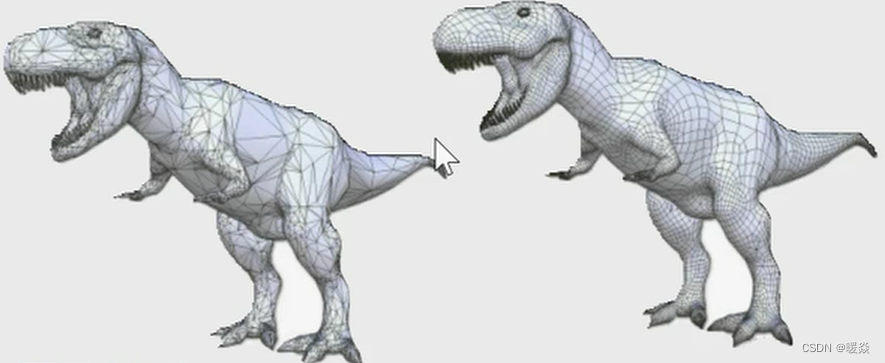
分的越精细拟合的越好。

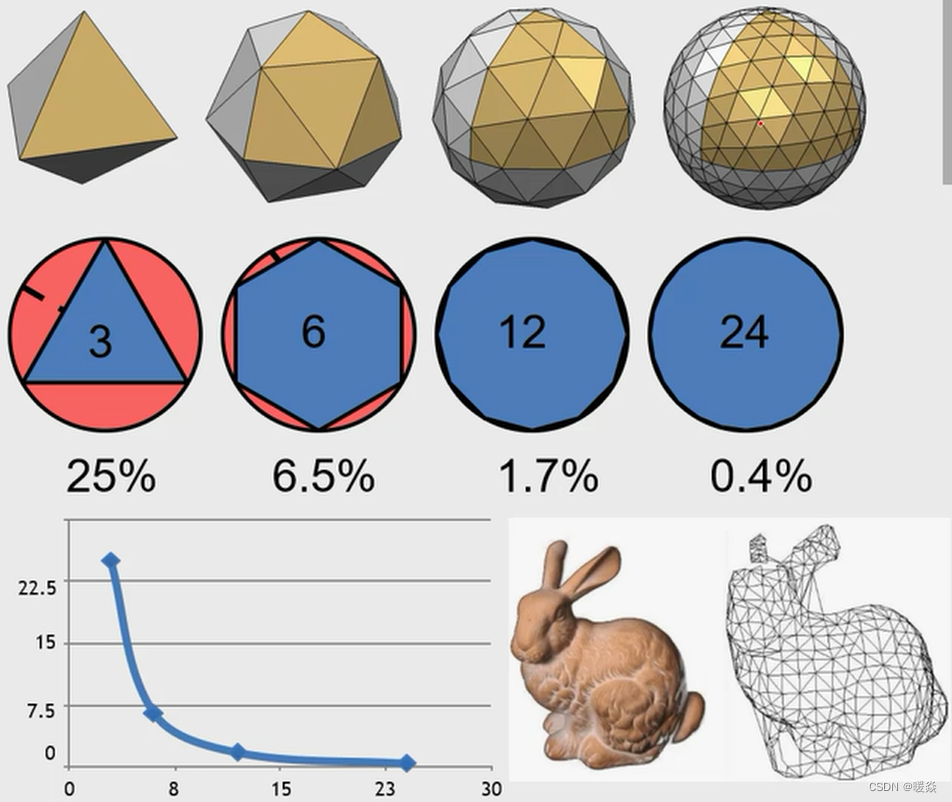
量化误差可控（分的越精细拟合的越好）
应用于任意拓扑结构
支持动态调整
可以利用GPU高效运算

常见多边形面元

多边形面元（多边形剖分）

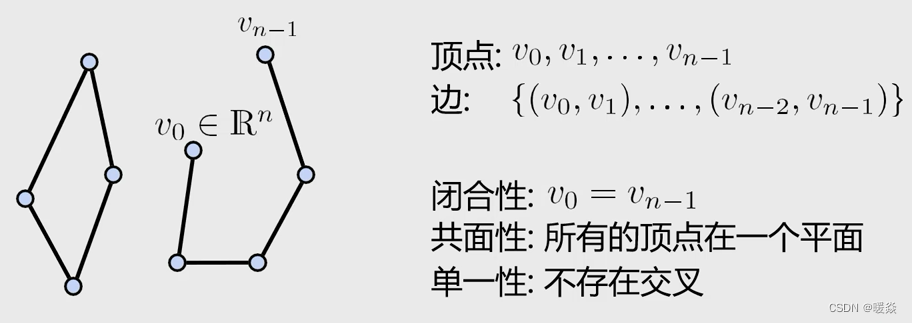
数学表征

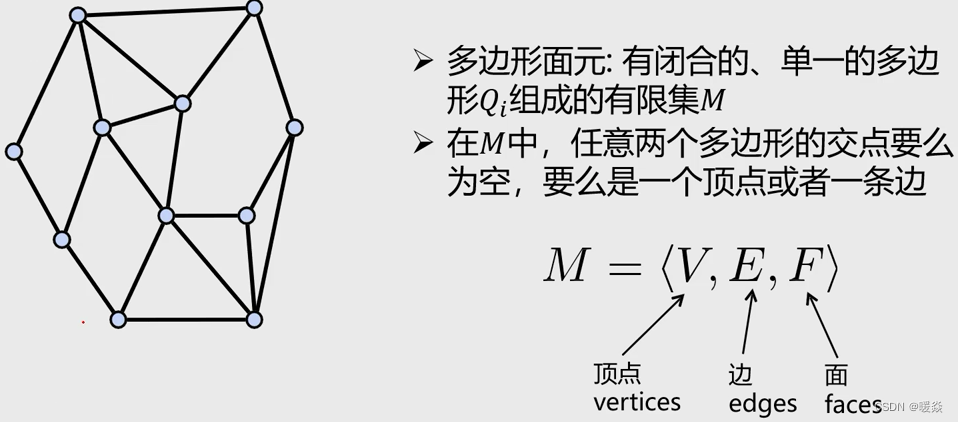
性质

每条边至少属于一个多边形。

每个Q_i定义了多边形网格的一个面。

顶点的度=入射边的数目

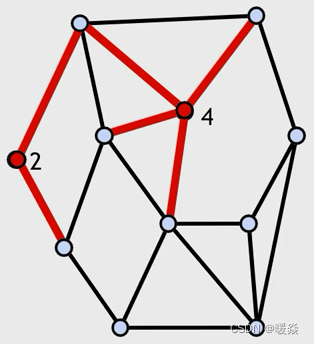
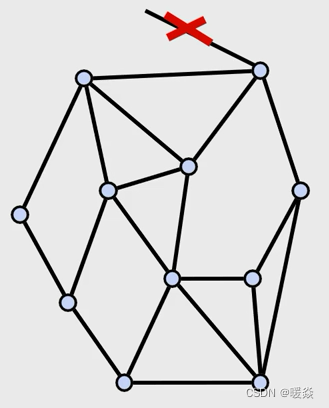
多边形面元的边界

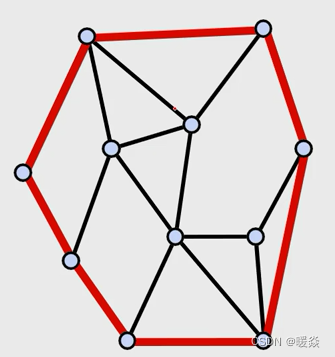
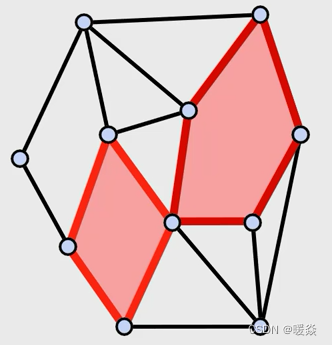
三角面元（三角剖分）

多边形面元，其中每个面是三角形。

数学表征

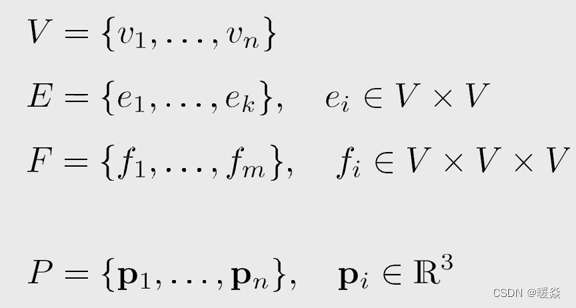
优点

简化数据结构
简化渲染
简化算法
每个面都是平面和凸的
任何多边形都可以三角化

如何将点云转换为面元？

delaunay 三角剖分准则

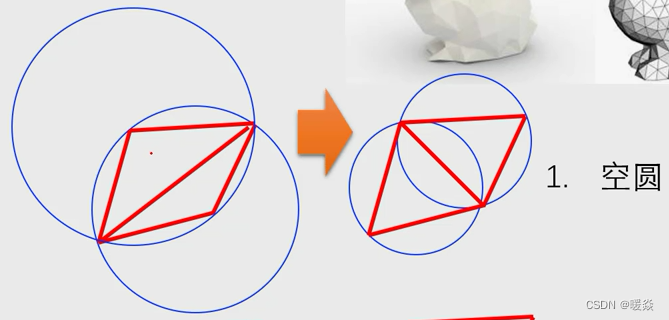
bowyer-watson 算法

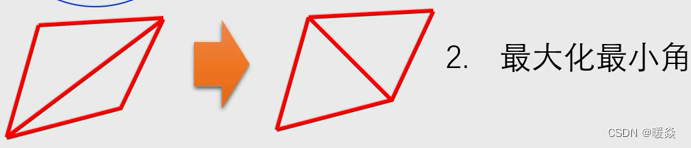
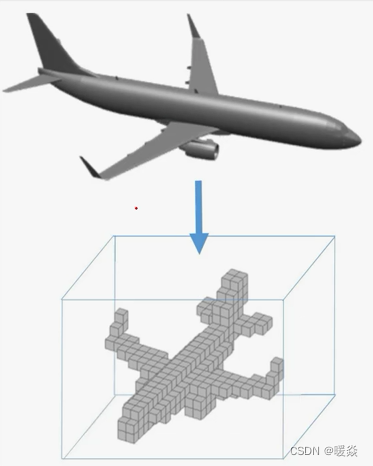
体素

无序点云有序化（类比像素）
空间体素化，占用格点0, 1（格子越小精度越高）

优点

快速检测空间点是否被占据
体像素之间的逻辑运算
运算速度快

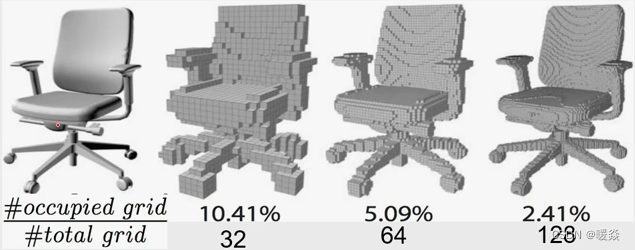
缺点

存储效率很低，特别在深度学习模型中问题突出。

4 深度学习中的三维表征

4.1 点云研究中的三维表征

4.2 自动驾驶研究中的三维表征

5 点云的基本特征和描述

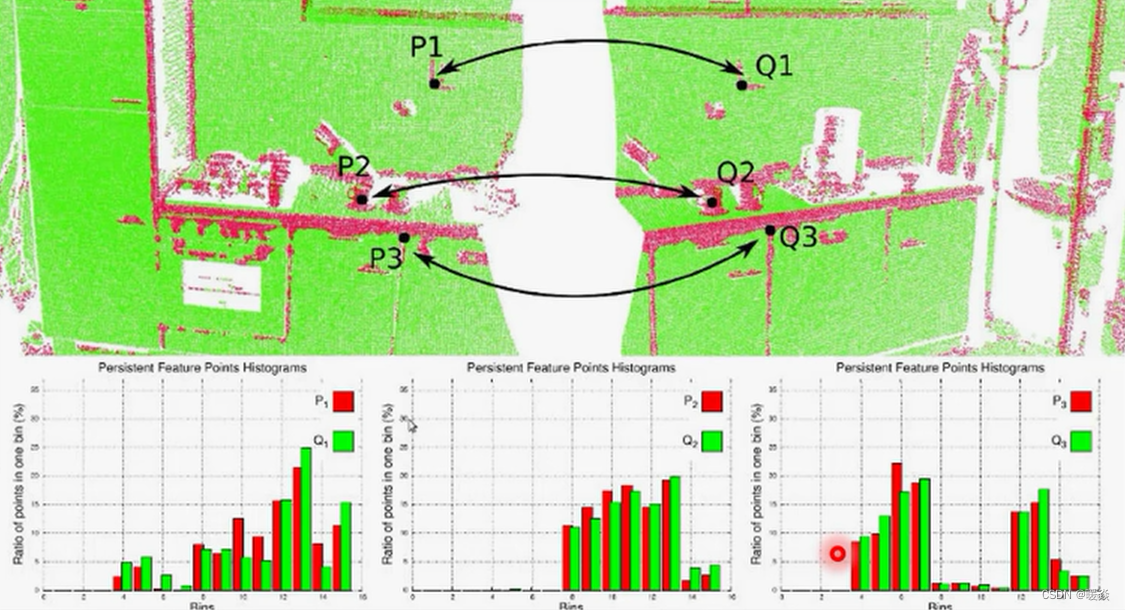
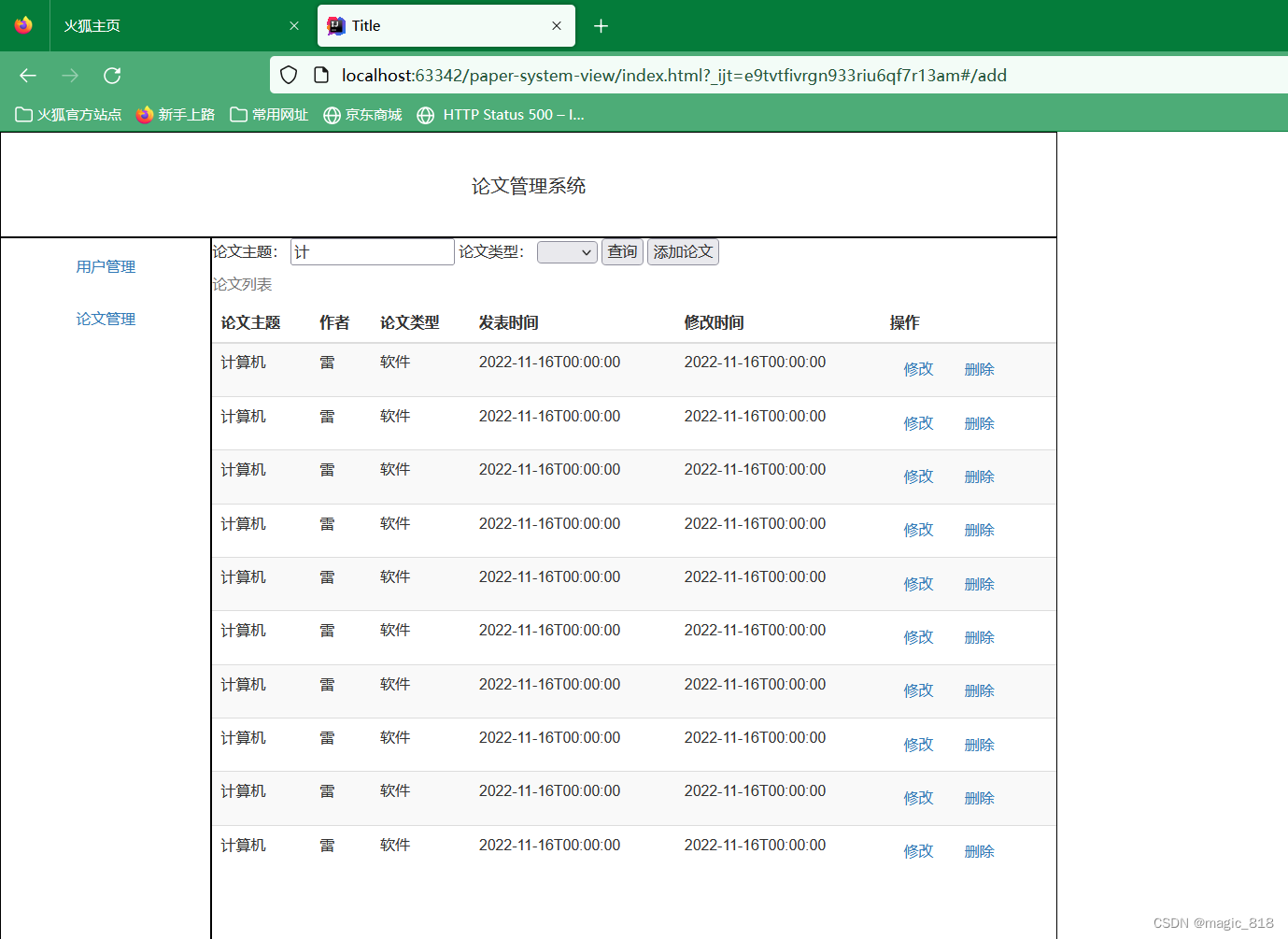
RGBD 两个不同视角下相比较，有相同有不同。

点云基本特征

按照特征的物理属性，可以将特征分为：几何域，强度域
按照特征的空间尺度，可以分为：单点特征，局部特征，全局特征

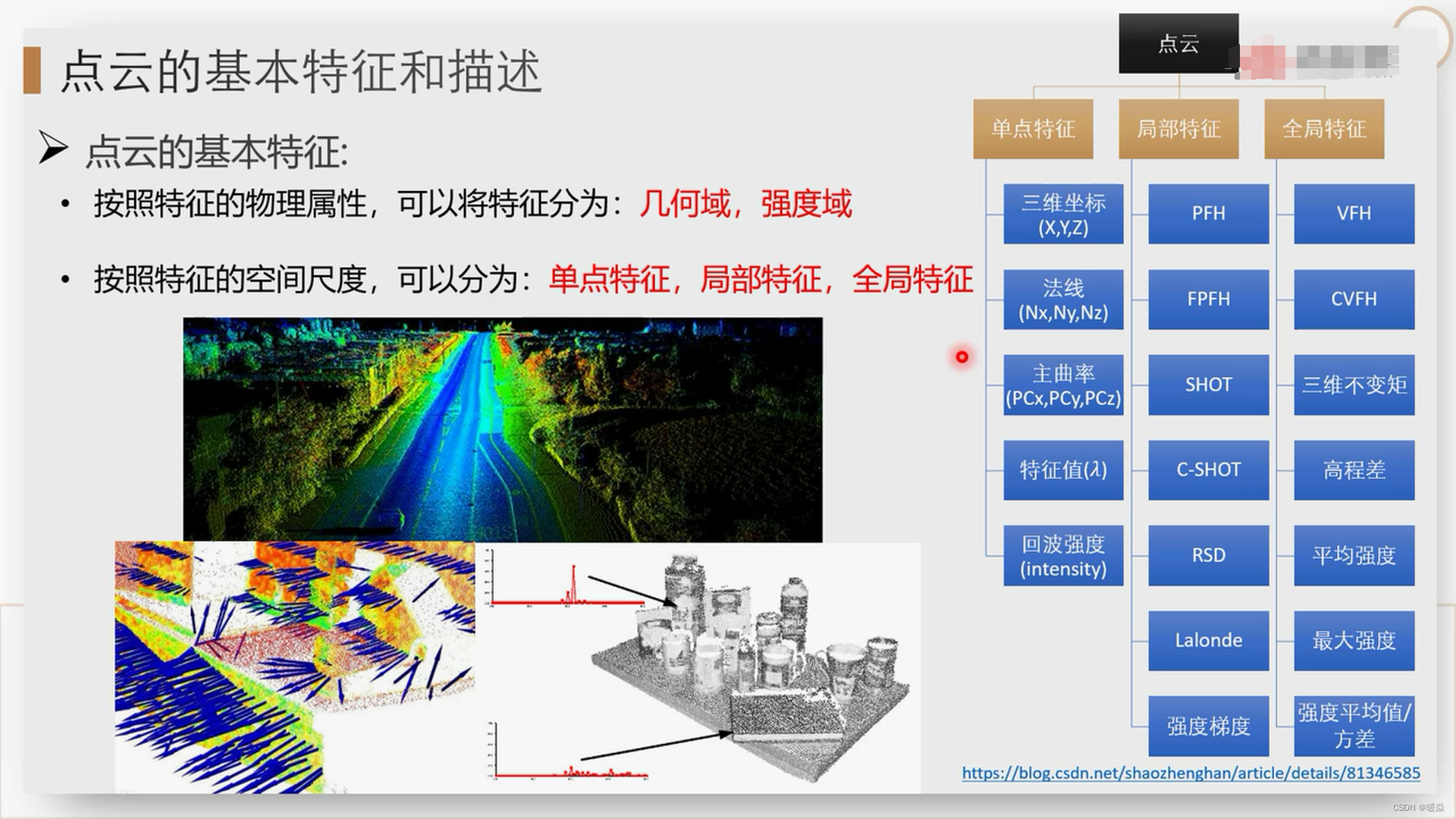
点云基本特征描述

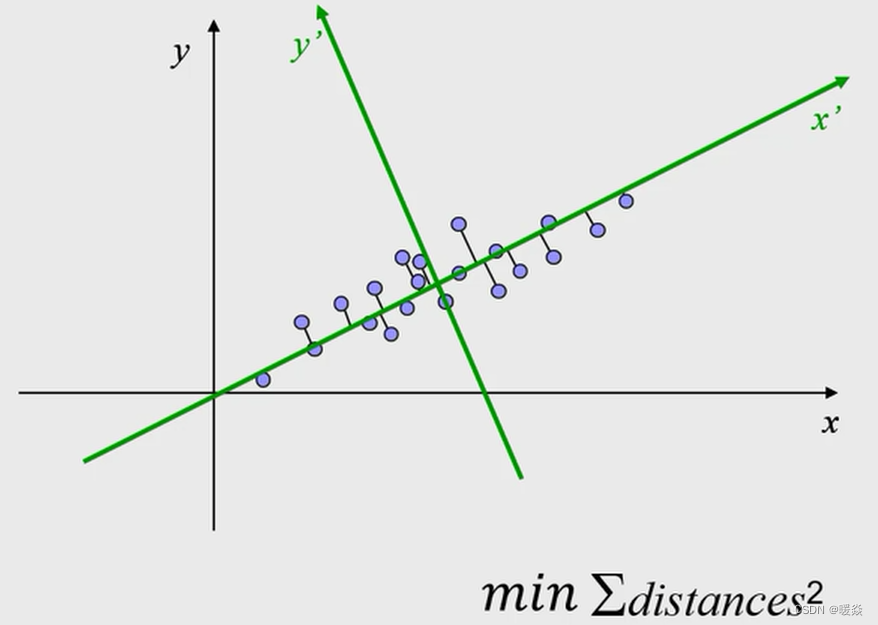
法向量