Matlab 对连续时间信号的运算

1、连续时间系统零状态响应

题目&函数说明
连续时间系统的微分方程为 y"(t) + 4y’(t) + 3y(t) = f’(t) + 2f(t)
当输入信号 f(t) = 20e^-2tu(t) 时，初始值 y(0^-) = 2, y’(0^-) = 1, 求系统的零状态响应

Matlab 库函数中的 lsim()能对微分方程描述的 LTI 连续时间系统的响应进行仿真。
函数 lsim()的调用格式： lsim(b,a,x,t)
该调用格式中，a 和 b 是由描述系统的微分方程左边和右边系数构成的两个行向量；t 为输入信号时间范围的向量，x 为输入信号在向量 t 定义的时间点上的抽样值。

结果：

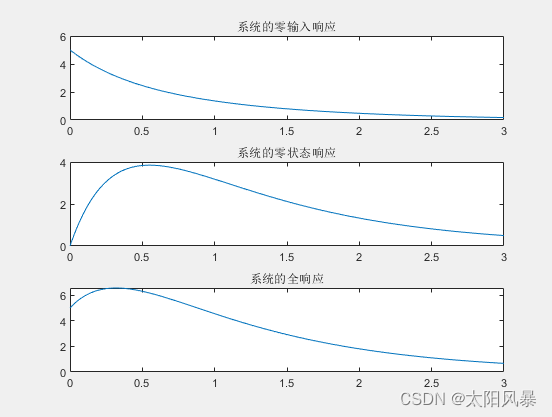
代码：

% 微分方程 y"(t) + 4y'(t) + 3y(t) = f'(t) + 2f(t)
% 输入信号 f(t) = 20e^(-2t)u(t) 
% 初始值 y(0^(-)) = 2, y'(0^(-)) = 1
% 求系统的零状态响应

a = [1 4 3];
b = [1 2];
[A B C D]=tf2ss(b,a);   %tf2ss函数将传递函数模型转化为状态空间模
sys=ss(A,B,C,D);        %sys由函数ss构造的状态空间模型
p=0.01;                 %定义取样时间间隔
t=0:p:3;                %定义时间范围

f=zeros(1,length(t))
zi=[1 2];
y1=lsim(sys,f,t,zi);     %系统的零输入响应
x=20*exp(-2*t);
y2=lsim(sys,x,t);        %系统的零状态响应
y3=lsim(sys,x,t,zi);     %系统的全响应
subplot(3,1,1);
plot(t,y1);
title("系统的零输入响应");

subplot(3,1,2);
plot(t,y2);
title("系统的零状态响应");

subplot(3,1,3);
plot(t,y3);
title("系统的全响应");

2、连续时间系统冲激响应和阶跃响应

题目&函数说明
已知 y’‘(t) + 2y’(t) + 3y(t) = f(t), 求系统的冲激响应和阶跃响应的时域波形

MATLAB 为用户提供了专门用于连续系统冲激响应并绘制其时域波形的impulse 函数。其函数 impulse()的调用格式：impulse(b,a)。其中 a 和 b 是由描述系统的微分方程左边和右边系数构成的两个行向量。
用于连续系统阶跃响应并绘制其时域波形的 step 函数。函数 step()的调用格式为：step(b,a)。其中 a 和 b 是由描述系统的微分方程左边和右边系数构成的两个行向量。

结果

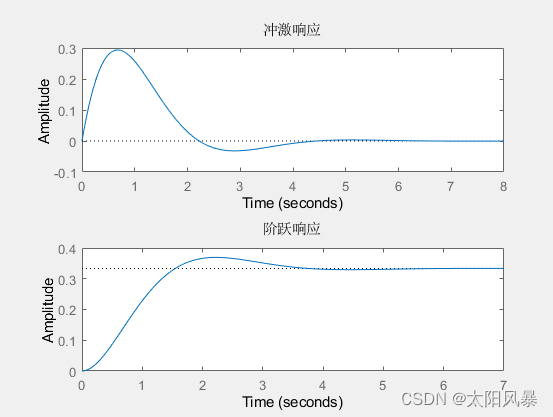
代码：

a=[1 2 3];
b=[1];
subplot(2,1,1)
impulse(b,a)
title("冲激响应")
subplot(2,1,2)
step(b,a)
title("阶跃响应")

3、卷积积分

题目&函数说明
计算两个指数信号 f₁(t) = e^-6t ， f₂(t) = e^-3t 的卷积
Matlab 的库函数 conv()只能计算离散序列 f1 与 f2 的卷积和，构造函数 conv() 实现两连续信号的卷积积分。
Y=conv(x,h)
实现 x,h 二个序列的卷积,假定都是从 n=0 开始，Y 序列的长度为 x，h 序列的长度两序列长度之和再减 1。
结果

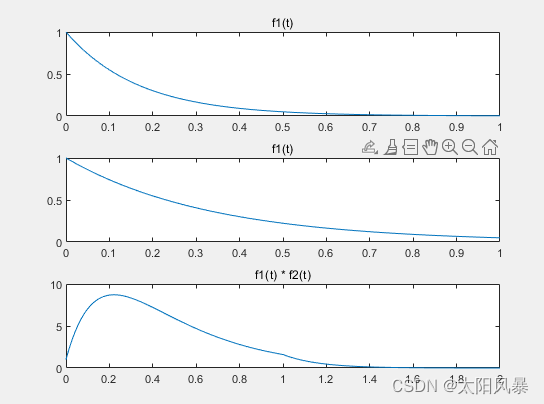
代码：

t=0:0.01:1;
y1=exp(-6*t);
y2=exp(-3*t);
y=conv(y1,y2);
l1=length(y1);

l2=length(y2);
l=length(y);
subplot(3,1,1);
plot(t,y1);
title("f1(t)");

subplot(3,1,2);
plot(t,y2);
title("f1(t)");

t1=0:0.01:2;
subplot(3,1,3);
plot(t1,y);
title("f1(t) * f2(t)");