一、LeetCode62. 不同路径

        1：题目描述（62. 不同路径）

        一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

        机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

        问总共有多少条不同的路径？

        2：解题思路

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        # 1：确认dp数组及含义
        # dp数组为二维数组，dp[i][j]表示，当前机器人走到[i][j]的位置有多少种不同的路径
        #:2：确认递推规则
        # 因为机器人每次只能向下或向右移动一步
        # 所以[i][j]的位置，是从[i-1][j]（[i][j]上面的位置）的位置向下走一步或[i][j-1]（[i][j]左面的位置）的位置向右走一步
        # 因此到达[i][j]的位置，是到达[i-1][j]和[i][j-1]路径的总和
        # dp[i][j] = dp[i-1][j] + dp[i][j-1]
        # 3：初始化
        # 第一行和第一列都需要初始化，因为[i][j]是从上面或者左面的位置过来的，需要知道上面和左面有多少种路径才能计算[i][j]位置有多少种路径
        # 4:遍历顺序，从左到右，从上到下
        dp = [[0 for _ in range(n)] for _ in range(m)]         
        # m表示有多少行，n表示有多少列
        for i in range(m):
            dp[i][0] = 1             # 初始化第一行的每个位置有多少种路径
        for j in range(n):
            dp[0][j] = 1             # 初始化第一列的每个位置有多少种路径
        print(dp)
        for i in range(1, m):        # 从上往下
            for j in range(1, n):    # 从左往右
                dp[i][j] = dp[i-1][j] + dp[i][j-1]     # 递推规则
        # 返回finish位置的路径方法总数
        return dp[m-1][n-1]

二、LeetCode63. 不同路径 II

        1：题目描述（63. 不同路径 II）

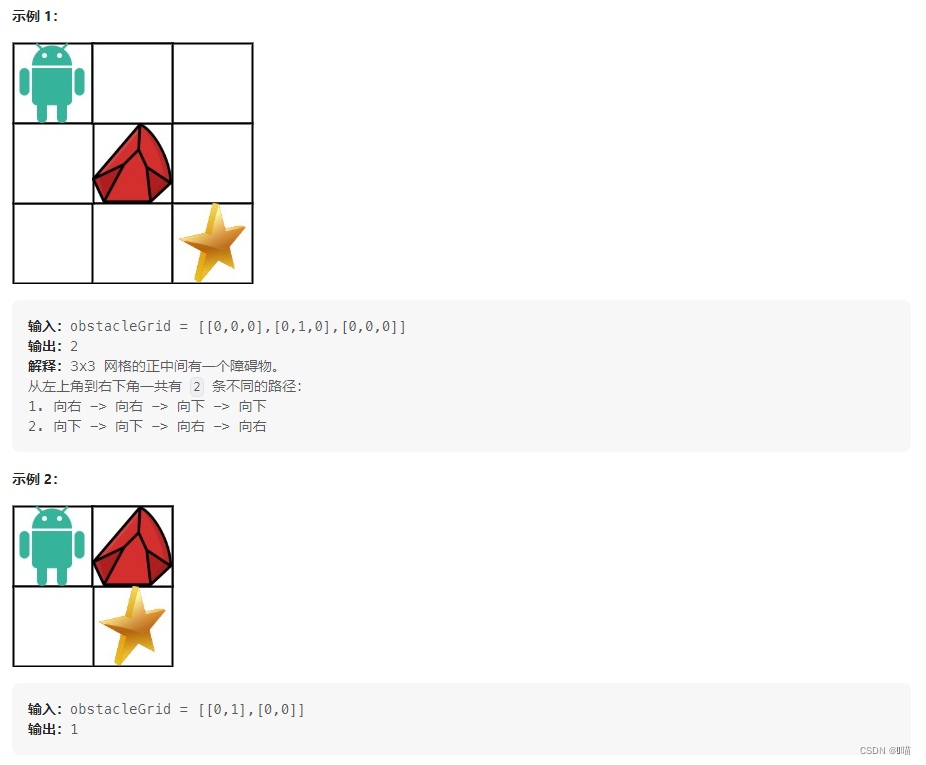
        一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

        机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

        现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

        网格中的障碍物和空位置分别用 1 和 0 来表示。

        2：解题思路

        跟上面62.不同路径差不多，需要注意以下两个点：

        第一个：递推规则，需要判断当前位置是否有障碍物，有障碍物就不能计算路径总和，没有障碍物才计算路径总和

        第二个：初始化，在第一行和第一列，碰到障碍物后，障碍物及其之后的位置，都不初始化了

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        # 1：确认dp数组及含义
        # dp数组为二维数组，dp[i][j]表示，当前机器人走到[i][j]的位置有多少种不同的路径
        #:2：确认递推规则
        # 因为机器人每次只能向下或向右移动一步
        # 所以[i][j]的位置，是从[i-1][j]（[i][j]上面的位置）的位置向下走一步或[i][j-1]（[i][j]左面的位置）的位置向右走一步
        # 因此到达[i][j]的位置，是到达[i-1][j]和[i][j-1]路径的总和
        # dp[i][j] = dp[i-1][j] + dp[i][j-1]
        # 3：初始化
        # 第一行和第一列都需要初始化，因为[i][j]是从上面或者左面的位置过来的，需要知道上面和左面有多少种路径才能计算[i][j]位置有多少种路径，当碰到障碍物，障碍物及后面的位置都不进行初始化了
        # 4:遍历顺序，从左到右，从上到下，当遍历的位置是障碍物时，不计算，继续遍历
        m, n = len(obstacleGrid), len(obstacleGrid[0])
        dp = [[0 for _ in range(n)] for _ in range(m)]          
        # m表示有多少行，n表示有多少列
        dp[0][0] = 1 if obstacleGrid[0][0] != 1 else 0
        if dp[0][0] == 0: return 0  # 如果第一个格子就是障碍，return 0
        for i in range(1,m):
            if obstacleGrid[i][0] == 1:
                break                # 遇到障碍物，直接退出循环，右面的就都不用初始化了
            dp[i][0] = 1             # 初始化第一行在障碍物之前的每个位置有多少种路径
        for j in range(1,n):
            if obstacleGrid[0][j] == 1:
                break                # 遇到障碍物，直接退出循环，右面的就都不用初始化了
            dp[0][j] = 1             # 初始化第一列在障碍物之前的每个位置有多少种路径
        for i in range(1, m):        # 从上往下
            for j in range(1, n):    # 从左往右
                if obstacleGrid[i][j] != 1:     # 当前位置，不是障碍时，计算当前位置有多少种路径
                    dp[i][j] = dp[i-1][j] + dp[i][j-1]     # 递推规则
                # 当前位置是障碍时，不计算当前位置有多少种路径，直接遍历下一个位置
        # 返回finish位置的路径方法总数
        return dp[-1][-1]