文章目录
- 文档配套视频讲解链接地址
- 第03章 树
- 3.1 二叉树创建
- 1. 实例20 二叉树创建
- 3.2 二叉树遍历
- 1. 二叉树的遍历
- 2. 三种遍历算法
- 3. 实例21 二叉树的遍历
文档配套视频讲解链接地址
- 腾讯课堂视频链接地址 : 24_树与二叉树_树的理解
- 腾讯课堂视频链接地址 : 25_树与二叉树_二叉树遍历
第03章 树
3.1 二叉树创建
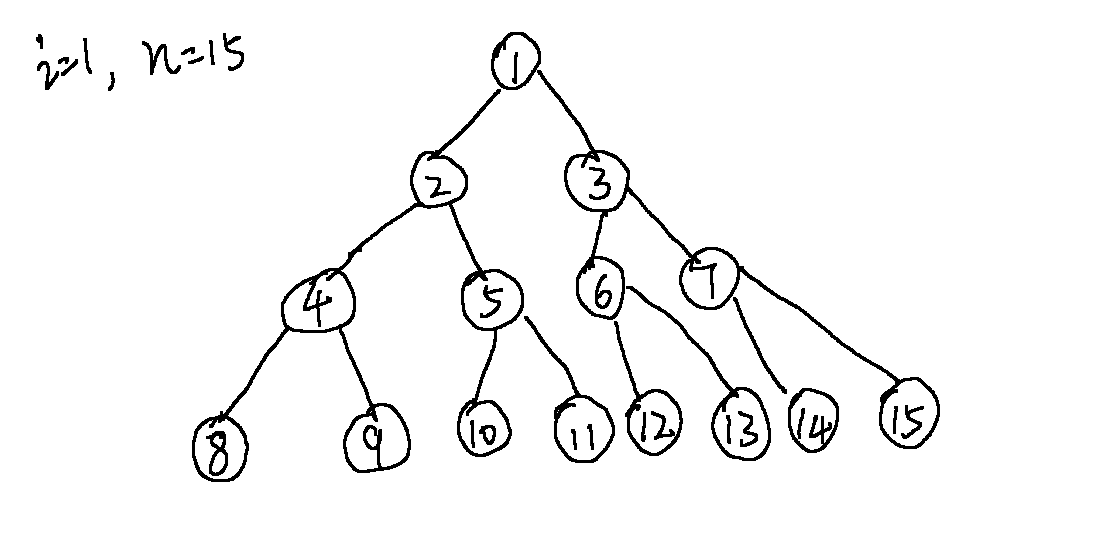
1. 实例20 二叉树创建
- 源文件
04-ds/20-bitree.c
- 源代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct node
{
int data;
struct node * lchild; // left child 左孩子指针
struct node * rchild; // right child 右孩子指针
}bitree_t;
// i :根的起始编号, n :要创建节点的个
// 根节点从1 开始
// n 表示的一共的节点个数
bitree_t * create_bitree(int i , int n)
{
bitree_t * r = malloc(sizeof(bitree_t));
r->data = i; // 创建根节点
printf("i=%d\n",i);
if(2*i <= n) // 有左孩子
{
r->lchild = create_bitree(2*i,n);
}
else
{
r->lchild = NULL; // 左孩子为空
}
if(2*i+1 <=n) // 有右孩子
{
r->rchild = create_bitree(2*i+1,n);
}
else
{
r->rchild = NULL;
}
return r;
}
int main(int argc, char const *argv[])
{
bitree_t *R = create_bitree(1,15);
return 0;
}
- 运行结果
i=1
i=2
i=4
i=8
i=9
i=5
i=10
i=11
i=3
i=6
i=12
i=13
i=7
i=14
i=15
3.2 二叉树遍历
1. 二叉树的遍历
-
遍历 :沿某条搜索路径周游二叉树,对树中的每一个节点访问一次且仅访问一次。
-
“遍历”是任何类型均有的操作,对线性结构而言,只有一条搜索路径(因为每个结点均只有一个后继),故不需要另加讨论。而二叉树是非线性结构,每个结点有两个后继,则存在如何遍历即按什么样的搜索路径进行遍历的问题。
2. 三种遍历算法
-
由于二叉树的递归性质,遍历算法也是递归的。三种基本的遍历算法如下 :
-
先序序列:访问顺序,根左右 ,先访问树根,再访问左子树,最后访问右子树;
-
中序序列:访问顺序,左根右: 先访问左子树,再访问树根,最后访问右子树;
-
后序序列:访问顺序,左右根,先访问左子树,再访问右子树,最后访问树根;
-
例如,
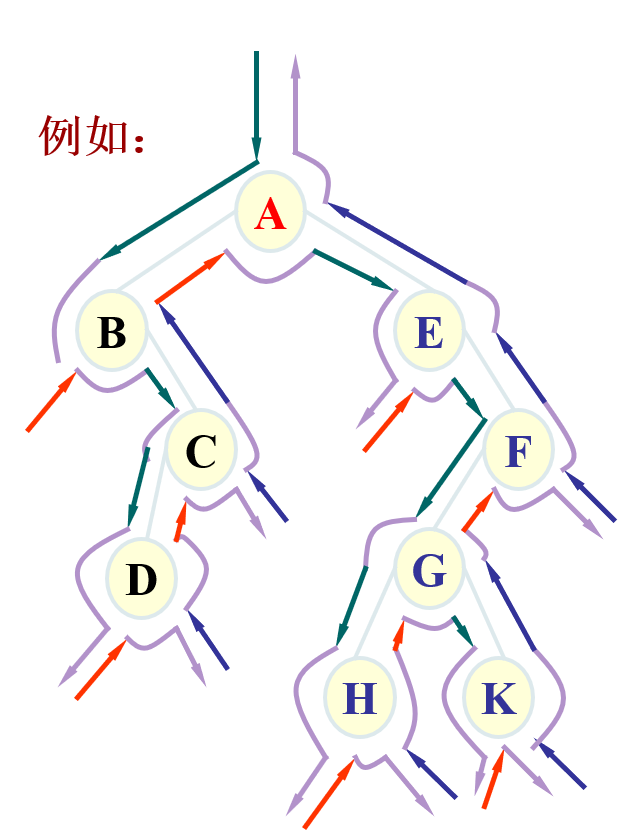
先序访问:先访问根, 再访问左, 最后访问右
A B C D E F G H K
中序访问: 先访问左, 再访问根, 最后访问右
B D C A E H G K F
后序访问: 先访问左, 再访问右 , 最后访问根
D C B H K G F E A
3. 实例21 二叉树的遍历
- 在实例20 的基础上实现遍历

- 先序顺序: 根左右
1 2 4 8 9 5 10 11 3 6 12 13 7 14 15
- 中序顺序: 左根右
8 4 9 2 10 5 11 1 12 6 13 3 14 7 15
- 后序顺序: 左右跟
8 9 4 10 11 5 2 12 13 6 14 15 7 3 1
- 源文件
04-ds/21-bitree.c
- 源代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct node
{
int data;
struct node *lchild; // left child 左孩子指针
struct node *rchild; // right child 右孩子指针
} bitree_t;
// i :根的起始编号, n :要创建节点的个
// 根节点从1 开始
// n 表示的一共的节点个数
bitree_t *create_bitree(int i, int n)
{
bitree_t *r = malloc(sizeof(bitree_t));
r->data = i; // 创建根节点
printf("i=%d\n", i);
if (2 * i <= n) // 有左孩子
{
r->lchild = create_bitree(2 * i, n);
}
else
{
r->lchild = NULL; // 左孩子为空
}
if (2 * i + 1 <= n) // 有右孩子
{
r->rchild = create_bitree(2 * i + 1, n);
}
else
{
r->rchild = NULL;
}
return r;
}
// 递归函数一定要有结束条件
// 根左右
int preorder(bitree_t *b)
{
// 结束条件 空树返回
if (b == NULL)
return 0;
// 先访问根
printf("%d ", b->data);
// 再访问左
preorder(b->lchild);
// 最后访问右
preorder(b->rchild);
return 0;
}
// 中序访问
// 左根右
int inorder(bitree_t *b)
{
// 结束条件 空树返回
if (b == NULL)
return 0;
// 访问左
inorder(b->lchild);
// 访问根
printf("%d ", b->data);
// 访问右
inorder(b->rchild);
return 0;
}
// 后序访问
// 左右根
int postorder(bitree_t *b)
{
// 结束条件 空树返回
if (b == NULL)
return 0;
// 访问左
postorder(b->lchild);
// 访问右
postorder(b->rchild);
// 访问根
printf("%d ", b->data);
return 0;
}
int main(int argc, char const *argv[])
{
bitree_t *R = create_bitree(1, 15);
printf("先序顺序:");
preorder(R);
printf("\n");
printf("中序顺序:");
inorder(R);
printf("\n");
printf("后序顺序:");
postorder(R);
printf("\n");
return 0;
}
- 运行结果
先序顺序:1 2 4 8 9 5 10 11 3 6 12 13 7 14 15
中序顺序:8 4 9 2 10 5 11 1 12 6 13 3 14 7 15
后序顺序:8 9 4 10 11 5 2 12 13 6 14 15 7 3 1