题目描述：

有 A 和 B 两种类型的汤。一开始每种类型的汤有 n 毫升。有四种分配操作：

提供 100ml 的汤A 和 0ml 的汤B 。
提供 75ml 的汤A 和 25ml 的汤B 。
提供 50ml 的汤A 和 50ml 的汤B 。
提供 25ml 的汤A 和 75ml 的汤B 。
当我们把汤分配给某人之后，汤就没有了。每个回合，我们将从四种概率同为 0.25 的操作中进行分配选择。如果汤的剩余量不足以完成某次操作，我们将尽可能分配。当两种类型的汤都分配完时，停止操作。

注意不存在先分配 100 ml 汤B 的操作。

需要返回的值：汤A 先分配完的概率 + 汤A和汤B 同时分配完的概率 / 2。返回值在正确答案 10-5 的范围内将被认为是正确的。

示例 1:

输入: n = 50
输出: 0.62500
解释:如果我们选择前两个操作，A 首先将变为空。
对于第三个操作，A 和 B 会同时变为空。
对于第四个操作，B 首先将变为空。
所以 A 变为空的总概率加上 A 和 B 同时变为空的概率的一半是 0.25 *(1 + 1 + 0.5 + 0)= 0.625。

示例 2:

输入: n = 100
输出: 0.71875

提示:

0 <= n <= 10^9
添加链接描述

解题思路一：动态规划，这里将所有的汤除了25，缩小数值。自底向上

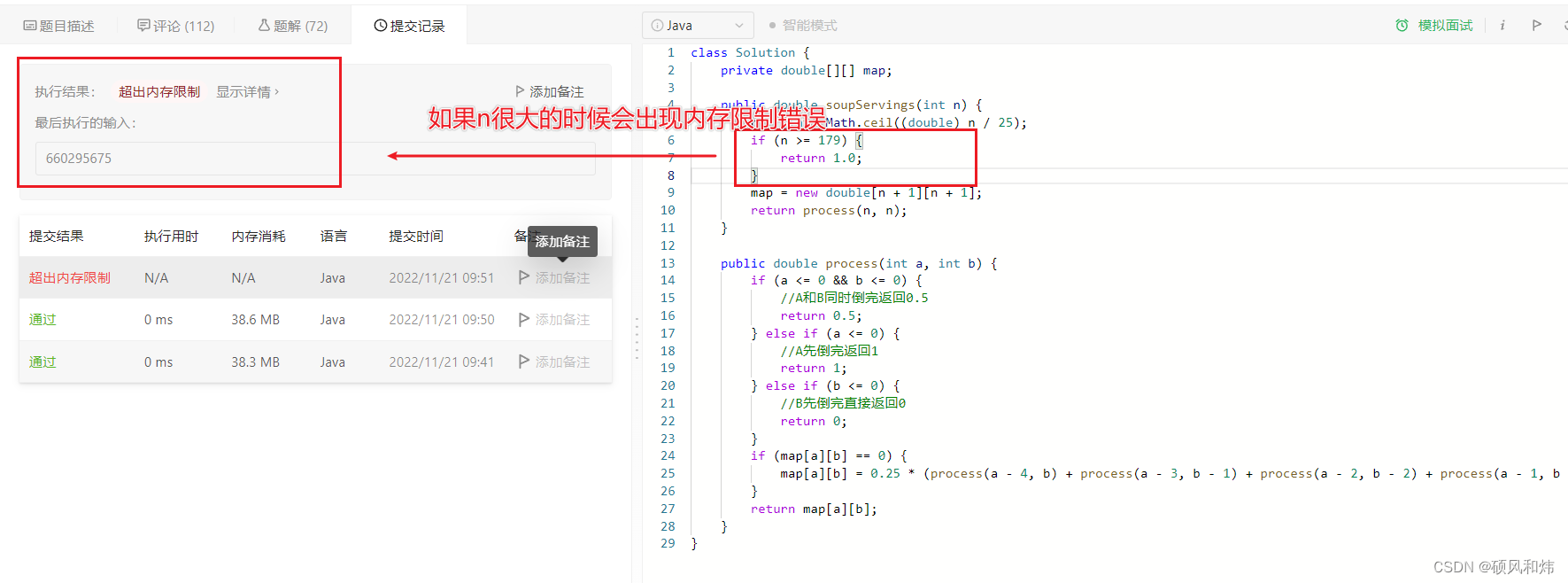
在n非常大的时候A先被取完的概论非常接近1（计算期望），因此计算发现在 n≥179×25时，我们只需要输出 1.0 作为答案即可。
在n较小的时候用动态规划。

class Solution {
public:
    double soupServings(int n) {
        n=ceil((double)n/25);
        if(n>=179) return 1.0;
        vector<vector<double>> dp(n+1,vector<double>(n+1));
        dp[0][0]=0.5;//AB同时分完的概率为1.0，A先分完的概率为0，所以概率为1.0*0.5=0.5
        for (int i=1;i<=n;++i) dp[0][i] = 1.0;//此时AB同时分完的概率为0，A先分完的概率为1，所以概率为1.0
        for (int i=1;i<=n;i++)
            for (int j=1;j<=n;j++)
                dp[i][j]=(dp[max(0,i-4)][j]+dp[max(0,i-3)][max(0,j-1)]+dp[max(0,i-2)][max(0,j-2)]+dp[max(0,i-1)][max(0,j-3)])/4.0;//对有减操作的需要保证大于等于0
        return dp[n][n];
    }
};

在这里插入图片描述

时间复杂度：O(n^2)
空间复杂度：O(n^2)
当n>=179
时间复杂度：O(1)
空间复杂度：O(1)
那么综合：
时间复杂度：O(C^2)
空间复杂度：O(C^2)
C=179。

解题思路二：记忆化搜索，自顶向下搜索，会减少许多无效状态的计算。

class Solution {
public:
    vector<vector<double>> memo;
    double soupServings(int n) {
        n=ceil((double)n/25);
        if(n>=179) return 1.0;
        memo=vector<vector<double>>(n+1,vector<double>(n+1));
        return dfs(n,n);//递归实现
    }
    double dfs(int a, int b) {
        if(a<=0&&b<=0) return 0.5;//AB同时分完          
        else if(a<=0) return 1;//A先            
        else if(b<=0) return 0;//B先
        if(memo[a][b]>0) return memo[a][b];
        memo[a][b]=0.25*(dfs(a-4,b)+dfs(a-3,b-1)+dfs(a-2,b-2)+dfs(a-1,b-3));
        return memo[a][b];
    }
};