【POJ No. 2431】 丛林探险 Expedition

北大OJ 题目地址

【题意】

一群人开着一辆卡车冒险进入丛林深处，卡车油箱坏了，每走1米就会漏1升油，他们需要到最近的城镇（距离不超过106米）修理卡车。卡车当前位置和城镇之间有N （1≤N≤104 ）个加油站，每个加油站都可以加油1～100升，卡车油箱容量没有限制。目前卡车距离城镇L 米，有P 升油（1≤P ≤106 ）。

他们希望在前往城镇的路上尽可能少地停下加油，请给出到达城镇所需的最少加油次数。

【输入输出】

输入：

第1行包含单个整数N ，表示加油站的数量。第2…N +1行，每行都包含两个整数，用于描述加油站，第1个整数是从城镇到加油站的距离，第2个整数是该加油站的可用油量。第N +2行，每行都包含两个整数L 和P 。

输出：

输出到达城镇所需的最少加油次数。若无法到达城镇，则输出-1。

【样例】

【思路分析】

若在可以到达的距离范围内有多个加油站，则将这些站点的加油量入队（优先队列）。若走到下一个加油站之前油会耗尽，则需要加油（优先队列中最大加油量）后继续走，当油量大于或等于卡车到城镇的距离L 时结束。

【举个栗子】

在输入样例中，卡车距离城镇25米，有10升油。沿着这条路，距离城镇4、5、11和15米有4个加油站（可求出这些加油站距离卡车21、20、14和10米），这些加油站可分别提供多达4、2、5、10升的油。

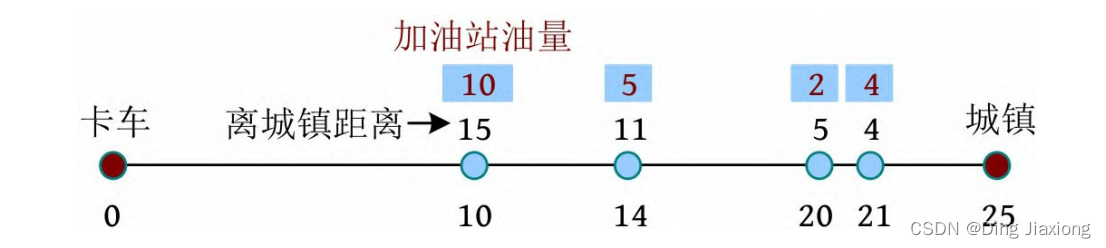
求解的过程：因为卡车有10升油，所以首先开车10米，在第1个加油站加油10升，在第2个加油站加油5升，油箱的油量累计可到达距离25，可直接开车到镇上。

∴ 答案：停靠2次。

【算法设计】

① 按照距离降序排序。

② 初始化。加油次数ans=0，当前可到达的位置pos=P ，第k 个站点k =0。

③ 若pos<L ，则执行第4步；否则结束，输出答案。

④ 若可到达的位置超过第k 个加油站，则将第k 个站点的加油量入队（最大值优先），k ++，一直循环到不满足条件为止。

⑤ 若队列为空，则输出-1；否则加油（pos+=que.top();que.pop();ans++），转向第3步。

【算法实现】

#include<cstdio>
#include<queue>
#include<algorithm>

using namespace  std;

#define N 10005

int n , L, P;

struct node{
	
	int dis , add; //距离；可加油量 
	
}port[N];

bool cmp(node a , node b){
	
	return a.dis > b.dis; //按距离降序 
}

void solve(){
	
	priority_queue<int>que;
	
	//ans：加油次数； pos：当前可到达的位置 k ：第k 个加油站
	int ans = 0, pos = P , k = 0;
	
	while(pos < L){
		
		while(pos >= L - port[k].dis && k < n){
			que.push(port[k].add);
			k ++;
		}
		
		if(que.empty()){
			
			printf("-1\n");
			return ;
		}
		else{
			
			pos += que.top();
			que.pop();
			
			ans ++;
		}
	} 
	printf("%d\n" , ans);
} 

int main(){
	
	while(~scanf("%d" , &n)){
		
		for(int i = 0 ; i < n  ; i++){
			
			scanf("%d %d" , &port[i].dis , &port[i].add);
		}
		
		scanf("%d%d" , &L , &P);
		sort(port, port + n ,cmp);
		
		solve();
	}
	return 0;
}