1.复杂度分析原则

1.1 最大循环原则

只看高阶部分

public class SumNum {
    public static void main(String[] args) {
        System.out.println(sum2(4));
    }
    /**
     * 1-n 的累加
     * @param n
     * @return
     */
    public static int sum1(int n){
        int sum = 0;// 执行1次
        for (int i=0;i<n;i++){//这是三个代码 分别执行1 n n 次
            sum+=n;//执行n次
        }
        return sum;
        //这边算一下这个这串代码累计执行的时间 T(n) = (3n+2)*Timer(单位时间)
        //这边的时间复杂度   O(3n+2)   O(n)
    }

    public static int sum2(int n){
        int sum = 0;// 执行1次
        for (int i=0;i<n;i++){//这是三个代码 分别执行1 n n 次
            for (int j=0;j<n;j++){//分别执行n n² n²
                sum+=i*j;//执行n²
            }
        }
        return sum;
        //这边算一下这个这串代码累计执行的时间 T(n) = (3n²+3n+2)*Timer(单位时间)
        //时间复杂度   O(3n²+3n+2) O(n²)
    }
}

如果代码里面有n 和 n² 那么就只看高阶

1.2 加法原则

 public static int sum3(int[] n,int [] m){
        int sum = 0;
        for (int i : n){
            sum+=i;
        }

        for (int i : m){
            sum+=i;
        }
        return sum;
    }
    //这边的复杂度就是适用加法原则
    //时间复杂度O(m+n) ,但是依然是O(n)的一种

1.3 乘法原则

两个n 相互调用的话，这串代码就是O(n²)

 public static int sum1(int n){
        int sum = 0;// 执行1次
        for (int i=0;i<n;i++){//这是三个代码 分别执行1 n n 次
            sum+=sum5(i);//执行n次
        }
        return sum;
        //这边算一下这个这串代码累计执行的时间 T(n) = (3n+2)*Timer(单位时间)
        //这边的时间复杂度   O(3n+2)   O(n)
    }

    public static int sum5(int n){
        int sum = 0;// 执行1次
        for (int i=0;i<n;i++){//这是三个代码 分别执行1 n n 次
            sum+=n;//执行n次
        }
        return sum;
        //这边算一下这个这串代码累计执行的时间 T(n) = (3n+2)*Timer(单位时间)
        //这边的时间复杂度   O(3n+2)   O(n)
    }

2.常见复杂度

常数	O(1)
线性	O(2)
对数	O(log n)
线性对数	O(n log n)
k次方	O(nᴷ)
指数	O(2ᴺ)
阶乘	O(n!)

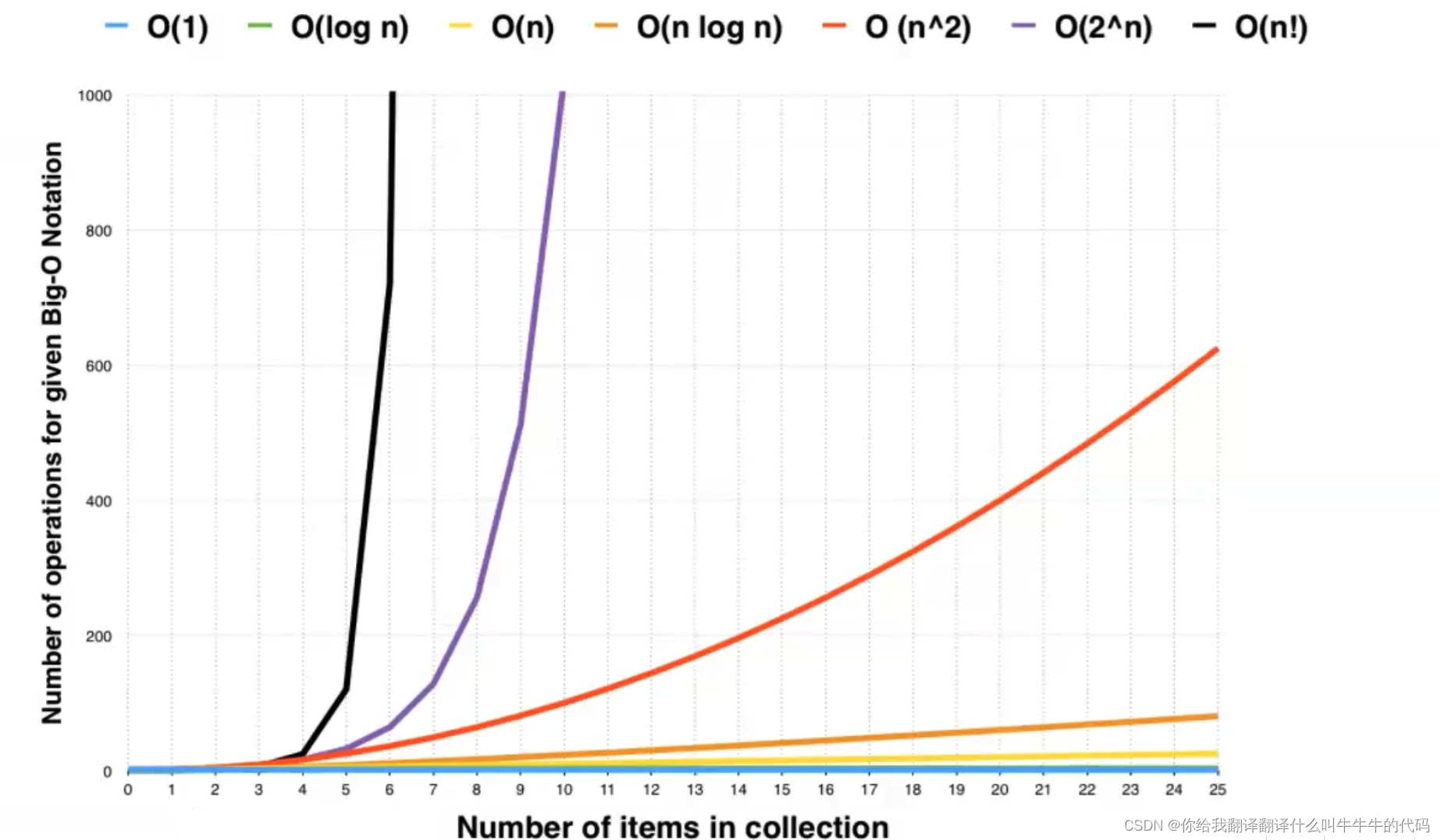
x 轴为要处理的数据量，y是花费时间。可以看出来阶乘的写法是花费时间最高的（所以不一定非要删库对吧😊）

2.1 O(1)

常数复杂度其实就是和数据量没多大关系举个例子,虽然这个集合数据量增大，但是我的时间却和数据量没多大关系。

public void handlerData(List datas){
        System.out.println(datas.size());
    }

2.2 O(n)

这个是我们平常工作中做常见的复杂度

public void handlerData2(List datas){
       for(Object item : datas){
           System.out.println(item.toString());
       }
    }

2.3 O(log n)

简单点说就是执行次数肯定比n 少

public void handlerData3(List datas){
        for(int i=0;i<datas.size();i++){
            System.out.println(datas.get(i*2));
        }
        //这边会执行多少次肯定不是 n次
        //2ᴷ = n；
        //n = log₂ᴷ
    }