Python学习----面向对象

news2025/1/11 15:03:34

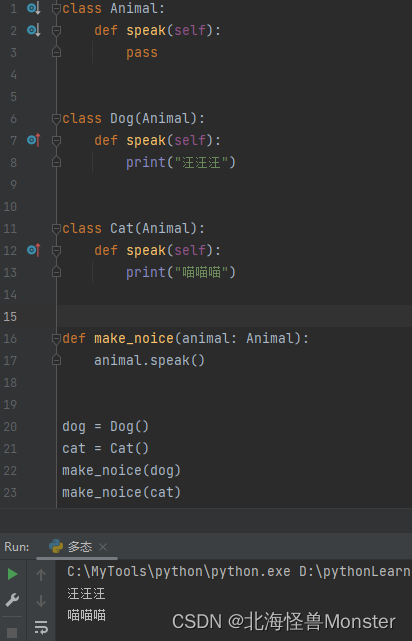
面向对象思想就不说了，和java一样。这是为了自己能够一直看教程不走神做得笔记。

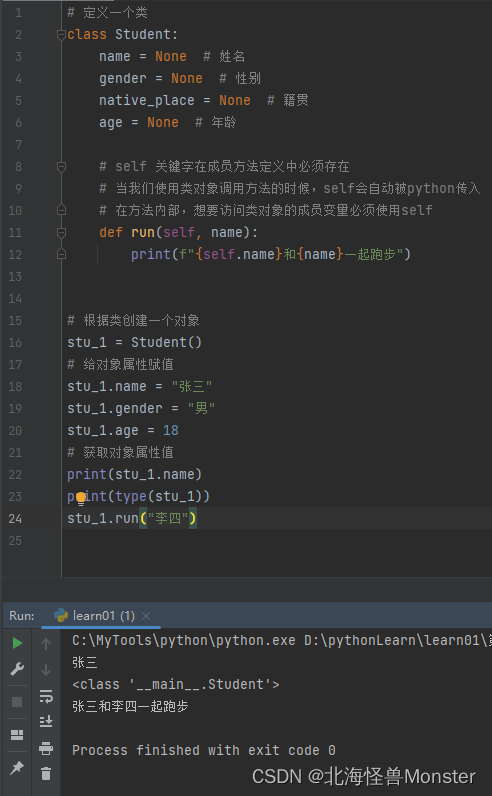
类的定义和赋初值

成员变量和成员方法，含义和java一样。
成员变量的申明没啥好记得
需要关注得是成员方法，在定义成员方法得时候，需要传入self关键字，这个就相当于java得this关键字。但是python需要在定义得时候手动传入，根据前面教程分析，要是你在成员方法内部直接使用name变量，python一定会认为你在成员方法内重新定义了一个name变量，所以使用self关键字来进行区分。没办法，这是python语法得特点。
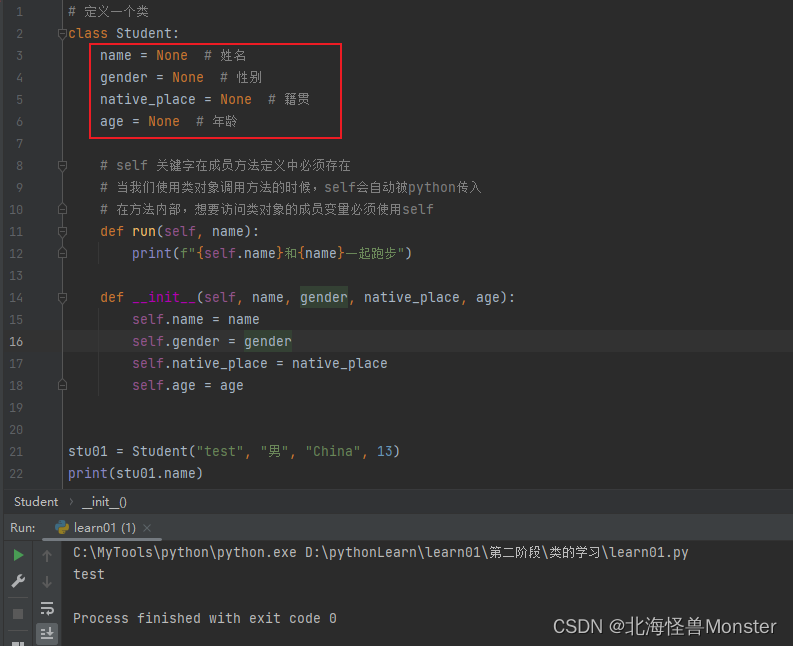
在这里插入图片描述

构造方法

下图标记得成员变量可以不写，在你 init方法中给成员变量赋值得时候，如果你写了，就是赋值操作。
如果你不写，就是定义加赋值操作
在这里插入图片描述

魔术方法

内置得类方法称为，魔术方法。有很多，学习几个常见得

__init__    构造方法
__str__     字符串方法
__lt__   小于，大于符号比较
__le__  小于等于、大于等于符号比较
__eq__  == 符号比较

str方法

打印变量名，默认是打印对象内存地址。重写 str 方法可以更改
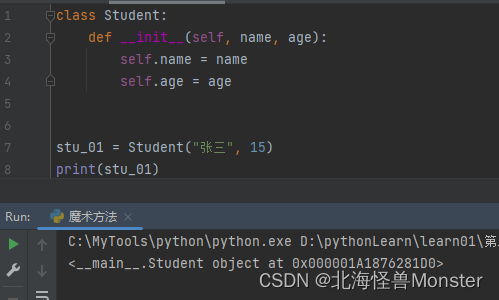
在这里插入图片描述
但是需要注意得是，str 这个方法需要返回值

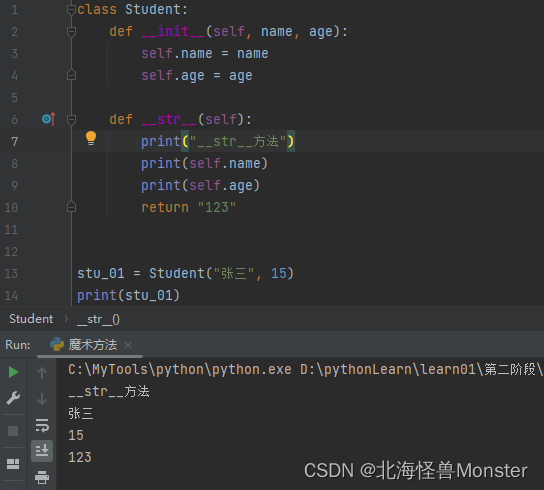
要是没有返回值就会报错

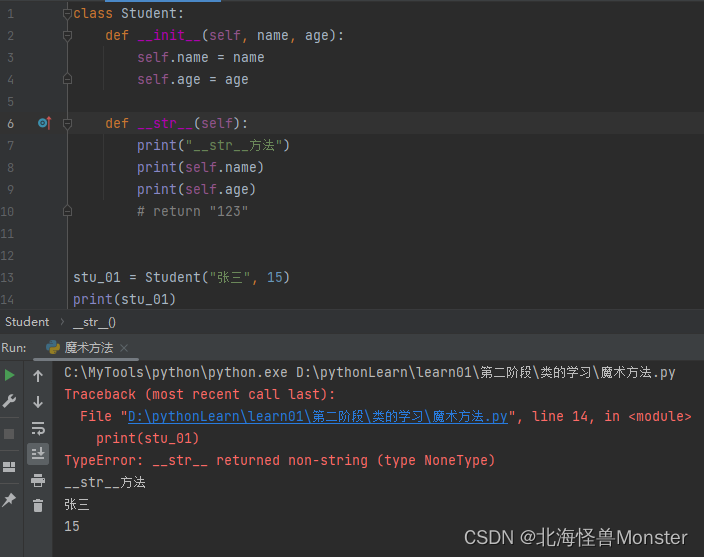
lt 小于符号比较方法

在没有重写魔术方法直接使用会报错
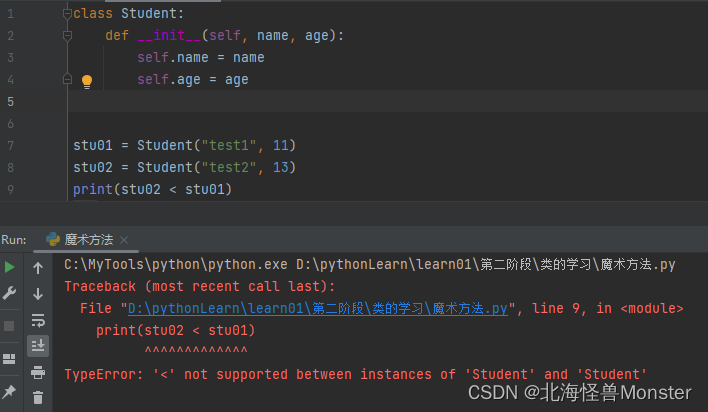
在这里插入图片描述
直接对2个对象进行比较是不可以得，但是在类中实现 lt 方法，即可同时完成小于符号和大于符号两种比较
自己定义对象之间比较得规则
传入参数： other 另一个类对象
返回值：布尔类型
比较规则：自己定义

对于小于等于和大于等于需要重写 le 方法。重写方式和 lt 是一样得
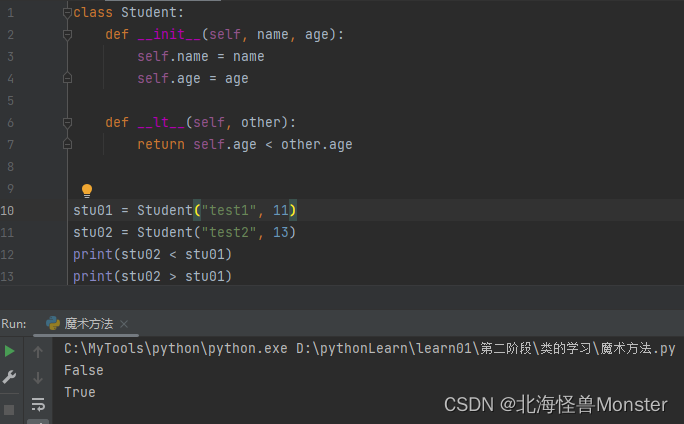
在这里插入图片描述

eq 相等比较运算

如果没有重写 eq 方法，两个类对象名字使用 == 是比较内存地址是否相等，永远是都返回 False
在这里插入图片描述

封装

封装、继承、多态

刚才在定义成员方法和成员变量这些操作，就是在进行封装。

私有成员变量，私有成员方法定义
对比 java真的很简单，只需要在成员变量或者成员方法前面加两个下划线，就说明这个成员是私有得

和java一样只要是私有得，就不能直接通过类对象进行直接访问
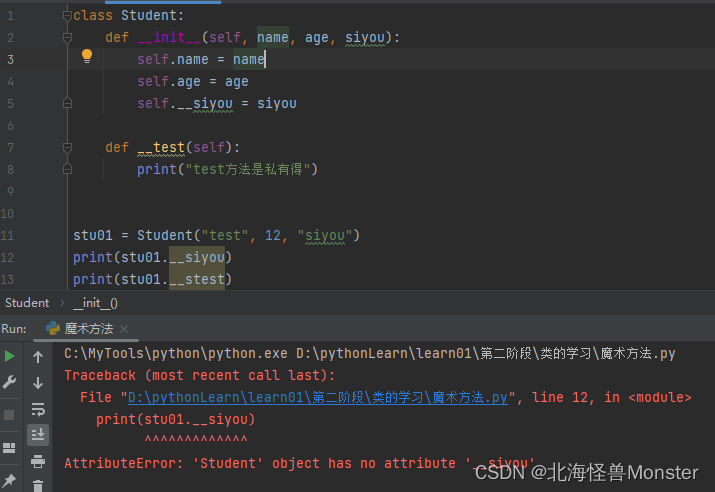
在这里插入图片描述
同理，和java一样，需要通过其他方法进行访问

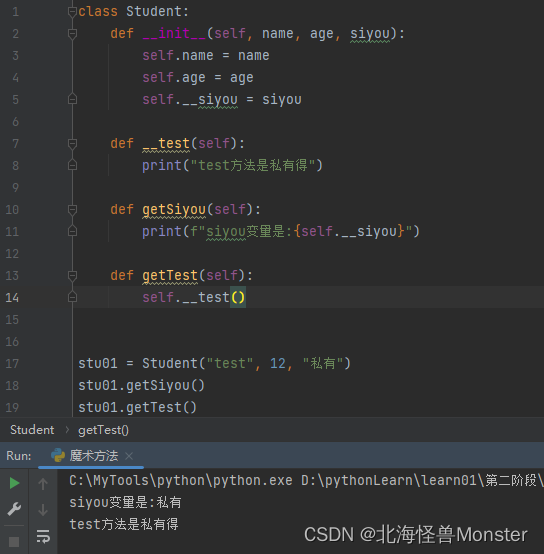
继承

单继承
语法： class 子类(父类)
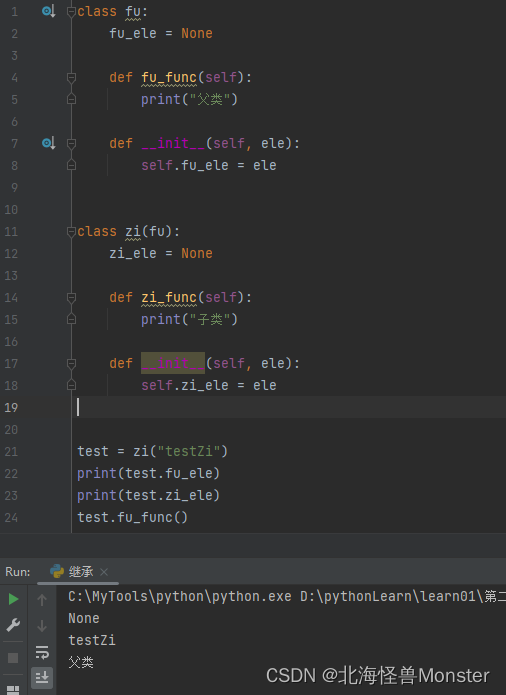
在这里插入图片描述
多继承
语法： class 子类(父类1，父类2…)
如果父类中有成员同名，那么优先继承左边得，谁先出现谁优先级高。

如果子类中没有新功能，使用pass关键字替代。
在这里插入图片描述

复写

子类复写父类中得成员，在子类中重新定义同名得属性或方法
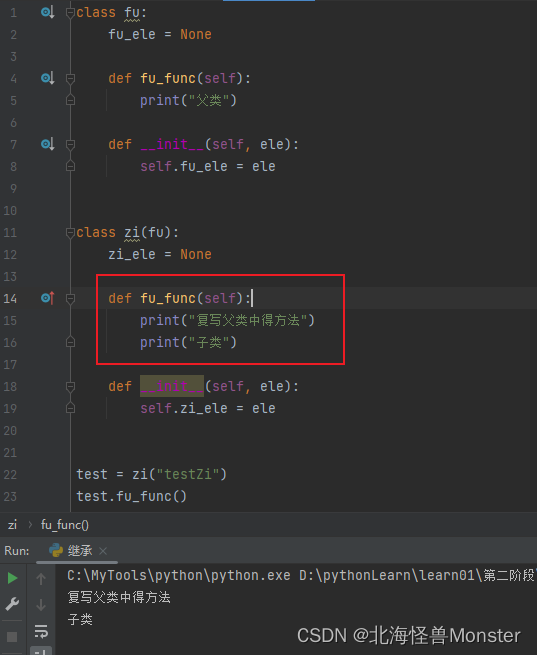
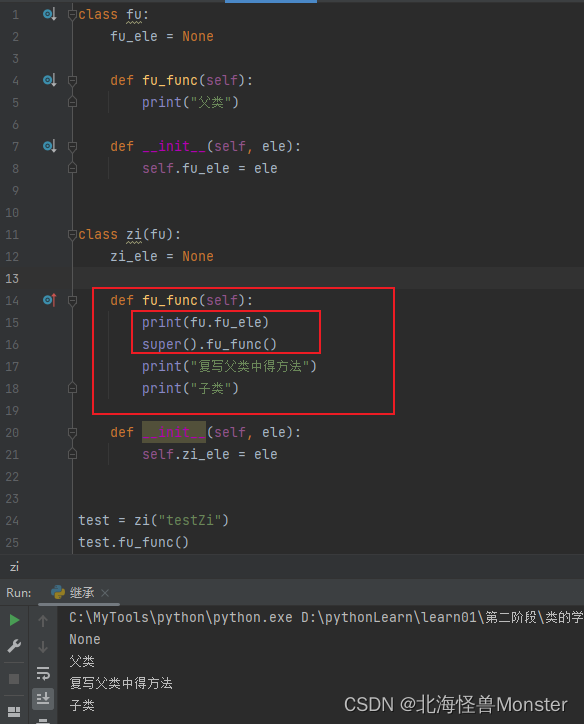
在这里插入图片描述
在子类中调用父类成员：
方法1 ：super().成员变量 super().成员方法()
方法2 ：父类名.成员变量父类名.成员方法(self)

在这里插入图片描述

类型注解

当我们调用方法，进行传参时， ctrl + p 弹出提示
如下图：当我们调用系统方法时，会有提示传什么类型参数，但是自己定义得函数调用时，是没有类型提醒得。
在这里插入图片描述
Python在3.5版本之后引入类型注解，以方便编辑器提示，也方便开发者对参数类型进行注解
只是一个备注，不影响程序运行。

变量的类型注解：

# 变量类型注解--------------------------------
# 1、告诉编辑器这个变量时什么类型
# 2、也方便以后开发工作
# 基础类型注解
var_1: int = 10
var_2: str = "test"
var_3: bool = True
# 类对象类型注解
test_zi: zi = zi()
# 基础容器注解
my_list: list = [1, 2, 3]
my_tuple: tuple = (1, 2, 3)
my_dict: dict = {"key": 11}
# 容器类型详细注解
my_list2: list[int] = [1, 2, 3]
my_tuple2: tuple[int, str, bool] = (1, "test", True)
my_dict2: dict[str, int] = {"key", 12}

# 注释类型注解---------------------------------------
var_01 = 10  # type: int
my_list01 = [1, 2, 3]  # type: list
my_dict02 = {"key", 12}  # type:dict[str:int]

类型注解并不会真正对类型做验证和判断，你要是标记为int ，但是实际传入得时str ，是不会报错的。

函数和方法的类型注解：
对参数的类型注解

def test_func(x: int, y: int):
    return x + y

对返回值的类型注解
def 函数名(形参…) -> 返回值类型

def test_func(x: int, y: int) -> int:
    return x + y

Union类型注解
例如：当集合中出现多种类型数据
my_list = [1,2,“test”,True]
Union[str, int, bool] 表示这个list里面要么是 str ，要么是 int ，要么是 bool

from typing import union 
my_list: list[Union[str, int, bool]] = [1,2,"test",True]
my_dict: dict[str,Union[str, int]] = {"name":"test","age":13}

# 同样方法形参和返回值也使用
def func(data: Unoin[int,str]) -> Union[int,str]:
	pass

多态

类型注解就是在为Python的多态做准备。
在之前的学习中，方法的形参是不需要著名类型的。现在通过类型注解来注明类型，但是这个也不是强制性的。
在类型注解中，有学习到 pass 关键字。其实这个勉强对应java的接口。通过这两个条件，就可以形成Python的多态。
总的含义还是和java一样：父类接收子类

多态：同一个行为，使用不同的对象获得不同的状态
抽象类：含有抽象方法的类
抽象方法：方法体是空实现(pass)的方法
在这里插入图片描述