正交试验法设计测试用例

正交试验法设计工具：

1、正交设计助手

2、AllPairs

3、python（本质是使用AllPairs）

先看一个案例：

假设一个web系统，需要做兼容性测试，该系统兼容不同操作系统、数据库和web服务器软件，并且客户端有许多的浏览器：

>浏览器：Firefox、IE、Google Chrome
>数据库：MySQL、Oracle、DB2
>应用服务器：nginx、Apche、Tomcat
>操作系统：Windows Server、Unix、Linux

分析

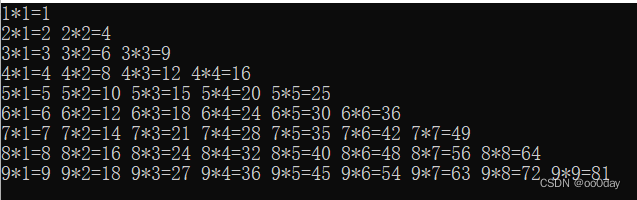
4因素3水平实验：全面实验需要81条用例，而正交实验只需要9条用例

全面实验：
$$3^4=81$$
正交实验：
$$L_9(3^4)$$

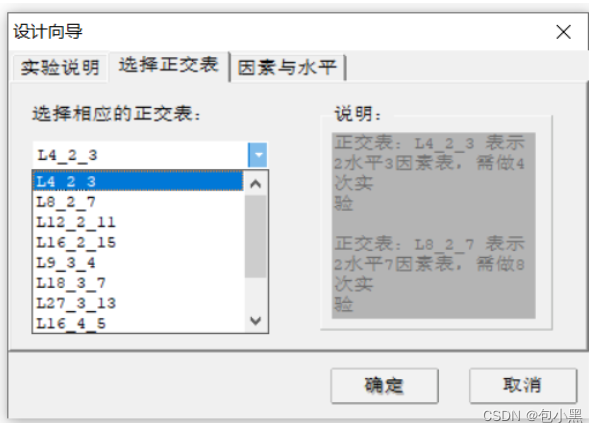
工具一>正交设计助手

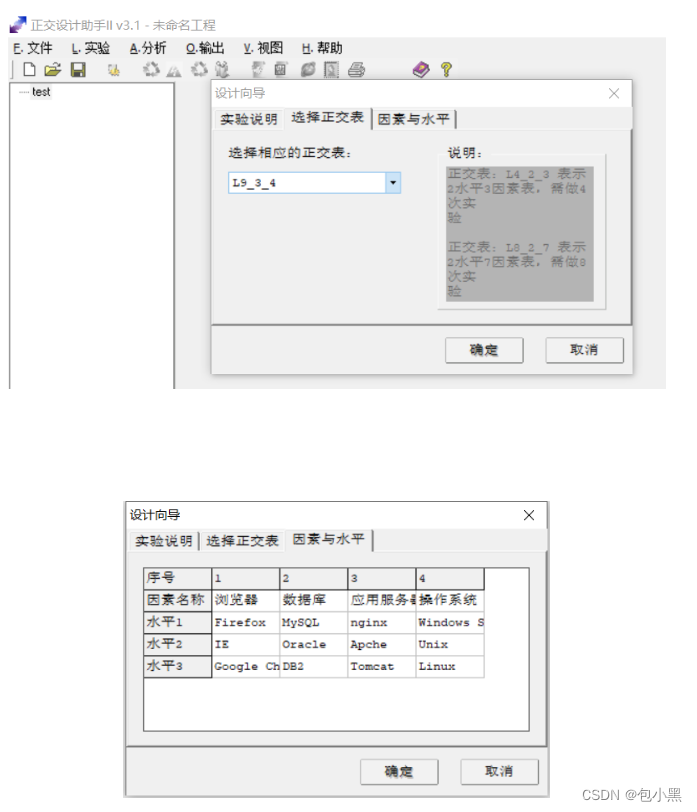
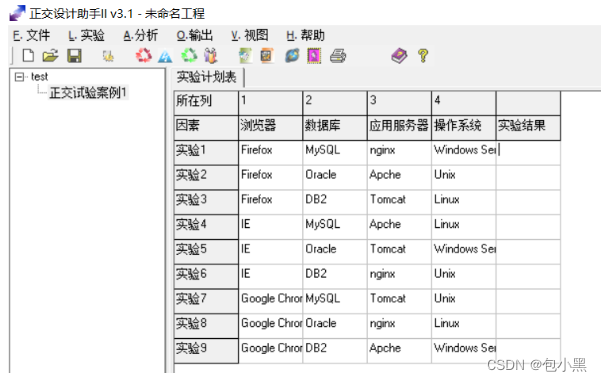
工具二—>Allpairs

1、根据需求在Excel中确定因素及每个因素的取值（水平）

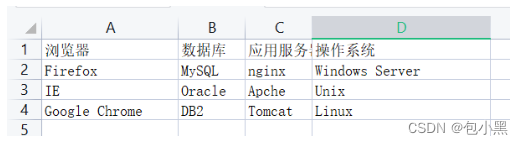
2、新建txt文档，将取值表数据直接复制粘贴到txt中，并保存

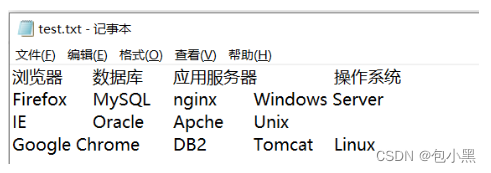
3、将步骤2的文件放到Allpairs安装的文件路径下

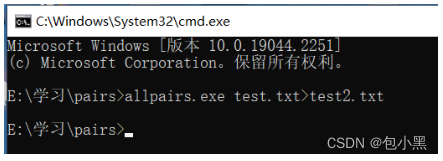
4、打开cmd命令行工具，进入Allpairs解压后所在的路径，

输入allpairs.exe test.txt>test2.txt，然后回车

6、打开Allpairs文件路径，就可以看到新生成的正交表文件test2.txt了

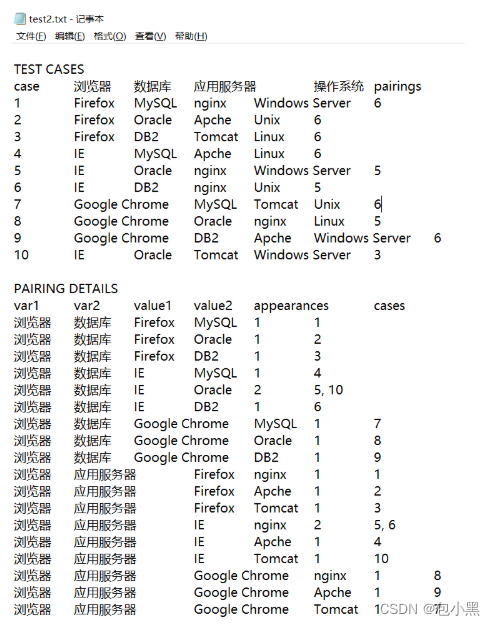
就是不知道为什么Allpairs生成的用例多了一条，可能是我下载的版本问题

如果因素和水平符合标准的正交表，建议使用正交设计助手，如果水平没有那么规范，建议使用Allpairs

工具三—>python

from allpairspy import AllPairs
 
parameters = [
    ["Firefox", "IE","Google Chrome"],
    ["MySQL", "Oracle", "DB2"],
    ["nginx", "Apche", "Tomcat"],
    ["Windows Server", "Unix", "Linux"]
]
 
print("测试用例:")
for i, pairs in enumerate(AllPairs(parameters)):
    print("用例编号{:2d}: {}".format(i+1, pairs))